已知协方差矩阵求特征值_矩阵分析-期末复习笔记（下）

复习笔记的上篇在这里：

辰晞：矩阵分析-期末复习笔记（上）​zhuanlan.zhihu.com

目录：

1. 特征值，特征向量，相似 (Eigenvalues, eigenvectors, similarity)
2. 酉相似 & 酉等价 & 正规矩阵 (Unitary similarity & unitary equivalence & normal matrices)
3. Jordan标准型，LU分解 (Jordan canonical form, LU factorization)
4. Hermitian矩阵，相合 (Hermitian matrices, Congruences)
5. 向量范数 & 矩阵范数 (Vector norms, matrix norms)
6. Gersgorin圆盘 (Gersgorin discs)
7. 正定矩阵 & 半正定矩阵 & 极分解 & 奇异值分解 (Positive definite & semidefinite & polar decomposition & SVD)
8. 正矩阵 & 非负矩阵 (Positive / nonnegative matrices)

---

5. 向量范数 & 矩阵范数 (Vector norms, matrix norms)

向量范数：Vector norms

• 定义：一个向量范数（
  ）应该满足以下几个条件：
  • 1 - 非负性 Nonnegativity:
    • 1a - 正定性 Positivity:
      if & only if
  • 2 - 齐次性 Homogeneity:
  • 3 - 三角不等式 Triangular Inequality:
• 只满足1, 2, 3 但不满足1a的范数称为 prenorm.

内积：Inner product

• • 定义：
    应该满足以下几个条件：
    • Nonnegativity:
      • Positivity:
        if & only if
    • Additivity
    • Homogeneity
    • Hermitian Property
• 有用的推论：平行四边形不等式（necessary & sufficient）

Cauchy-Schwarz柯西不等式

• • 不等式相等：x, y线性相关

几个重要的向量范数：

• norms:
  • p<1时：不再是norm，不满足三角不等式
• : "Manhattan norm" - 等于各项绝对值相加
• : Euclidean length
• :

向量范数的分析性质：

• 数列收敛 Convergence of a sequence
  • 定义：a sequence
    (of vectors in
    ) converges to a vector
    with respect to
    if & only if
    可以写作：
    .
  • 如果数列关于一个范数的极限存在，那么这个极限是唯一的。
  • 同一个数列关于不同的范数的极限可以不一样。
• Comparability
  • are positive, called comparability constant
  • 推论：for finite dimensional vector spaces,
    with respect to
    if & only if
    with respect to
  • For finite dimensional real / complex vector spaces, all norms are equivalent.
• 柯西数列 Cauchy sequence
  • 通俗的定义：一个数列中在去掉有限个元素后，可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正数。
  • 严谨的定义：给定数列
    ，对于
    ，存在正整数
    使得
    ——我们叫这个数列为Cauchy sequence with respect to this norm
    .
  • 数列
    收敛于V中的一个向量 if & only if 这个数列是一个柯西数列，with respect to a norm
    in vector space V.
• （这整个analytic的部分我都很虚，因为没正紧学过analysis，学起来比较吃力。非常期待下学期，终于可以开始上正式的analysis课了。）

向量范数的几何意义：

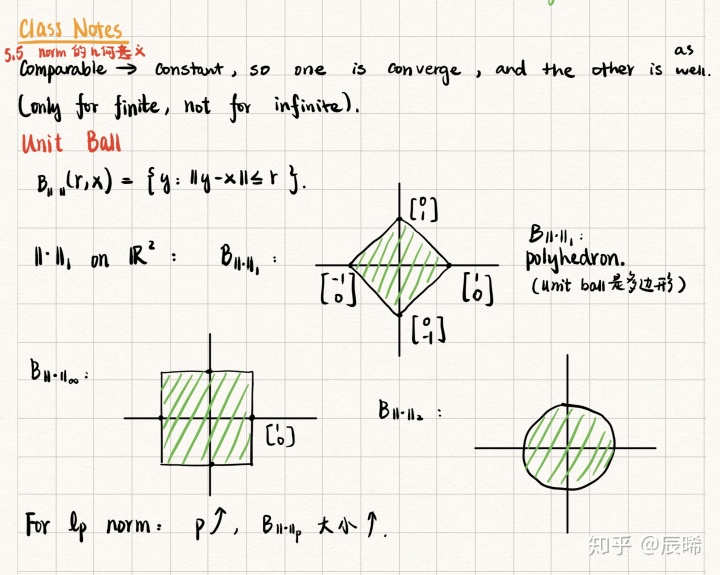
Matrix Norm 矩阵范数

• 定义打起来比较费劲，为了省事直接附笔记：

• 注意这里比矩阵范数多了一条Submultiplicative property（图上第四条），因为矩阵可以和矩阵相乘，而向量乘起来只能用内积，不能直接乘。
  • 从这一条也可以推出下面的三条：

与向量范数相似，我们也可以定义

矩阵范数：

• p = 1:
  = largest absolute column sum of A
• p = 2:
  = largest spectral radius of A
• p =
  :
  = largest absolute row sum of A.

向量范数与矩阵范数的相容 Compatible matrix norm

• 在向量范数上定义矩阵范数：
• 相容：
  • 存在矩阵范数和向量范数
    ，对于任意A, x都有：
    ，则我们称矩阵范数
    和向量范数
    相容。
• 对于每个矩阵范数，都存在和它相容的向量范数。
• 可用
  证得
  .
  • 时，
    converges to 0.

Condition number

• measures the closeness of the least-square approximation.
  • high condition number: magnifies err
• 如果奇异值都靠近，则是一个好的approximation。

矩阵范数与可逆

• 如果存在矩阵范数
  使得
  ，则矩阵A是可逆矩阵。
• 这种情况下，A的逆矩阵可以表示为：

---

6. Gersgorin圆盘 (Gersgorin discs)

Gersgorin圆盘

• 定义：对一个n*n的矩阵，把每行的去心绝对和
  当作直径，对角元当作圆心，可以画n个圆盘。特征值就在这些圆盘中。

• 证明：

• There are as many eigenvalues in each connect component as there are discs.
  • 如果k个圆盘连在一起，那么它们的集合就包含了k个特征值。
• 可以通过圆盘来估计特征值
  • 如果圆盘不包含(0,0)，则这个矩阵可逆。
  • 因为A和A转置特征值一样，所以除了row disk，我们还可以考虑column disk。
  • 相似前后特征值不变，所以我们也可以对A做对角相似：
    , where D is a diagonal matrix. 这样可能可以缩短一些圆盘的半径（但会不可避免的扩大某些别的圆盘的半径。）
  • 如果是实矩阵+圆盘互不相交，则特征值都是实数
    • （如果特征值是复数，则有conjugate pair，圆盘无法互不相交）

可约/不可约矩阵 Reducible & Irreducible matrices

• Permutation similarity:
  ，如果能通过这种变换得到一个左下角的reducing block，则这个矩阵是可约的。
  • 一个n-by-n的矩阵的reducing block，是p-by-q的（p+q = n）
• 如果我们画出矩阵的directed graph：
  • 不可约矩阵：strongly connected，且
    (it's a positive matrix)
• 如果矩阵的图是strongly connected, then
  is not an eigenvalue of A unless
  lies on the boundary of every disc.
  • 这种情况下：特征向量的每个项绝对值相等。特征值几何重数=1.
• 不可约 + 对角优势(diagonal dominant)：
  • 如果一个矩阵是irreducible & diagonal dominant, with at least one strict diagonal dominant, 那么这个矩阵可逆。

---

7. 正定矩阵 & 半正定矩阵 & 奇异值分解 (Positive definite & semidefinite & SVD)

• 定义：通过quadratic forms定义（只适用于Hermitian矩阵，一个矩阵要先是Hermitian，才能讨论它正定与否——我老是忘这个前提）
  • 正定矩阵 positive definite：
  • 半正定矩阵 positive semidefinite：
  • 同理，也有negative (semi)definite & indefinite
• 如果一个矩阵正定（括号内：半正定），则：
  • 特征值都是大于（等于）0的实数 - （因为Hermitian矩阵特征值都是实数）
    • 正定的A是可逆的
    • 正定的A，Gersgorin圆盘都在y轴右侧
  • 所有的principal submatrices都为（半）正定 - （可以从interlacing推出）
  • trace, det, principal minors 都大于（等于）零
    • 所以，正定的A一定有LU分解
  • 如果A是半正定：
    • tr(A) = 0 if & only if A = 0.
    • if & only if
• Congruence: 相合前后正定性不变
  • 所有的正定矩阵A都可以写成
    ，B是可逆矩阵。
    • 原因：特征值>0, congruence to identity
• （半）正定的A存在square root:
  ，这个square root也是（半）正定的。
• 正定矩阵 + 正定矩阵，得到的也是正定矩阵
• 正定矩阵
  正定矩阵，得到的不一定是正定矩阵。（可能根本都不Hermitian）
  • 但如果得到的是Hermitian的，那就是正定的

极分解 Polar Decomposition

• :
  , with 正定的P和酉矩阵U.
• General case: 也适用于非square的矩阵：此时的P是半正定，U有orthonormal columns.
• 求极分解：
  ，所以
  ，然后可以倒回去求U.
• 同理，我们也可以换位：
  ，V是酉矩阵，Q为正定矩阵
  • 求这种极分解时，把AA*变成A*A就行了。
• 极分解有点像数字中的极坐标系，把一个数字写成
  （r是正数，
  在单位圆上）。在A=PU中，P是正定矩阵（像正数），U是酉矩阵（也像个单位圆）。

奇异值分解 - Singular Value Decomposition

• 在general case的极分解中，可以把半正定的P酉对角化：
  ，这样，就能把A分解成：酉矩阵 乘 对角矩阵 乘 酉矩阵。
• 我们把D中的元素叫做A的奇异值：singular values
  ，它们都是非负实数（因为P的特征值都为非负）。
• 求奇异值 = 求A*A 或 AA*的特征值，再开方。
• A的奇异值的乘积 =
• 求奇异值分解：
  • 的(i,i) position: A的奇异值
    （从大到小排列，奇异值不够0来凑）
  • : 从左到右按奇异值的顺序排列normalized的、A*A的特征向量
  • :
    (
    分别是U和V的
    column)
• 奇异值也可以有interlacing，像特征值一样。

Hadamard积 - Hadamard Product

• 定义：entry-wise multiplication,
• 两个（半）正定的矩阵的Hadamard积也为（半）正定。——普通的乘积可不一定，都不一定Hermitian.
  • Hadamard product preserves Hermisity.
• Haramard-wise多项式：
  • p(t) sends positive number to positive number：如果A是（半）正定，那么
    也是（半）正定矩阵。
• 最大奇异值 largest singular value:

同时对角相合 - Simultaneously diagonalized by congruence

• 如果A正定，B是Hermitian，那么A, B can be simultaneously diagonalized by congruence.
  • In this event, the congruence matrix C can be taken so that
    with identity
    and diagonal
• Hermitian的A, B都不是正定的也不要紧，如果一个A和B的linear combination是正定的，那他们也可以simultaneously diagonalized by congruence.

Loewner partial order

• 定义：
  • : A 是正定矩阵
  • : A 是半正定矩阵
  • : A-B是正定矩阵
  • : A-B是半正定矩阵
• 若A,B都为正定，
  ，则有：
  • if and only if
  • If A succeq B
    , then
    for all k in increasing/decreasing order.
• 若A为正定，B为半正定，则：
  • if & only if
• Congruence不改变这个ordering:
  • If
    , then
• Hadamard:
• 以上几条的证明：

关于determinant的不等式 - Determinantal Inequality

• Hadamard不等式
  • 对于正定矩阵A：
  • It's an equality if & only if A is diagonal
  • 推论：对于半正定矩阵B with column or row
    ：
• Fisher不等式
  • 对于正定矩阵P：
    ， 有：
• Koteljanskii不等式
  • 对于正定矩阵A，有：

---

8. 正矩阵 & 非负矩阵 (Positive / nonnegative matrices)

非负矩阵的分类（从“严”到“松”）：positive -> primitive -> nonnegative & irreducible -> nonnegative

• 正矩阵 Positive matrices:
  , all entries are positive.
• 本原矩阵 Primitive matrices:
  , 且存在
  for some power k.
  • primitive matrices are also irreducible
• 非负&不可约矩阵 nonnegative & irreducible: 可以是primitive的，也可以不是primitive的。

Perron定理: 正矩阵, positive matrices:

2. --spectral radius is one eigenvalue of A.
3. 作为特征值，有一个所有元素都是正的左or右特征向量 (x>0)。
4. 's algebraic multiplicity = geometric multiplicity = 1. （代数重数=几何重数=1）
5. If
6. converges to a rank-one matrix:
7. If B is a principal submatrix of A:
8. For some small
   ,
   . （
   只有(i,j)元素是1，其他都是0）

Perron定理的推广: 本原矩阵, primitive matrices:

• 正矩阵的1~7条 still hold for primitive matrices.
• 原因：primitive matrices have some power that are positive. Reducing from
  ，1~7条中的性质都在。
• We treat primitive matrices like positive matrices.

推广: 不可约的非负矩阵, nonnegative & irreducible matrices:

• 1~4 都和正矩阵一样
• 5:
  ——这里可以有等于的情况。实际上，如果有多个特征值绝对值等于spectral radius，它们都会被evenly placed on the spectral circle.
• 6. no longer converges.
• 7 & 8: still hold.

推广: 非负矩阵, nonnegative matrices(到这一步，基本就不剩下什么了):

2. still holds
3. 作为特征值，有一个所有元素都是非负的左or右特征向量 (
   )。
4. no longer holds——代数重数、几何重数都可以比1大。

• 从上边第3条推出的一个重要推论：Positive, primitive, irreducible matrices只能有一个positive eigenvector (不算它的multiple的话)。
  • 原因：别的特征值的特征向量和它点乘起来要等于0 (biorthogonality)，特征向量又不能为0，所以别的特征向量一定会有某些元素为负数。

判断一个矩阵是否为primitive：

• 首先，primitive和非0元素的大小没有关系，只和“元素是不是0”有关系
• 判定方法：画出directed graph，数simple cycle的个数，找最大公约数(gcd: greatest common divisor)
  • gcd(cycle length) = 1 if & only if a matrix is primitive.
  • 推论：如果一个矩阵是irreducible & nonnegative，如果它有至少一个正的对角元，那它就是primitive的。（因为gcd(1, anything) = 1）
  • 这里的gcd也是number of eigenvalues on the spectral circle.
• Critical component:
  • 是一个“极限”的power: 一个irreducible矩阵如果过了这个幂还不是正的，就永远不可能是正的了。
• 对于任意非负矩阵A，估计spectral radius:
  • min row sum
    max row sum

（完）

（再次祝我final考好><！）