数学物理方法pdf_数学物理中的一些重要方法和结论（随时补充）

1、求和必同质

这是我最想强调的一个点，数学和物理中都有体现。在数学上能够求和的东西必然属于同一个空间（这样才能定义加法），直和也不例外。当然这句话可以进行一定拓展：同一线性方程中的所有未知量都属于同一空间并具有相同性质，这里的空间不做严格定义，大家应该能明白意思，之所以拓展也是可以根据和的性质推出。

举个简单的例子：

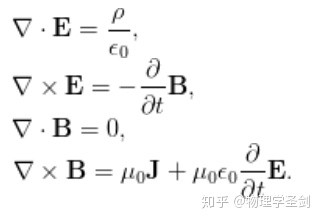
这是真空中麦克斯韦方程组的微分形式，我不需要知道矢量算符的含义就能判断1式左边运算结果是标量，若把2式移项，则移项后右边的0代表0向量而非数字0（为什么要区别已经解释过了，另外矢量对时间的偏导仍为矢量）。

矩阵的本征方程

右边的0是数字0而非零矩阵，因为左边行列式的运算结果是数量。

实积分的结果不可能是复数，因为积分本质上是无穷求和。

对于有无穷存在的情况，允许不同阶无穷的量进行求和但高阶的无穷小可以忽略，所以有效部分的无穷阶数也相同（这一点在学极限时尤为重要）。

在物理中，多项式每一项量纲必然相同，借此可以简单的判断一些物理量的量纲，如量子力学连续性方程中

是概率密度，量纲很好判断，

算子是空间一阶微商算子，作用于

后量纲除以一个距离量纲。对时间的偏导显然是除以一个时间量纲。求和项量纲相同，则概率流密度矢量

的量纲就是

的量纲除以一个时间量纲再乘一个距离量纲。

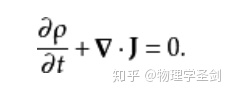
2、量纲分析

既然说到量纲就谈一下量纲分析，量纲分析其实很简单，无非就是物理量的量纲作为乘因子参与代数运算，初中生都会，只是有一些需要注意的地方。

导数对量纲的影响相当于除法，这从导数的定义很容易看出（微商嘛），积分呢也很简单，积分的本质是求和，求和必同质因此结果的量纲就是积分元的量纲，也就是被积函数的量纲乘以后面微元的量纲（微分对量纲无作用）。对于一些矢量运算只需要看它的分量式或标量式即可。

sin cos e指数 ln 等等的超越函数，内部一律为没有量纲的数量。如

中，E是能量量纲，则

整体无量纲，可以很容易的计算出玻尔兹曼常量k的量纲，热力学中kT往往一同出现作能量量纲。偶尔会有lnM（M有量纲）这样的东西出现，放心，它绝对不是单独出现的，后面一定有-lnm（m与M同量纲）或者整理方程使只有一个ln时内部无量纲。解释也很简单，以

为例，其麦克劳林展式为

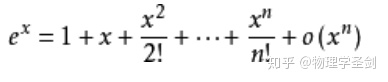
其中1为无量纲的数量，若x有量纲，仅看前两项就发现这与求和必同质相矛盾。这里正好提一下量子力学里的指数算符，量子力学里常有形如

（H为有量纲算符）的算符，它是用展开式进行定义的，其展开式第一项的1只能理解为单位算符而不能理解为数字1，若H化为矩阵形式，则第一项变为单位阵E。所以依然符合求和必同质的要求。

另外量纲虽然是一个物理概念，却有其数学合理性。举例来说：勾股定理是

，能不能是

；为何球的表面积正比于半径的平方而体积是三次方，这些存粹的数学问题只需要引入一个长度量纲就很容易回答。量纲是一个数量本身的性质，当同一种数量形成一个空间时，量纲就成为类似于基矢量的一个属于这个空间的特征量，对于标准化的线性空间，基矢量即是单位矢量，我想这大概能解释为什么把量纲也叫做单位了。

事实上我们也确实可以用线性空间定义量纲运算，同一空间（同种量纲）内只允许加法和数乘，而不同量纲的乘法需要重新定义，最方便的方法就是直积，比如

，这里

必须理解为毛与毛的直积，是一个新量纲的符号而已，和数的平方并没有什么关系，除法也可以用乘逆元解直积来定义。

3、对称性

对称性这个东西可以说是数学物理中最最最重要的方法之一了，要是详细讲的话十篇文章恐怕也不够，因此在这里只简单讲几个对称性的应用让大家感受一下。

首先必须强调的是，对称性绝对不是一个几何概念，因此当我们提到某种对称性不一定能够有某种几何图像来直观表达，对称性应当定义为：某一数学对象，在某种变换下不变。这个数学对象可以是方程，可以是矩阵，可以是几何体，什么都可以是，因此对称性是一个非常广泛的概念，应用自然很多。先介绍几个高中就能用到的例子：

一个数学对象

（啥都可以是），含有参量

，对其中任意量不同参量做变换

,

不变，称

具有

交换对称性。（那个括号表示对换）。比如式

,任意交换a，b，c中的两个，结果不变。

还是这个

和参量

，如果对这n个参量一起做变换

，结果不变，称

具有轮换对称性。（这个括号表示按此序列轮换）。比如矢量的混合积：

,做轮换

结果不变。

这两种对称性做高中和高数题特别方便。比如要证明一个很长的式子，但它具有其中一种对称性，那么可以把它拆成对称的几部分，接着证明其中的一个，剩下的可以根据对称性直接写出其形式。一个方程拥有几何图像，那么方程的对称性在图像里一定会体现，反之亦然。

还有，习题一般都是定解问题，即给定的条件完全决定了解空间的结构以及要求的解。如果给定的条件都具有某种对称性，那基本可以料定解也一定具有这种对称性。那有没有反例呢？有的，当条件都满足某种对称性，解却不满足时，我们说该对称性在这个问题中发生了破缺。不要一听到对称性破缺就发怵，定义已经告诉你了，就是这么简单一回事，并且，对称性破缺一定有破缺的原因。之所以在物理中有很多艰深的研究就是因为那些破缺的机制人们还没找到。

其实在高中我们就已经接触过对称性破缺了，比如奇偶性就是一种对称性，比如函数

是偶函数，在宇称（坐标反演）

下不变，其导函数（完全由

自身决定）却是奇函数，它满足的对称性是

在宇称和

联合变换下不变。究其原因，是我们在对

做宇称时，根据导数的定义：

很明显，对

来说，在

和

处所做的变换是不同的，这是个局域变换（随参数变化），而宇称应该是全局变换（对所有参数都相同）。所以表面上，

和

共用自变量

，对

反演应该是同一种变换，但其实这里我们是把他们当作了两个独立的函数，自变量之间也是独立的（取值不互相依赖），应该理解成

和

。可见，对称性破缺其实是人为因素造成的，就连物理中的对称性自发破缺，本质上应该也是存在一些我们没有意识到的机制，如果哪天意识到了，必然会惭愧地把“自发”二字去掉。

就是这么一个简单的例子，足以让我们解释量子力学中的一个重要规律：如果薛定谔方程

具有某种宇称（由势能

决定）,则其解

不一定具有该宇称，但一定具有宇称，所以对称势场的能量本征态通常是奇偶宇称交替出现的。原因就如刚才的例子，薛定谔方程是微分方程，而求导具有改变宇称的性质。

物理中还有一个很重要的对称性叫规范对称性，以后另写文章吧。从很多年前开始，理论物理前沿的研究（量子场论、弦论），就基本都是在玩作用量和对称性了。关于作用量和对称性有一个著名的noether定理，是说一切连续对称性必然导致一个守恒量（对时间），比如能量守恒对应时间平移不变，动量守恒对应空间平移不变，角动量守恒对应空间旋转不变……当然对称性远远不止这些，因此想做理论物理，不把张量、群论这些专门搞对称性的数学工具玩熟是不可能的。