画数轴的步骤_简单高次不等式的解法：数轴穿根法、猜根、多项式的竖式除法...

在高中数学的学习过程中有时候会接触到简单高次(一般为3次)不等式问题，本文就和大家一起来探讨一下，如何解简单高次不等式

一、该不等式所对应的多项式已经因式分解，能轻易知道其零点，如下题

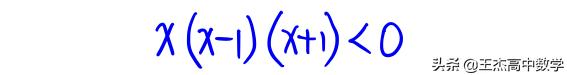
此种情况可以直接利用数轴穿根法

步骤1：先画数轴

步骤2：在数轴上标出零点

步骤3：开始穿根，若最高次项系数为正，则从右上方开始穿根，若最高次项系数为负，则从右下方开始穿根，画波浪线如下图所示【本题最高次项系数为正，所以从右上方开始】

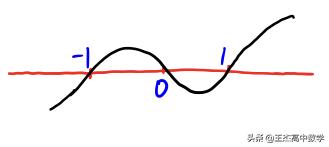
步骤4：读取解集，上正下负，所以本题的解为

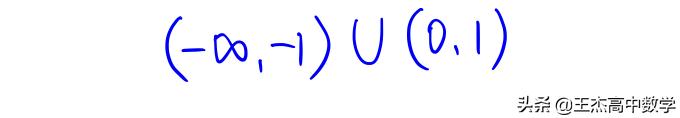
为了让大家能更直观的理解，请看下图【用作图软件画出的精确图形】，手绘的草图虽然不够精确，但是对该不等式最终的解是没有影响的

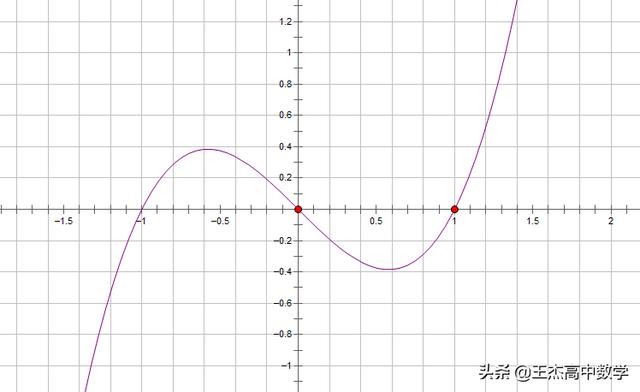
下面我们再看一个例题

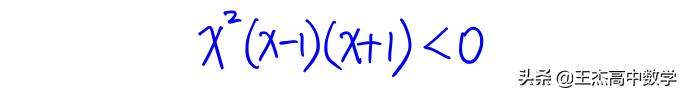
此例与上面那个题类似，但是该四次多项式的4个根中有两个相等的根“0”，那么是不是有所不一样呢？我们先看看用作图软件画出的精准图形，看看它所对应的四次函数图像长什么样吧！

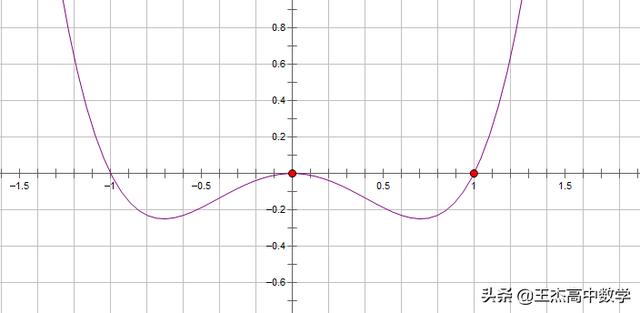
我们发现数轴穿根时，在“0”这个地方并没有穿过去，而是与数轴相切了，那么这是不是偶然现象呢！我们可以自己动手多做几个“实验”就知道了

【常见的函数画图软件有：几何画板(Windows版)，goodgrapher(ios版)，desmos(ios版)，mathlab图形计算器(安卓版)等等，有兴趣的同学可以自己动手试试看】

相信聪明的你在自己操作之后应该找出了其中的规律：奇穿偶切

如果某个根的个数为奇数，则画波浪线时要在该根处穿过数轴

如果某个根的个数为偶数，则画波浪线时在该根处不穿过数轴，即与数轴相切

在掌握此规律后我们再做此类题就应该很轻松了，比如

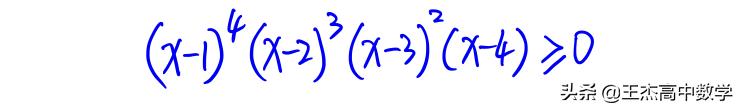
你能在草稿纸上画出它的大致图像吗？

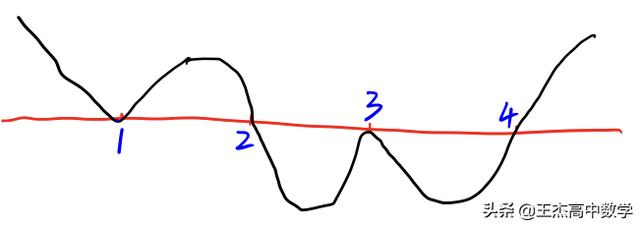
写出它的解集时需要注意“=”哟

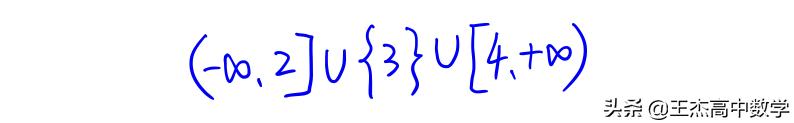
你写对了吗？

二：如果所给的高次不等式没有因式分解，而是像下面这个题似的，我们又该怎么办呢？

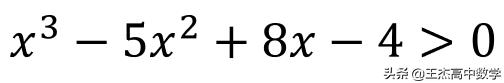
那么在这种时候我们需要冷静，需要知道如果在高中阶段出现这种三次不等式，它的解一定不会太复杂【如果太复杂的话，就不是高中阶段能解决的了】，我们只需猜根即可，一般猜1，-1，2，-2等整数值，比如本题我们将1代入，发现左边等于0，说明有一个根是1，进而得出该多项式有x-1这个因式，当我们猜出一个根，是否还需要继续猜呢？一般不需要，因为很多的时候我们无法猜出所有的根，就算猜出所有的根，也无法判断每个根具体的个数。

然后怎么办呢？利用代数式竖式除法进行因式分解

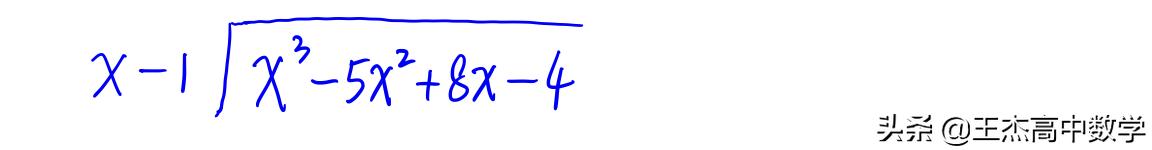
可能有些同学没见过，但小学时我们都学过整数的竖式除法，这个与它很类似

使用代数式竖式除法，先必须将多项式按指数从高到低排列，如有缺项，以0补充【后面会用例子介绍】，如下图

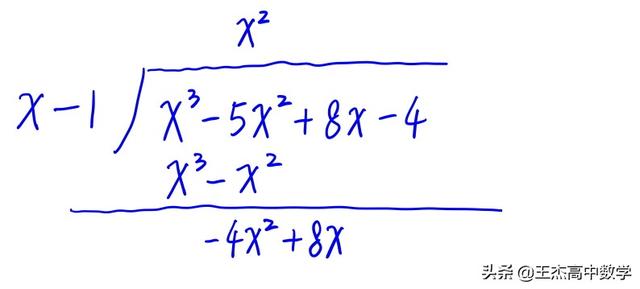
最终完整的过程如下

所以可将多项式因式分解为：

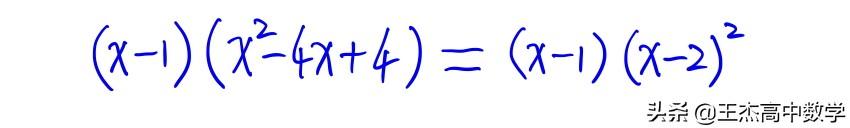
剩下的过程就和之前的可以因式分解的一样了，请同学们自己完成

我们再看一个例子

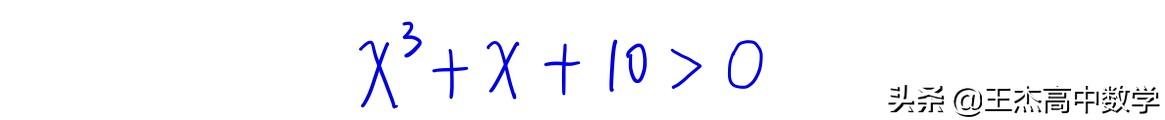
本例的多项式中没有二次项，那怎么办呢？我刚上面提过“如遇缺项，以0补充”，

先猜根，同学们应该能猜出有一个是-2吧，所以多项式能被x+2“整除”，具体如下

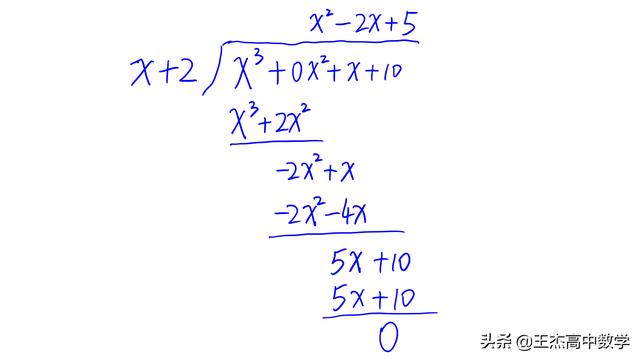
显然该多项式可以进行如下因式分解

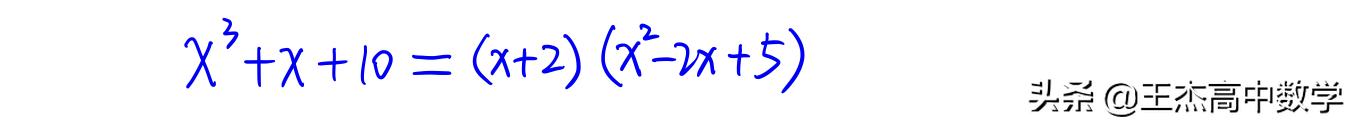
该不等式对应的根也就一目了然了，你学会了吗？同学们还可以自行举几个例子练习一下哟

三：上面两种介绍的都是整式型简单高次不等式，如果遇到分式型的呢？例如：

我们只需要将其转化为整式不等式就可以了

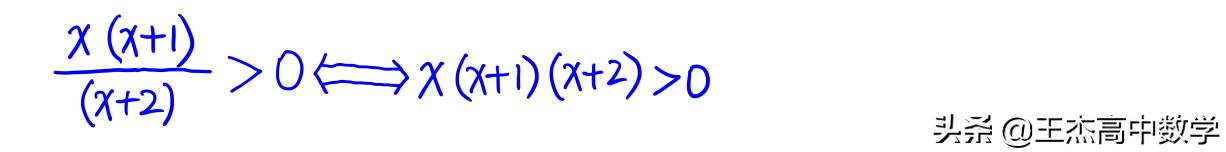
剩下的过程就和前面的一样了

只是在将分式不等式转化为整式不等式的过程中需要注意分母不为0，例如

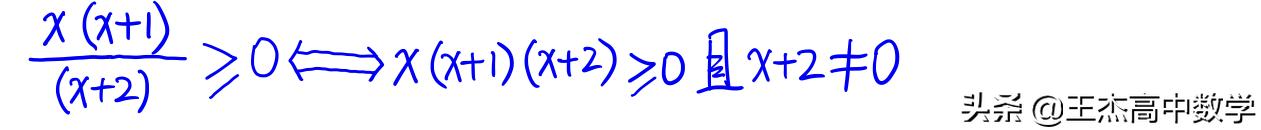
总结：

我们可以用以下“顺口溜”记忆数轴穿根法

原式化为标准型，数轴上面标出根，

奇穿偶切画曲线，上正下负解分明。

而代数式的竖式除法需要切记“从高到低，如遇缺项，以0补充”

上述文章中，本人发表了自己对高中阶段可能会涉及到的简单多项式解法的一点点浅薄的理解，如有不到之处，请各位读者朋友们不吝赐教，谢谢阅读