matlab一元线性回归分析_机器学习之整体线性回归系列总结+代码示例复现(一元线性回归/多元线性回归/岭回归LASSO/逻辑回归)...

线性回归系列汇总

一元线性回归部分笔记

关于最小二乘法的再解析

    概括地说，线性模型就是对输入的特征(样本)加权求和，再加上一个所谓的偏置项(也称截距项,或者噪声)的常数，对此加以预测

    残差平方和(RSS)：等同于SSE(误差项平方和)实际值与预测值之间差的平方之和。

    MSE(Mean Squared Error均方误差,均方差)：均方误差是RSS的期望值(或均值) MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

最小均方误差与最小二乘法的关系

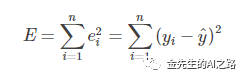
[残差平方和]

[均方误差]

    均方误差等于方差加上偏差的平方，当估计量无偏时，均方误差等于方差。所以，当满足最小二乘法条件且估计量是无偏估计量，那么求最小均方误差等价于最小二乘法。

    均方误差可以看作是加权的最小二乘法，其中的权值表示概率。所谓无偏，就是我们认为每个样本点出现的概率和真实模拟的数据中样本点出现的概率是一样的。当概率相等即无偏时，我们认为两者等价。

    最小二乘法针对的是有限的数据量的概念，而最小均方误差是针对无限数据量的一个概念。最小二乘法(LS)是最小均方误差(LMSE)在有限个观测值时的时间平均近似，或者说，当观测样本数趋于无穷大时，最小二乘估计将逼近最小均方误差估计。

    最小二乘法基于矩阵求解，最小均方误差基于概率统计求解。

    从思想的角度来理解，最小二乘法实质上是极大似然估计，是对未知模型的估计；而最小均方误差是对已知模型的参数估计，类似贝叶斯决策。

多元线性回归部分笔记

线性回归进阶模型部分笔记

逻辑回归/多元逻辑回归部分笔记

最大熵模型部分笔记

线性回归项目练习

    部分代码实例参考OREILLY 机器学习实战：基于Scikit-Learn, Keras & TensorFlow

    线性回归模型中的MSE成本函数

MSE = (X, Fw(x)) = (1/M)∑(i=1~M)(w^Txi - yi)

此处Fw(x)为假设函数

    标准方程通过线性代数方法转换得到：w^ = (X^TX)^-1 * X^T * y

此处的w^为使得成本函数最小的w值(权值)，y为目标值的向量，X为训练数据

使用标准方程来进行一元线性回归拟合

# To support both python 2 and python 3from __future__ import division, print_function, unicode_literals# Common importsimport numpy as npimport os# to make this notebook's output stable across runsnp.random.seed(42)# To plot pretty figuresimport matplotlibimport matplotlib.pyplot as plt%matplotlib inline%config InlineBackend.figure_format = 'svg'#plt.rcParams['axes.labelsize'] = 14#plt.rcParams['xtick.labelsize'] = 12#plt.rcParams['ytick.labelsize'] = 12# Where to save the figuresPROJECT_ROOT_DIR = "."CHAPTER_ID = "training_linear_models"def save_fig(fig_id, tight_layout=True):    path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")    print("Saving figure", fig_id)    if tight_layout:        plt.tight_layout()    plt.savefig(path, format='png', dpi=300)import numpy as np"""模拟的线性函数为y=3x+4+noisy"""X = 2 * np.random.rand(100, 1)  #模拟自变量X的值(100个随机值)y = 4 + 3 * X + np.random.randn(100, 1)  #模拟因变量y的值(使用自变量X计算,100个随机值)plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.axis([0, 2, 0, 15])save_fig("generated_data_plot")plt.show()

得到随机模拟点的图像为

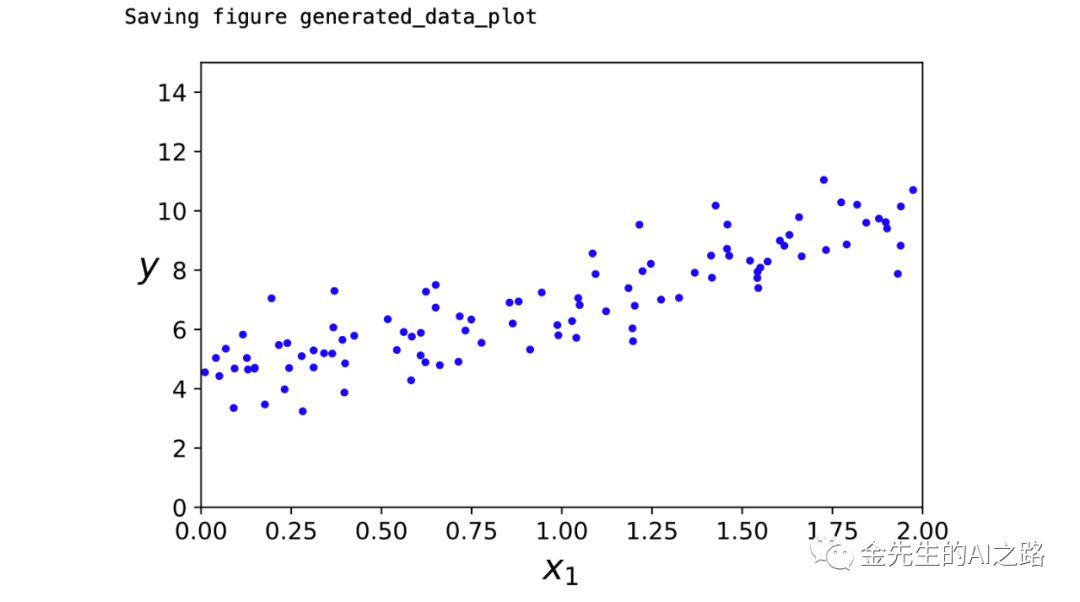
# add x0 = 1 to each instanceX_b = np.c_[np.ones((100, 1)), X]#此处X_b为自变量向量(为随机值且向量长度为100)+关于w0的为1大小为100的列向量#使用NumPy的线性代数计算模块(numpy.linalg.inv()函数来进行矩阵求逆运算)#并且使用dot()函数来计算矩阵的内积"""  此处为给为详细介绍一下：np.linalg.inv(X_b.T.dot(X_b))相当于计算(X^TX)^-1  dot(X_b.T)相当于计算(X^TX)^-1 * X^T  最终整体代码np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)计算  theta的预测值"""theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

此处X_b与theta_best的运行值为：

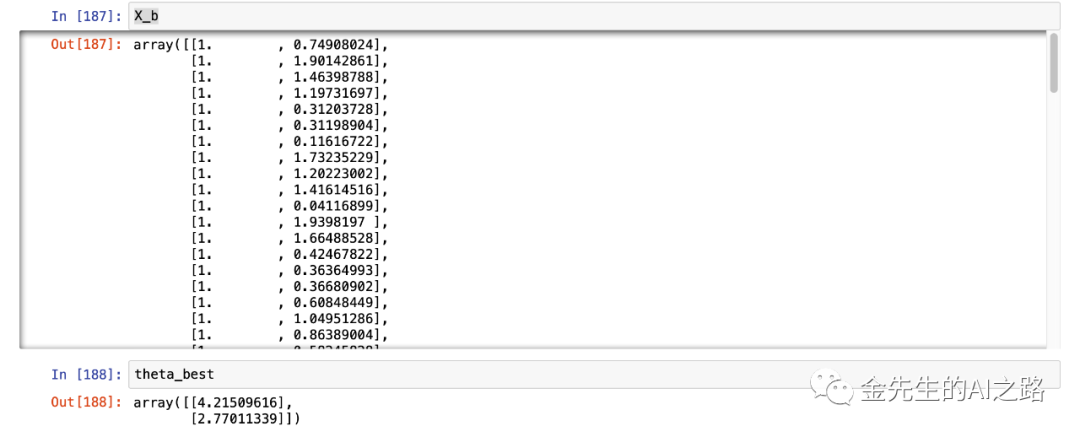
    期待的theta0=4且theta1=3，上述输出结果中theta的值因为噪声的存在大体与原来的值大体类似

#此处使用之前已经得出的theta的估计值和新的自变量X来预测新的y值#自变量前面添加w0=1进而得到最后的X_new_b#X_new_b为一个2*2矩阵X_new = np.array([[0], [2]])X_new_b = np.c_[np.ones((2, 1)), X_new]  # add x0 = 1 to each instancey_predict = X_new_b.dot(theta_best)print(y_predict)plt.plot(X_new, y_predict, "r-", linewidth=2, label="Predictions")plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.legend(loc="upper left", fontsize=14)plt.axis([0, 2, 0, 15])save_fig("linear_model_predictions")plt.savefig('/Users/jinzewei/Desktop/普通线性回归.png') # save the figure to fileplt.show()plt.close() # close the figure

值中得出的预测曲线为：

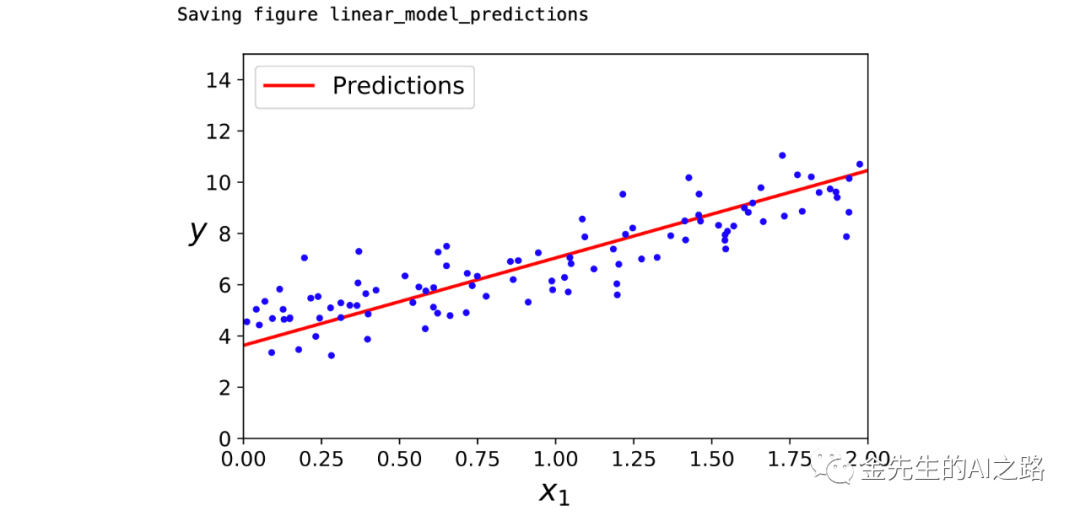
之后我们再次使用Sklearn模块中的LinearRegression函数来进行框架的模块跨预测

from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()lin_reg.fit(X, y)print(lin_reg.intercept_, lin_reg.coef_)#此处的lin_reg.intercept_为w0，lin_reg.coef_为w1#高次项情形同理，intercept_为w0，coef_表示w1~wnlin_reg.predict(X_new)

最终得出的预测值为：

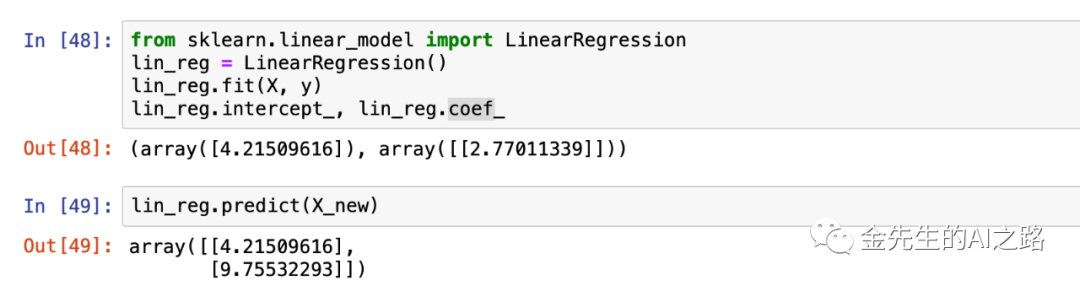
绘图表示：

plt.plot(X_new, lin_reg.predict(X_new), "g-", linewidth=2, label="Predictions By Sklearn Linear Model")plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.legend(loc="upper left", fontsize=14)plt.axis([0, 2, 0, 15])save_fig("linear_model_predictions By Sklearn's LinearRegression Model")plt.savefig('/Users/jinzewei/Desktop/Sklearn线性回归.png') # save the figure to fileplt.show()

‍

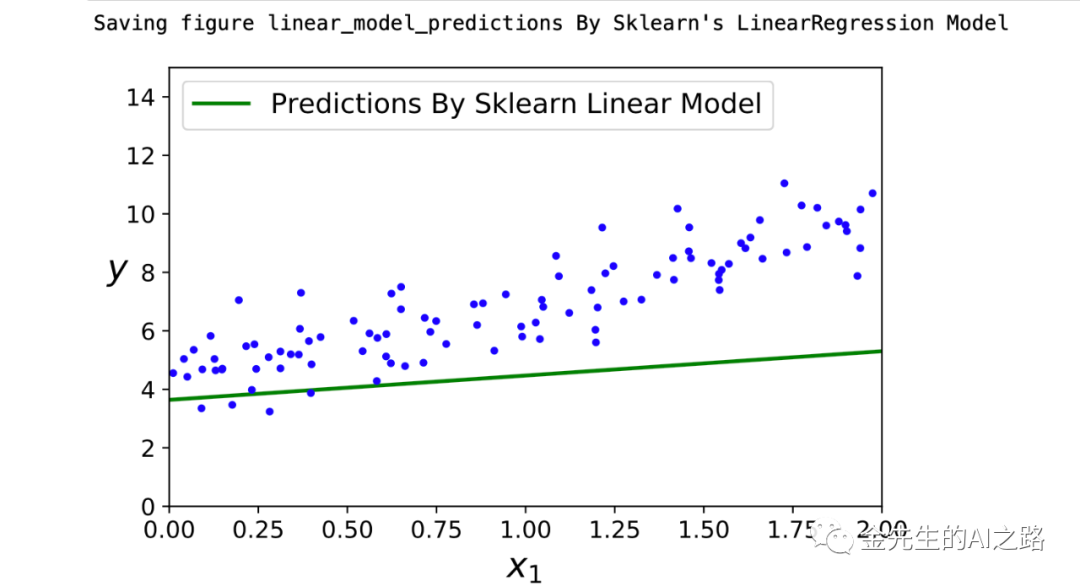
结合上面一元线性回归的两幅图得出，有时候Sklearn模块的训练精度并不高，因为图一中的直线拟合更接近原石距样本的散布程度

梯度下降部分实例

    关于梯度下降法远离部分不做过多赘述

    具体参考之前公众号文章：最优化导论(Machine Learning)梯度方法

    *Hint：

        令函数的x(0)作为初始搜索点，并沿着负梯度方向构造一个新点x(0)-å▽f(x(0))可由泰勒定理得出：

f(x(0) - å▽f(x(0))) = f(x(0)) - å||▽f(x(0))||^2+O(å)

所以，如果▽f(x(0)) != 0，那么当å > 0足够小时，有

f(x(0) - å▽f(x(0))) < f(x(0))

成立 即，从搜索目标函数极小点的角度来看，x(0) - å▽f(x(0))相对于x(0)有所下降的改善和趋势

        最速下降法(梯度下降法)根据上述理念，设定一个搜索点x(k)，由此点出发，根据向量-åk▽f(x(k))指定的方向和幅度移动，构造一个新的点x(k+1)，其中åk为一个正实数，称之为步长，由此得到其迭代公式：

x(k+1) = x(k) -åk▽f(x(k))这称之为梯度下降法的迭代公式，在搜索过程中，梯度不断变化，当接近极小点时，梯度趋近为0 {▽f(x) = 0 相当于一阶导数斜率为0}    最速下降法是梯度下降法的具现，在每次迭代中选择合适的步长åk，使得目标函数值能够得到最大程度地减小 åk实际上为函数øk(å) = f(x(k) - å▽f(x(k)))的极小点 即，åk = arg min(å>=0) f(x(k) - å▽f(x(k)))    *最速下降法在每步迭代中，从迭代点x(k)出发，沿着负梯度方向 -▽f(x(k))开展一维搜索，直到找到步长的最优值，确定新的迭代点x(k+1)，最速下降法的相邻搜索方向是正交的

eta = 0.1  #学习率设置为0.1n_iterations = 1000  #迭代1000次m = 100  #解释变量(自变量)个数为100个theta = np.random.randn(2,1)for iteration in range(n_iterations):    #此处对应的原梯度计算公式为：∂MSE(θ)/∂θj = 2/m(θ^T*X(i) - y(i)xj(i))    gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)    #此处为梯度下降的迭代步骤θ(n+1) = θ - η▽MSE(▽)    theta = theta - eta * gradientstheta_path_bgd = []#绘制出梯度下降的图像，依照学习率大小各自区分绘制def plot_gradient_descent(theta, eta, theta_path=None):    m = len(X_b)    plt.plot(X, y, "b.")    n_iterations = 1000  #迭代1000次    for iteration in range(n_iterations):        if iteration < 10:            y_predict = X_new_b.dot(theta)  #预测值y，依照回归模型中预测的theta值来乘以自变量x来对其进行预测            style = "b-" if iteration > 0 else "r--"            plt.plot(X_new, y_predict, style)        #此处为梯度值，原梯度计算公式为：∂MSE(θ)/∂θj = 2/m(θ^T*X(i) - y(i)xj(i))        gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)        #此处为梯度下降的迭代步骤θ(n+1) = θ - η▽MSE(▽)        theta = theta - eta * gradients        if theta_path is not None:            theta_path.append(theta)    plt.xlabel("$x_1$", fontsize=18)    plt.axis([0, 2, 0, 15])    plt.title(r"$\eta = {}$".format(eta), fontsize=16)np.random.seed(42)theta = np.random.randn(2,1)  # random initializationplt.figure(figsize=(20,10))plt.subplot(231); plot_gradient_descent(theta, eta=0.02)plt.ylabel("$y$", rotation=0, fontsize=18)plt.subplot(232); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)plt.subplot(233); plot_gradient_descent(theta, eta=0.5)plt.subplot(234); plot_gradient_descent(theta, eta=0.75)plt.ylabel("$y$", rotation=0, fontsize=18)plt.subplot(235); plot_gradient_descent(theta, eta=1)plt.subplot(236); plot_gradient_descent(theta, eta=1.025)save_fig("gradient_descent_plot")plt.savefig('/Users/jinzewei/Desktop/梯度下降.png') # save the figure to fileplt.show()plt.close() # close the figure

最终输出的依据梯度各自为η=0.02，η=0.1，η=0.5，η=0.75，η=1，η=1.025的学习率生成的梯度下降图像为：

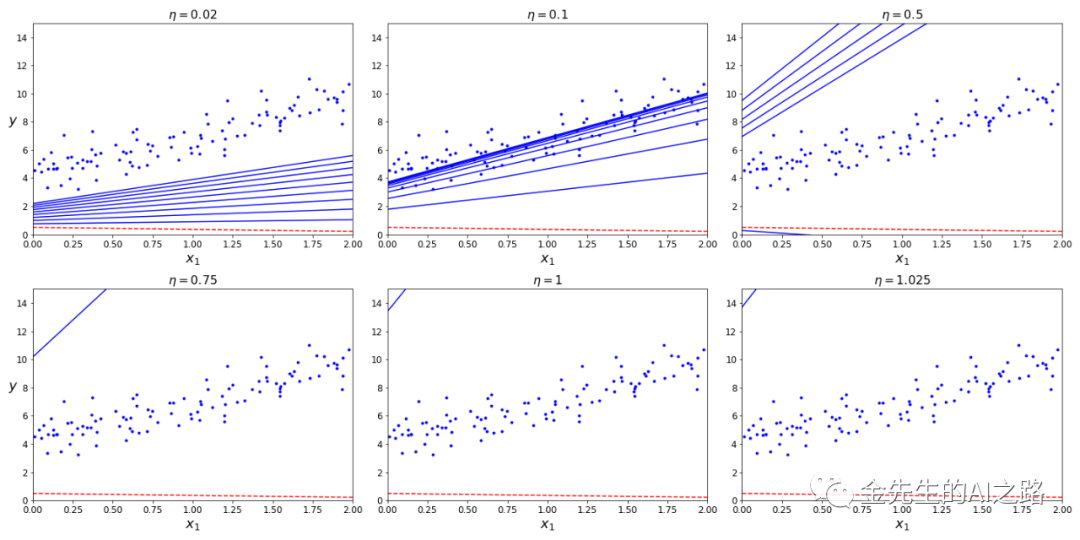
随机梯度下降

theta_path_sgd = []m = len(X_b)  #m为X_b即自变量数据集的大小 m=100np.random.seed(42)n_epochs = 50t0, t1 = 5, 50  # learning schedule hyperparameters学习超参数def learning_schedule(t):  #计算新的学习率函数    return t0 / (t + t1)theta = np.random.randn(2,1)  # random initialization"""   进行m=100个回合迭代，每回合称为一个轮次   虽然在批量梯度下降中整个训练集合中进行1000次迭代   但是此处代码最后仅仅在训练集中遍历25次，差不多能达到最优答案"""for epoch in range(n_epochs):    for i in range(m):        if epoch == 0 and i #迭代训练25代            y_predict = X_new_b.dot(theta)      #X*theta计算            style = "b--" if i > 0 else "r--"            plt.plot(X_new, y_predict, style)        random_index = np.random.randint(m)    #返回一个随机整型数，范围从0到m        xi = X_b[random_index:random_index+1]  #截取保存自变量Xi(i=random_index)的随机抽取的自变量数据        yi = y[random_index:random_index+1]    #截取保存因变量yi(i=random_index)的随机抽取的因变量数据        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)  #计算梯度值        eta = learning_schedule(epoch * m + i)  #5/(50 + (epoch*m+i))新的学习率随着m和i增大而降低        theta = theta - eta * gradients    #根据梯度下降递推公式计算并刷新新的theta值        theta_path_sgd.append(theta)    #在对应的数组中记录每一步计算得到的theta值plt.plot(X, y, "r.")                                 # not shownplt.xlabel("$x_1$", fontsize=18)                     # not shownplt.ylabel("$y$", rotation=0, fontsize=18)           # not shownplt.axis([0, 2, 0, 15])                              # not shownsave_fig("sgd_plot")                                 # not shown#plt.savefig('/Users/jinzewei/Desktop/25次梯度下降集合图.png') # save the figure to fileplt.show()plt.close() # close the figure

最终随机梯度下降得到的图像为：

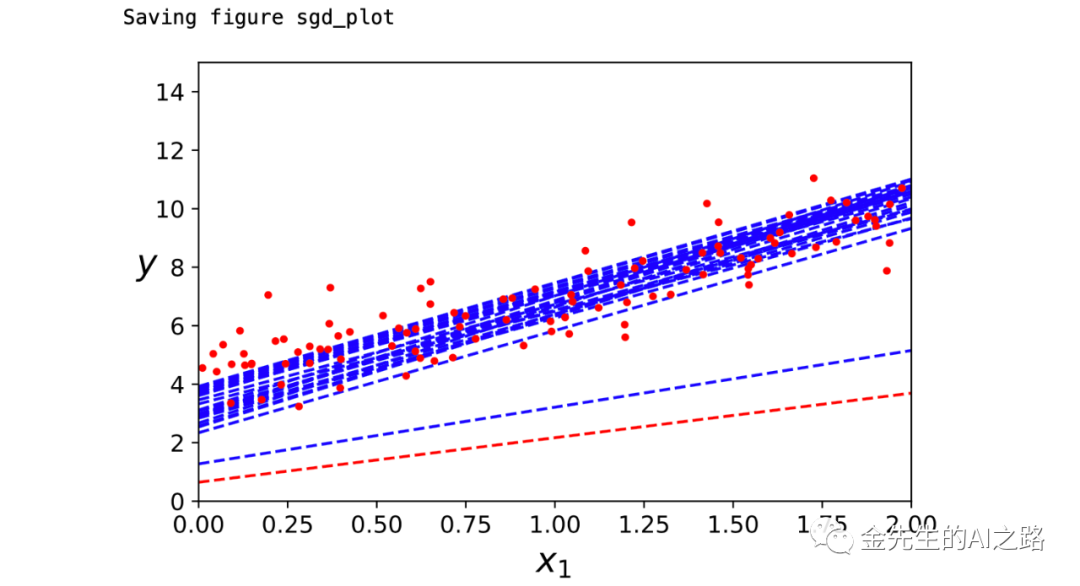
    随机梯度下降的优点是，在刚开始的既不中可以用大学习率逃离局部最优解(局部最小解)，且由于随机性，随机梯度下降的路径不是规则的一直向下，而是不断上上下下，但从宏观的整体来分析，最终还是趋近于收敛至最小值的。但是即便随机梯度下降达到了最小值(最优解)，依旧会接着持续反弹，永远不停止。即该算法停下来时所求的参数值肯定是足够好的，但不是最优解，对此解决这个永远定位不出最小值的缺憾，所作的解决方法时逐步降低学习率

使用Sklearn模块中的SGDRegression类进行随机梯度下降

    使用随机梯度下降方法时，训练实例必须独立且保证均匀分布，以用来确保平均将参数拉向全局最优值。确保该独立且均匀的简单方法是在训练过程中对实例进行混洗(随机选择每个实例，或者在每个轮次开始时随机混洗训练集合)如果不对实例进行混洗，SGDRegression类将针对每一个标签进行优化，并且不会接近全局最小值，该类默认优化平方误差成本函数。

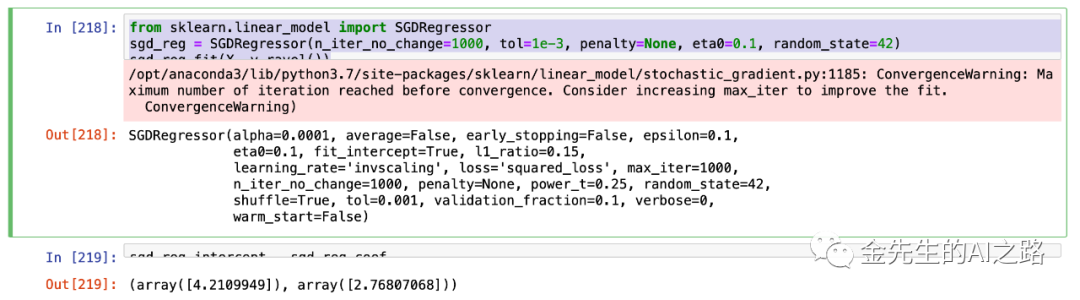
from sklearn.linear_model import SGDRegressorsgd_reg = SGDRegressor(n_iter_no_change=1000,                        tol=1e-3, penalty=None,                       eta0=0.1, random_state=42)sgd_reg.fit(X, y.ravel())sgd_reg.intercept_, sgd_reg.coef_

    上述代码运行最多1000轮次，直到一个轮次期间损失下降到小于0.001为止，并使用默认的学习调度，以eta=0.1的学习率开始，并且不使用任何正则化penalty=0

    最终输出非常接近标准方程的解

小批量梯度下降

    简单总结：小批量梯度下降在每一步中，并不是根据完整的训练集(类似批量梯度下降)，或者是仅仅基于一个实例(类似随机梯度下降)来计算梯度。其在称为小型批量随机实例集合上计算梯度。与之前的随机梯度下降相比，该算法在参数空间上的进程更加稳定，在相当大的小批次中，小批量梯度下降最终将比随机梯度下降更能接近最小值，但也存在无法摆脱局部最小值的情形

下列代码显示并绘制出训练期间参数空间中3种梯度下降法所采用的路径

theta_path_mgd = []n_iterations = 50      #迭代次数minibatch_size = 20    #最小批量梯度下降的间隔大小np.random.seed(42)theta = np.random.randn(2,1)  # random initializationt0, t1 = 10, 1000def learning_schedule(t):    #计算新的学习率    return t0 / (t + t1)t = 0for epoch in range(n_iterations):    shuffled_indices = np.random.permutation(m)    #使用np.random.permutation()方法打乱原来数据中的元素，但并不改变数据维度    X_b_shuffled = X_b[shuffled_indices]    #此处相当于打乱原自变量数据数组的index，并提取打乱后的自变量数据    y_shuffled = y[shuffled_indices]    #与之对应此处相当于打乱对应的因变量数据index，且顺序同自变量X，并提取打乱后的因变量数据y    for i in range(0, m, minibatch_size):    #m=100 len(X_b)        t += 1    #每轮循环中t增加一个大小        xi = X_b_shuffled[i:i+minibatch_size]        yi = y_shuffled[i:i+minibatch_size]        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)        eta = learning_schedule(t)        theta = theta - eta * gradients    #根据梯度下降递推公式计算并刷新新的theta值        theta_path_mgd.append(theta)    #在对应的数组中记录每一步计算得到的theta值print(theta)#使用np.array()方法转化数组为numpy模块中的数组形式theta_path_bgd = np.array(theta_path_bgd)  #批量梯度下降theta_path_sgd = np.array(theta_path_sgd)  #随机梯度下降theta_path_mgd = np.array(theta_path_mgd)  #小批量梯度下降plt.figure(figsize=(7,4))plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic随机梯度")plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch小批量")plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch批量")plt.legend(loc="upper left", fontsize=16)plt.xlabel(r"$\theta_0$", fontsize=20)plt.ylabel(r"$\theta_1$   ", fontsize=20, rotation=0)plt.axis([2.5, 4.5, 2.3, 3.9])save_fig("gradient_descent_paths_plot")plt.show()

下图为参数空间中三种梯度下降方法的下降路径：‍

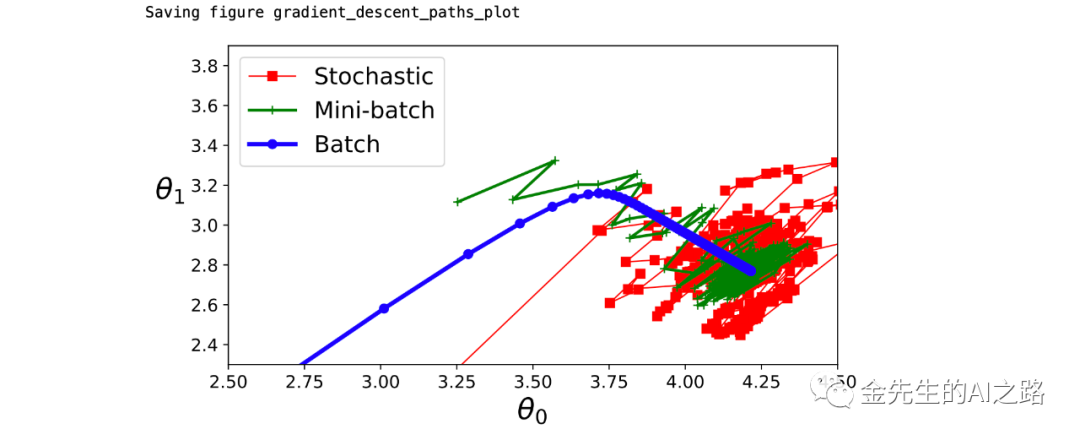
分析红绿蓝三条下降路径(红:随机梯度/绿:小批量梯度/蓝:批量梯度)，可以发现三种梯度方法最终都接近最小值，批量梯度下降的路径实际上是在最小值处停止，但是随机梯度下降和小批量梯度下降都在之后继续运动，而且也可以清晰看出批量梯度下降耗时最多，随机梯度下降的无序性最强(无头苍蝇一样的随意摆动)，小批量梯度下降位于两者之间(因其定义了小批量的间隔大小并初始打乱了变量数据的顺序)

多项式回归

    基于简单的二次方程(y=ax^2 + bx + c + noisy)生成非线性数据

# Polynomial regressionimport numpy as npimport numpy.random as rndnp.random.seed(42)m = 100X = 6 * np.random.rand(m, 1) - 3y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)plt.plot(X, y, "b.")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.axis([-3, 3, 0, 10])save_fig("quadratic_data_plot")plt.show()

生成的简单二次方程+噪声的样本点分布图像为：

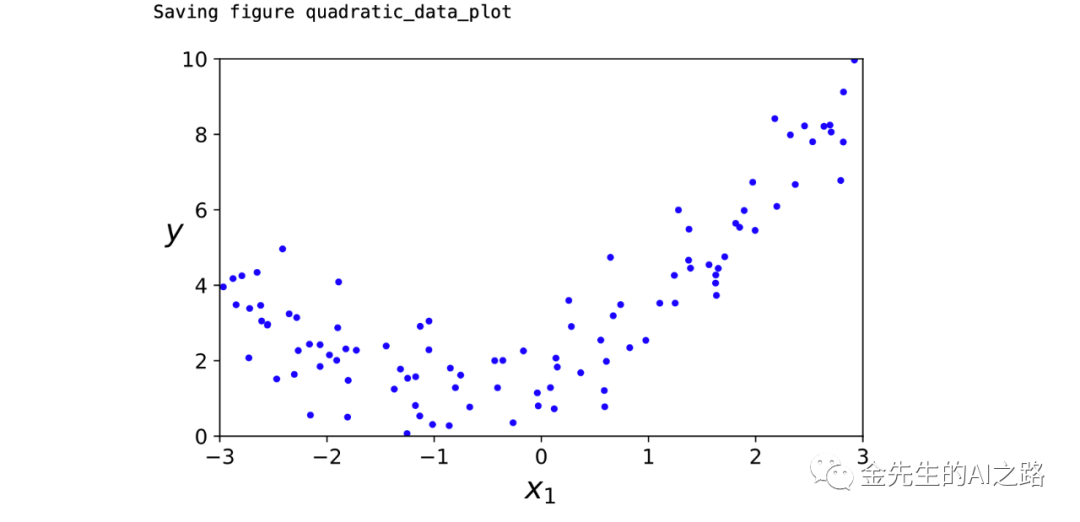
    之后采用Sklearn模块中的PolynomialFeatures类来进行训练数据的转换，将训练集合中的每个特征的平方(二次多项式)添加为新特征(即转化为一个特征)

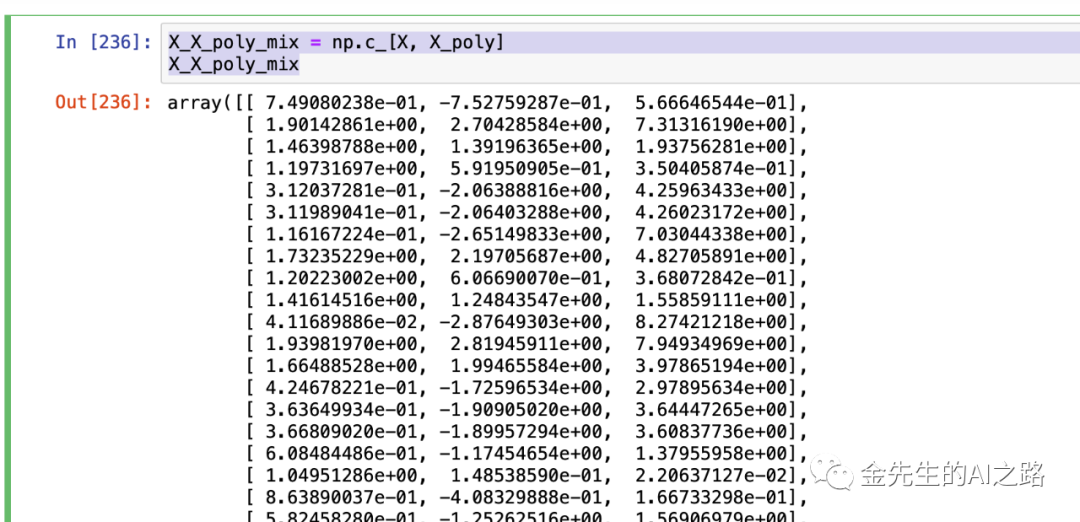
#Features Transform特征转换from sklearn.preprocessing import PolynomialFeaturespoly_features = PolynomialFeatures(degree=2, include_bias=False)X_poly = poly_features.fit_transform(X)X_X_poly_mix = np.c_[X, X_poly]X_X_poly_mix

最终可以看见组合后的特征转换值为：

X_poly现在包涵X的原始特征以及该特征的平方

之后再将LinearRegression模型拟合到代扩展后的训练数据集中

lin_reg = LinearRegression()lin_reg.fit(X_poly, y)print(lin_reg.intercept_, lin_reg.coef_)X_new=np.linspace(-3, 3, 100).reshape(100, 1)X_new_poly = poly_features.transform(X_new)y_new = lin_reg.predict(X_new_poly)plt.plot(X, y, "b.")plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.legend(loc="upper left", fontsize=14)plt.axis([-3, 3, 0, 10])save_fig("quadratic_predictions_plot")plt.show()

Hint：依据二次方程(y=0.5x^2+x+2+noisy) 

          intercept_为w0(此处表示噪音)

          coef_表示(w1~wn)    w1=coef_[0]第一个位置数据(原式一次项系数)                w2=coef[1]第二个未知的数据(原式二次项系数)

最后绘图得到拟合的多项式回归曲线为：

⚠️Warning：多项式存在多个特征时，多项式回归能够找到特征之间的关系，且普通线性回归模型无法做到。PolynomialFeatures还可以将特征的所有组合添加到给定的多项式阶数。PolynomialFeatures(degree=d)该类可以将一个包含n个特征的数组转换为包含(n+d)!/d!n!个特征的数组，故此处应注意特征组合数组的维数爆炸情形！

学习曲线

    高阶多项式回归与普通线性回归相比拟合数据会更好。此处给出300阶多项式模型应用于先前的训练数据集合。

from sklearn.preprocessing import StandardScalerfrom sklearn.pipeline import Pipeline#定义线段样式g,b,r  线段宽度  多项式阶数for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):    polybig_features = PolynomialFeatures(degree=degree, include_bias=False)    #StandardScaler()标准化数据通过减去均值然后除以方差(或标准差)    #该数据标准化方法经过处理后数据符合标准正态分布    #即均值为0，标准差为1，转化函数为：x =(x - ?)/?    std_scaler = StandardScaler()    lin_reg = LinearRegression()    polynomial_regression = Pipeline([            ("poly_features", polybig_features),            ("std_scaler", std_scaler),            ("lin_reg", lin_reg),        ])    polynomial_regression.fit(X, y)    y_newbig = polynomial_regression.predict(X_new)    plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)plt.plot(X, y, "b.", linewidth=3)plt.legend(loc="upper left")plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", rotation=0, fontsize=18)plt.axis([-3, 3, 0, 10])save_fig("high_degree_polynomials_plot")plt.show()

最终得到的三种回归模型的拟合图像为：

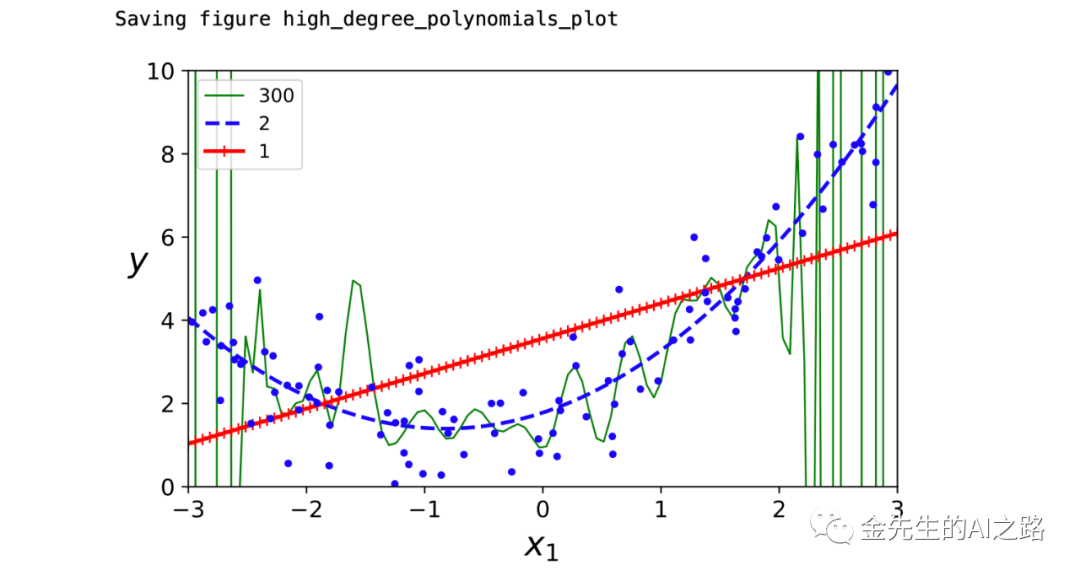
    由图像可以轻易看出，高阶多项式回归模型存在严重的过拟合情况训练数据，而简单的一元线性回归模型则存在欠拟合，最具有泛化行且最能体现训练数据的拟合情况是二次模型。可以依据交叉验证来评估模型的泛化性能(模型在训练数据表现良好->交叉验证指标泛化性能较差->存在过拟合)OR(模型在训练数据表现较差->交叉验证指标泛化性能较差->存在欠拟合)

通过绘制学习曲线来鉴别模型性能：该曲线绘制的是模型在训练集合和测试集合上关于训练集大小(或训练迭代次数)的性能函数，要生成该曲线，只需在不同大小的子训练集合上多次训练即可

from sklearn.metrics import mean_squared_error  #MSE均方误差from sklearn.model_selection import train_test_split  #训练/测试集合划分def plot_learning_curves(model, X, y):    #X_train:训练集合自变量 X_val:测试集合自变量    #y_train:训练集合因变量 y_val:测试集合因变量    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)    train_errors, val_errors = [], []  #定义误差(训练集合/测试集合)    for m in range(1, len(X_train)):  #遍历训练集合大小        model.fit(X_train[:m], y_train[:m])        y_train_predict = model.predict(X_train[:m])        y_val_predict = model.predict(X_val)        train_errors.append(mean_squared_error(y_train_predict, y_train[:m]))        val_errors.append(mean_squared_error(y_val_predict, y_val))    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")    plt.legend(loc="upper right", fontsize=14)    plt.xlabel("Training set size", fontsize=14)    plt.ylabel("RMSE", fontsize=14)lin_reg = LinearRegression()plot_learning_curves(lin_reg, X, y)plt.axis([0, 80, 0, 3])save_fig("underfitting_learning_curves_plot")plt.show()

生成的学习曲线为下图：

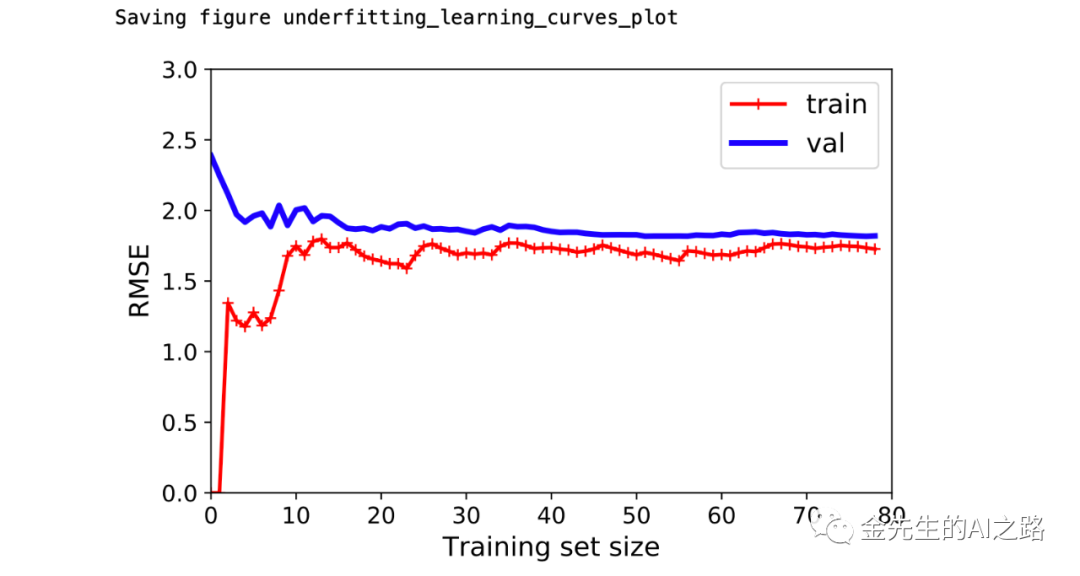
    依据上图学习曲线有如下分析：当训练集合只有一个或两个实例时，模型能够很好的拟合数据，这即为训练集曲线从0开始的原因，之后随着实例不断增加到训练集合中模型就不能非常完美的拟合训练数据(因为数据中存在噪声或者根部非线性数据)，因此，训练数据的误差会不断上升(红色曲线上升)，直到最终达到一个平稳状态(此时再添加或减少训练集合的新实例并不会显著影响平均误差更好或者更坏) 在测试集合中模型的性能，初始时因为训练数据很少所以导致模型不可能正确泛化，也即验证误差最初很大的原因。之后随着更多的训练实例添加进来，模型逐步优化学习，验证错误逐渐降低。但是直线并不能很好的对数据进行建模，故测试集的误差最终也稳定于一个范围，两条曲线渐进贴合。

逻辑回归示例

    参照先前的纸质扫描件笔记Logistic Regression该种类的回归算法同理可以被用来进行分类运算，此处对具体的数学推导不做过多赘述，详情参考之前笔记

    此处给出与逻辑回归密切相关的Logit函数图像

# Logistic regressiont = np.linspace(-10, 10, 100)sig = 1 / (1 + np.exp(-t))plt.figure(figsize=(9, 3))plt.plot([-10, 10], [0, 0], "k-")plt.plot([-10, 10], [0.5, 0.5], "k:")plt.plot([-10, 10], [1, 1], "k:")plt.plot([0, 0], [-1.1, 1.1], "k-")plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")plt.xlabel("t")plt.legend(loc="upper left", fontsize=20)plt.axis([-10, 10, -0.1, 1.1])save_fig("logistic_function_plot")plt.show()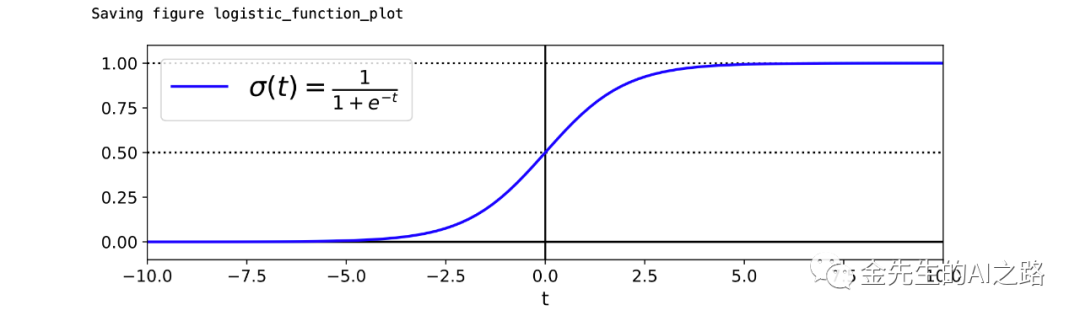

关于被玩了一百遍的维吉尼亚鸢尾花数据给出基于Logit函数生成的2分类模型

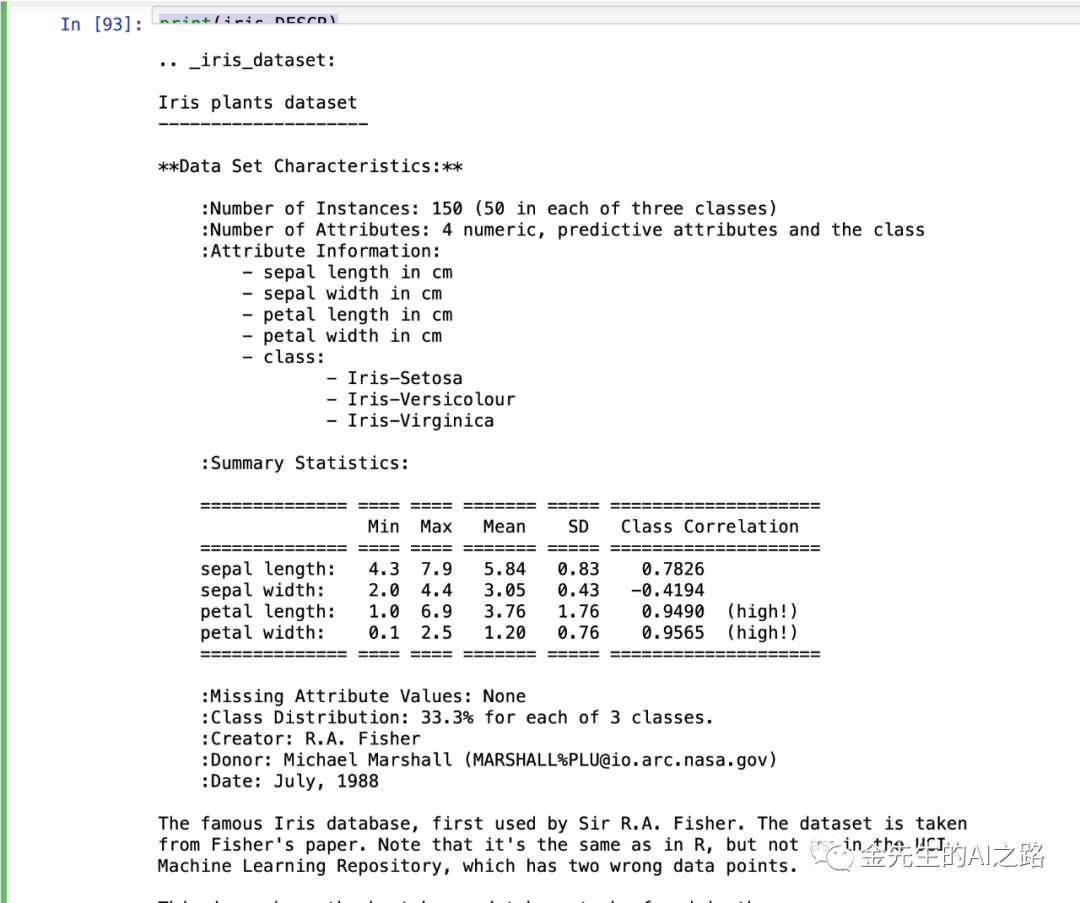
from sklearn import datasetsiris = datasets.load_iris()  #加载鸢尾花数据list(iris.keys())print(iris.DESCR)  #鸢尾花数据文档说明X = iris["data"][:, 3:]  # petal width# 1 if Iris-Virginica, else 0y = (iris["target"] == 2).astype(np.int)X_new = np.linspace(0, 3, 1000).reshape(-1, 1)y_proba = log_reg.predict_proba(X_new)X_new = np.linspace(0, 3, 1000).reshape(-1, 1)y_proba = log_reg.predict_proba(X_new)decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]plt.figure(figsize=(8, 3))plt.plot(X[y==0], y[y==0], "bs")plt.plot(X[y==1], y[y==1], "g^")plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris-Virginica")plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris-Virginica")plt.text(decision_boundary+0.02, 0.15, "Decision  boundary", fontsize=14, color="k", ha="center")plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')plt.xlabel("Petal width (cm)", fontsize=14)plt.ylabel("Probability", fontsize=14)plt.legend(loc="center left", fontsize=14)plt.axis([0, 3, -0.02, 1.02])save_fig("logistic_regression_plot")plt.show()print(decision_boundary)    #决策边界：array([1.61561562])print(log_reg.predict([[1.7], [1.5]]))  #预测值：array([1, 0])

鸢尾花数据文档说明如下：

逻辑回归分类的鸢尾花决策范围定义图像：

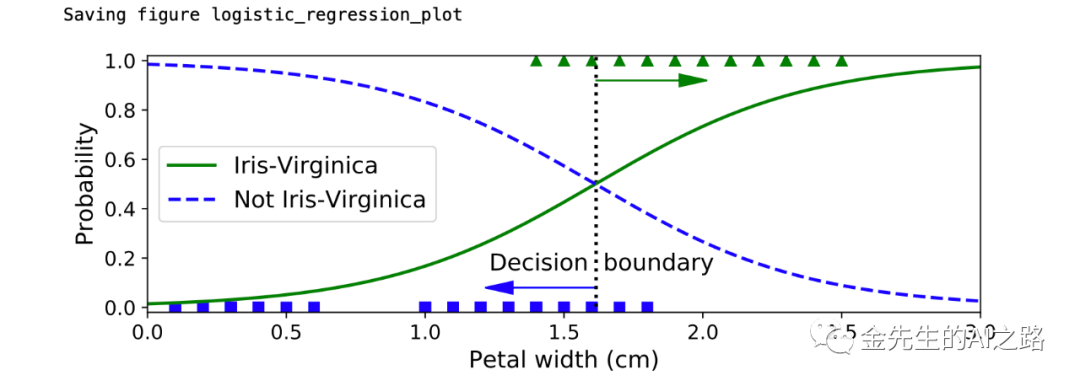
鸢尾花二分类二维分界

å =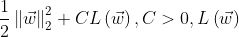 

from sklearn.linear_model import LogisticRegressionX = iris["data"][:, (2, 3)]  #读取花瓣长度，花瓣宽度数据y = (iris["target"] == 2).astype(np.int)#C规定了惩罚系数的倒数#如果为'l2'范数，则优化目标函数å为极大似然函数log_reg = LogisticRegression(C=10**10, random_state=42)log_reg.fit(X, y)x0, x1 = np.meshgrid(        #给出范围为2.9～7的500个等差数据，用来模拟测试集合的花瓣长度        np.linspace(2.9, 7, 500).reshape(-1, 1),        #给出范围为0.8～2.7的200个等差数据，用来模拟测试集合的花瓣宽度        np.linspace(0.8, 2.7, 200).reshape(-1, 1),#生成大小为100000的测试数据进行分类预测X_new = np.c_[x0.ravel(), x1.ravel()]#predict_proba返回的是一个 n 行 k 列的数组#第 i 行 第 j 列上的数值是模型预测#第 i 个预测样本为某个标签的概率，并且每一行的概率和为1。y_proba = log_reg.predict_proba(X_new)  #进行测试数据集预测plt.figure(figsize=(10, 4))plt.plot(X[y==0, 0], X[y==0, 1], "bs")plt.plot(X[y==1, 0], X[y==1, 1], "g^")zz = y_proba[:, 1].reshape(x0.shape)contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)left_right = np.array([2.9, 7])boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]plt.clabel(contour, inline=1, fontsize=12)plt.plot(left_right, boundary, "k--", linewidth=3)plt.text(3.5, 1.5, "Not Iris-Virginica", fontsize=14, color="b", ha="center")plt.text(6.5, 2.3, "Iris-Virginica", fontsize=14, color="g", ha="center")plt.xlabel("Petal length", fontsize=14)plt.ylabel("Petal width", fontsize=14)plt.axis([2.9, 7, 0.8, 2.7])save_fig("logistic_regression_contour_plot")plt.show()

最终依据花瓣长度-花瓣宽度判别是否为鸢尾花得到的二分类图像为：

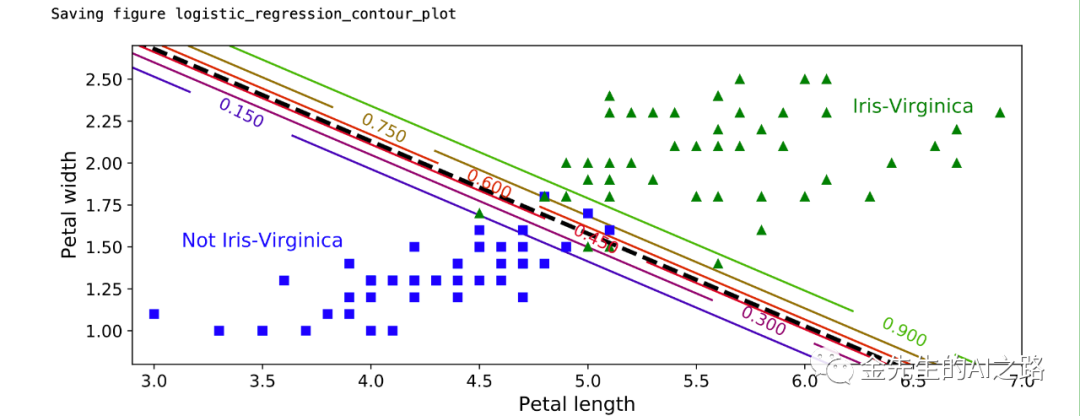
多元逻辑回归：SoftMax交叉熵回归模型

X = iris["data"][:, (2, 3)]  # petal length, petal widthy = iris["target"]#multi_多元逻辑回归定义softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)softmax_reg.fit(X, y)x0, x1 = np.meshgrid(        #给出范围为0～8的500个等差数据，用来模拟测试集合的花瓣长度        np.linspace(0, 8, 500).reshape(-1, 1),        #给出范围为0～3.5的200个等差数据，用来模拟测试集合的花瓣宽度        np.linspace(0, 3.5, 200).reshape(-1, 1),    )X_new = np.c_[x0.ravel(), x1.ravel()]  #生成100000个测试数据进行分类预测#测试数据样本点为0，1，2三类的概率y_proba = softmax_reg.predict_proba(X_new)#测试数据样本点为0，1，2类的具体给出答案y_predict = softmax_reg.predict(X_new)zz1 = y_proba[:, 1].reshape(x0.shape)zz = y_predict.reshape(x0.shape)plt.figure(figsize=(10, 4))#第2类：维吉尼亚鸢尾花种类 第1类：变色鸢尾种类 第0类：山鸢尾种类plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris-Virginica")plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris-Versicolor")plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris-Setosa")from matplotlib.colors import ListedColormapcustom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])plt.contourf(x0, x1, zz, cmap=custom_cmap, linewidth=5)contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)plt.clabel(contour, inline=1, fontsize=12)plt.xlabel("Petal length", fontsize=14)plt.ylabel("Petal width", fontsize=14)plt.legend(loc="center left", fontsize=14)plt.axis([0, 7, 0, 3.5])save_fig("softmax_regression_contour_plot")plt.show()

最终得出的三分类模型(维吉尼亚鸢尾/变色鸢尾/山鸢尾)的分类图像为：

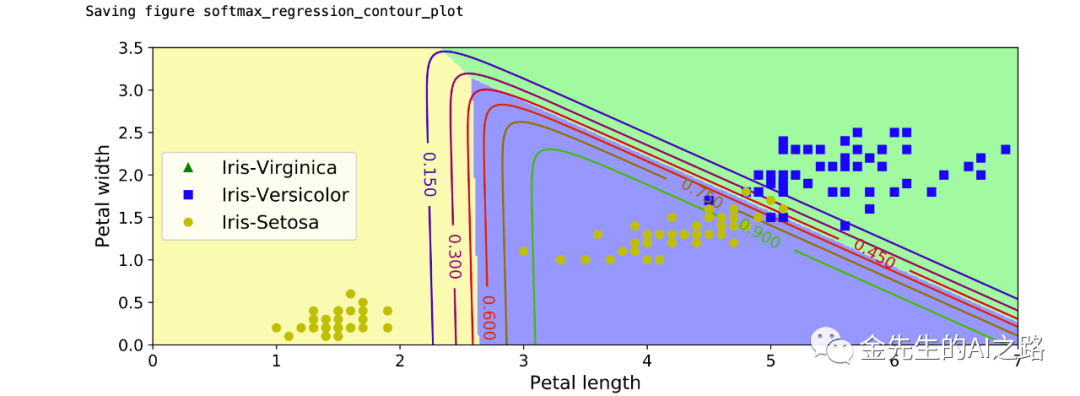
岭回归与LASSO

%matplotlib inlineimport matplotlib.pyplot as pltimport numpy as npt1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5# ignoring bias termt1s = np.linspace(t1a, t1b, 500)t2s = np.linspace(t2a, t2b, 500)t1, t2 = np.meshgrid(t1s, t2s)T = np.c_[t1.ravel(), t2.ravel()]Xr = np.array([[-1, 1], [-0.3, -1], [1, 0.1]])yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)t_min_idx = np.unravel_index(np.argmin(J), J.shape)t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]t_init = np.array([[0.25], [-1]])def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.1, n_iterations = 50):    path = [theta]    for iteration in range(n_iterations):        gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + 2 * l2 * theta        theta = theta - eta * gradients        path.append(theta)    return np.array(path)plt.figure(figsize=(12, 8))for i, N, l1, l2, title in ((0, N1, 0.5, 0, "Lasso"), (1, N2, 0,  0.1, "Ridge")):    JR = J + l1 * N1 + l2 * N2**2        tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)    t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]    levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)    levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)    levelsN=np.linspace(0, np.max(N), 10)        path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)    path_JR = bgd_path(t_init, Xr, yr, l1, l2)    path_N = bgd_path(t_init, Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)    plt.subplot(221 + i * 2)    plt.grid(True)    plt.axhline(y=0, color='k')    plt.axvline(x=0, color='k')    plt.contourf(t1, t2, J, levels=levelsJ, alpha=0.9)    plt.contour(t1, t2, N, levels=levelsN)    plt.plot(path_J[:, 0], path_J[:, 1], "w-o")    plt.plot(path_N[:, 0], path_N[:, 1], "y-^")    plt.plot(t1_min, t2_min, "rs")    plt.title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)    plt.axis([t1a, t1b, t2a, t2b])    plt.subplot(222 + i * 2)    plt.grid(True)    plt.axhline(y=0, color='k')    plt.axvline(x=0, color='k')    plt.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)    plt.plot(path_JR[:, 0], path_JR[:, 1], "w-o")    plt.plot(t1r_min, t2r_min, "rs")    plt.title(title, fontsize=16)    plt.axis([t1a, t1b, t2a, t2b])for subplot in (221, 223):    plt.subplot(subplot)    plt.ylabel(r"$\theta_2$", fontsize=20, rotation=0)for subplot in (223, 224):    plt.subplot(subplot)    plt.xlabel(r"$\theta_1$", fontsize=20)save_fig("lasso_vs_ridge_plot")plt.show()

最终生成的LASSO回归图像为：

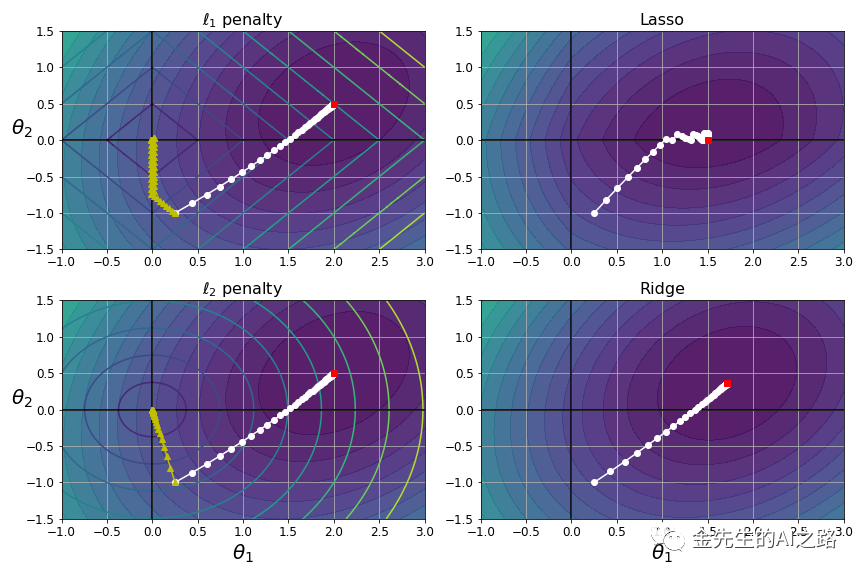
整理不易，且学且珍惜

数学是一种精神，一种理性的精神。正是这种精神，激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度，亦正是这种精神，试图决定性地影响人类的物质、道德和社会生活；试图回答有关人类自身存在提出的问题；努力去理解和控制自然；尽力去探求和确立已经获得知识的最深刻的和最完美的内涵。——克莱因《西方文化中的数学》

参考文献：OREILLY 机器学习实战：基于Scikit-Learn, Keras & TensorFlow

机器学习中的数学修炼 左飞(清华大学出版社)

An Introduction to Optimization (Fourth Edition)

end

AI技术交流 + 兴趣讨论：