dijkstra算法过程图解_狄克斯特拉算法的简单解释

简介

狄克斯特拉算法解决了**有向图最短路径**的问题。

戴克斯特拉算法（英语：Dijkstra'salgorithm），又译迪杰斯特拉算法，亦可不音译而称为Dijkstra算法，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法，并于3年后在期刊上发表。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

基本思路

狄克斯特拉算法包含4个步骤。

(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。

(2) 更新该节点的邻居的开销。

(3) 重复这个过程，直到对图中的每个节点都这样做了。

(4) 计算最终路径。

图解算法

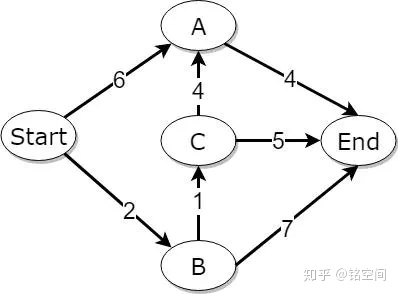
上图中包括6个节点，箭头表示方向，线上的数字表示耗费时间。比如从start到B节点需要花费2个时间单位。但是从B却无法到达Start，因为箭头是有方向的。

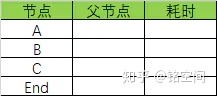
首先根据上图做出一个初始表(父节点代表从哪个节点到达该节点)：

然后从start开始，根据图中的信息更新一下表，由于从start不能直接到达C和End节点，所以耗时为∞(无穷大)，从start到B花费2，从start到A花费6：

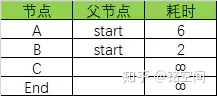
有了这个表我们可以根据算法的步骤往下进行了。

第一步：找出“最便宜”的节点，这里是节点B（只花费了2）：

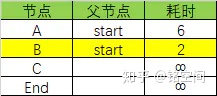
第二步：更新该节点的邻居的开销，根据图从B出发可以到达C和End节点，B目前的消耗2+B到C的消耗1=3（因为要从start开始算花费，所以要把从start到B的花费加上），3小于原来C的消耗∞，所以更新节点C相关的行：

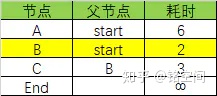
同理，B目前消耗2+B到End的消耗7=9，小于∞，更新End节点行：

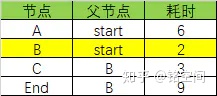
B节点关联的节点已经更新完成，所以B节点不在后面的更新范围之内了：

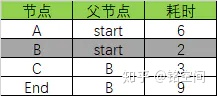
找到下一个消耗最小的节点，那就是C节点：

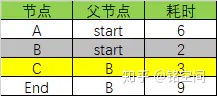
根据C节点的消耗更新关联节点，只有End节点行被更新了，C目前的消耗3+C到end的消耗5=8：

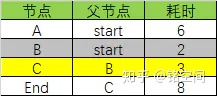
这时候C节点也不在更新节点范围之内了，把C节点置灰：

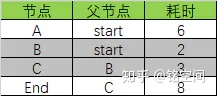
最后只剩下A节点了，根据A节点的消耗没有更新任何行，A节点只能到达End节点，A节点目前的消耗6+A节点到End节点的消耗4=10，由于10大于8所以End节点行不更新：

最终表的数据如下：

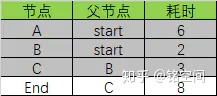
根据最终表，从Start到End的最少消耗是8，路径是Start->B->C->End.这个路径是从后往前推出来的，End<-C<-B<-Start.

代码实现

graph = {}
graph["Start"] = {}
graph["Start"]["A"] = 6
graph["Start"]["B"] = 2
graph["A"] = {}
graph["A"]["End"] = 4
graph["B"] = {}
graph["B"]["C"] = 1
graph["B"]["End"] = 7
graph["C"] = {}
graph["C"]["A"] = 4
graph["C"]["End"] = 5

infinity = float("inf")
costs = {}
costs["A"] = 6
costs["B"] = 2
costs["C"] = infinity
costs["End"] = infinity

parents = {}
parents["A"] = "Start"
parents["B"] = "Start"
parents["C"] = None
parents["End"] = None


def findLowestCostNode(costs, processed):
    lowest_cost = infinity
    lowest_cost_node = None
    for node in costs:
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node

    return lowest_cost_node


def Dijkstra():
    processed = []
    node = findLowestCostNode(costs, processed)
    while node is not None and node != "End":
        cost = costs[node]
        neighbors = graph[node]
        for n in neighbors.keys():
            new_cost = cost + neighbors[n]
            if new_cost < costs[n]:
                costs[n] = new_cost
                parents[n] = node

        processed.append(node)
        node = findLowestCostNode(costs, processed)


Dijkstra()
print(costs)
print(parents)

实际生活中的使用例子

• 地图

如果您曾经尝试查找从一个点/位置到另一点/目的地的距离或路径，或者说从一个城市到另一个城市，或者从您的位置到最近的加油站，这很可能是您遇到的最短路径问题。 用数学术语来说，它是在图中两点之间找到最短的路径，Dijkstra的算法很可能适用于此。

另一个示例是消防员部门想要开发一种系统，该系统可以找到距离最近的消防员部门与被烧房屋之间的最短距离，以避免额外的延迟。 或者，物流公司希望开发一种系统，该系统可以找到仓库和目的地之间最短的距离，以避免额外的花费和时间。 对于此类系统的开发，Dijkstra的算法非常适用。

• 社交网络应用

在许多社交网络应用程序中，推送给特定用户的可能认识的朋友列表非常普遍。您如何看待许多社交媒体公司如何有效地实现此功能，特别是当系统拥有十亿用户时。可以使用握手或两个用户之间的连接度，利用Dijkstra算法计算出来。

许多社交网络应用程序都基于六个分离度，这是用两个用户之间的握手次数来衡量的距离。即使用户的平均朋友数量不大，从算法复杂性的角度来看，找到用户之间最短路径的问题也非常复杂。

• 电话网

在电话网络中，每条线都有带宽bw。 我们想将电话路由到最高带宽。传输线的带宽是该线路可以支持的最高频率。 通常，如果在某条线路中信号的频率较高，则该线路会降低信号的频率。带宽表示线路可以传输的信息量。

如果我们将一个城市想象成一个图形，则顶点代表交换站，边代表传输线，边的权重代表bw。 因此，它可以归为最短距离问题，Dijkstra非常适用。