c语言数组统计结果直方图,信息熵应用随笔2：直方图详解

一、直方图的基本概念

在上文中介绍了，要计算联合熵，可以借助直方图提供的概率密度估计结果。

直方图既是一种精确表示数值型数据分布的统计图。从更一般的数学意义看，直方图也是一种不预先设定概率分布模型，只利用数据本身，进行概率密度估计的算法。属于统计学中非参数估计的基础算法。

直方图也有很多种，用得最多的一维频率直方图。虽然这种直方图看起来跟条形图(bar graph)差不多，但是条形图目的是关联两个数据维度，而直方图只涉及一个数据维度。要构建一维频率直方图，大致分为如下几步：

第一步，是将一维数据的所有n个样本从小到大升序排列，记作{x1, x2, x3, … , xn}，从而确定其样本取值范围[x1, xn]；

第二步是将整个取值范围划分为一系列连续的间隔，这个间隔被称之为箱(bin)或者bucket(桶)，间隔通常(但不是必须)具有相同的尺寸；

第三步是计算每个间隔中落入了多少个样本(频数)，从而计算出每个间隔中落入样本的频率(频数/n)；

第四步是作图，在直角坐标系上，纵坐标是频率，横坐标是一维数据的数值。在每个间隔上方依据其频率画一个矩形。矩形的高度总和等于1。

直方图概念可以参考维基百科hisogram词条或者百度百科频率直方图词条。直方图绘制中，最重要的工作就是间隔的选取。当样本总数n趋近与无穷而间隔趋近于极小时，频率直方图的阶梯形折线将逼近于概率密度曲线。下文中将统一以bin(箱)来代表间隔。

二、直方图的数学意义

在更一般的数学意义上，直方图是计算落入每个不相交类别(bin)的观察数量的函数mi，而直方图的图形仅仅是表示直方图的一种方式。设bin的宽度为h，bin的数量为k，样本总数为n。这直方图函数m满足如下条件：

样本中最大值为max x, 最小值为min x, 则bin的数量k可以计算如下：

每个设第i个bin内落入的样本数量为mi个，对应的频率fi为：

fi = mi / n

题外话：使用数组将每个bin的上下确界(记作Si和Ii)和对应的频率fi以键值对的形式保存，记为(Si, Ii]: fi，即可将整个直方图的计算结果保存，可随时取出绘制成图形。python的pandas类库就是这么做的。

然而bin的宽度如何选取呢？没有“最佳”的bin宽度，不同的bin宽度可以揭示数据的不同特征。这就是分组数据的精妙之处。有一些经验性的规则可以帮我们。比如：

平方根选择：它取样本总数的平方根并舍入到下一个整数。此方法由Excel、python等许多程序使用

Sturges公式，来自二项式分布，并隐含地假设近似正态分布。它隐含地将箱尺寸基于数据范围，并且如果n  <30 则可能表现不佳  ，因为箱的数量将小 – 小于7 – 并且不太可能在数据中显示趋势。如果数据不是正态分布，它也可能表现不佳。

更多的bin宽度/个数 的经验选择法请参考维基百科hisogram词条。

三、使用Python计算直方图

使用python的pandas类库可以非常轻松地计算一维频率直方图。pandas有两个主要数据结构Series(一维)和DataFrame(二维)。使用Series.value_counts()方法，可以很容易地把某一维数据series的分组频率结果，也保存成series的结构。series结构其实就是个一维数组，只不过其数组下标不一定是递增的自然数列，也可以是指定的索引。关于该函数的详细介绍请参考pandas官方文档pandas.Series.value_counts

PowerShell

In [121]: data = np.random.randint(0, 7, size=50)

In [122]: data

Out[122]:

array([6, 4, 1, 3, 4, 4, 4, 6, 5, 2, 6, 1, 0, 4, 3, 2, 5, 3, 4, 0, 5, 3, 0,

1, 5, 0, 1, 5, 3, 4, 1, 2, 3, 2, 4, 6, 1, 4, 3, 5, 2, 1, 2, 4, 1, 6,

3, 6, 3, 3])

In [123]: s = pd.Series(data)

In [124]: s.value_counts()

Out[124]:

4 10

3 10

1 8

6 6

5 6

2 6

0 4

dtype: int64

//注意，value_counts只统计了频数，没算频率

//要算频率需要归一化，s.value_counts(normalize=True)

//另外bin数量这里取的默认值，如果想指定bin数量，可以写成s.value_counts(bins=10)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

In[121]:data=np.random.randint(0,7,size=50)

In[122]:data

Out[122]:

array([6,4,1,3,4,4,4,6,5,2,6,1,0,4,3,2,5,3,4,0,5,3,0,

1,5,0,1,5,3,4,1,2,3,2,4,6,1,4,3,5,2,1,2,4,1,6,

3,6,3,3])

In[123]:s=pd.Series(data)

In[124]:s.value_counts()

Out[124]:

410

310

18

66

56

26

04

dtype:int64

//注意，value_counts只统计了频数，没算频率

//要算频率需要归一化，s.value_counts(normalize=True)

//另外bin数量这里取的默认值，如果想指定bin数量，可以写成s.value_counts(bins=10)

另外python的numpy类库也有numpy.histogram函数也可以计算直方图统计结果，只是更为底层，它会将频率和bin用两个数组返回。

四、二维联合直方图( 2D Joint Histograms )

之前主要以一维频率直方图为例简单介绍什么是直方图。事实上多个维度也可以计算直方图。先从最简单的二维联合直方图开始介绍。

设有两个样本集X和Y，各有n和m个样本。如果这X与Y各自绘制一维频率直方图，bin的尺寸分别为hx和hy，bin的个数分别是kx, ky。则X与Y构成的二维联合直方图，是一个三维图形：纵轴代表X，横轴代表Y，则二维直方图的bin是一个矩形，面积h = hx * hy。bin的总数k = kx *ky 个。落入每个bin中的样本数或者频率，则以颜色或者Z轴高度表示。

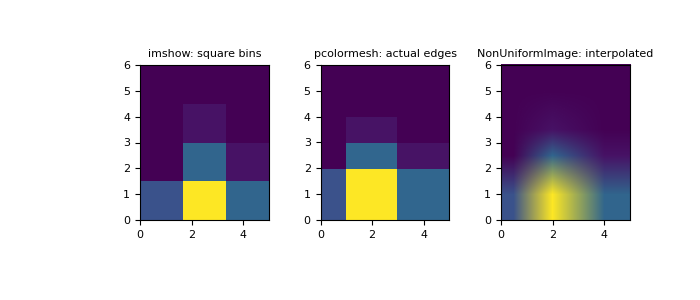
上图是使用python的numpy类库中的numpy.histogram2d 方法来计算二维联合直方图后的结果。这里使用了颜色来表示每个bin中的样本频率。三个小图的不同显示效果是由bin边缘的不同设置造成的。详见numpy官方文档numpy.histogram2d

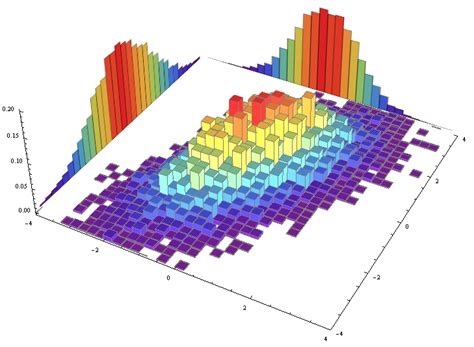
上图是同时使用颜色和Z轴高度来表示每个bin中的样本频率的二维联合直方图。在这个图中，还在X轴和Y轴处还将各自的一维频率直方图展示了出来，更为容易理解。

存储二维联合直方图的重点，是使用标号保存每个bin的位置信息，及bin所对应的频率。故可以用二维数组来存储。简单记作bin[x][y] = f(x,y)， 其中x和y是数组下标， f(x,y)是下标为x,y的bin对应的频率。

五、多维联合直方图( Multivariate Joint Histogram )

我们可以将直方图这一概率密度估计的算法推广到3维或者更高维度，但3维或者更高维度的联合直方图就不好用图形表示了，更多的时候是作为一种记录统计数据的数据结构而存在，可直接帮助我们计算多个数据维度的联合概率分布，稍作变换就可以计算联合熵和条件熵。

站在计算机科学的角度，多维联合直方图的一个重要问题是，如何表示和存储其计算结果。

一个简单的方法是将多变量联合直方图直接存储为多维数组。一维数据的直方图可以存储成一维数组bin[x]=f(x),二维数据的二维联合直方图可以存储为二维数组bin[x][y] = f(x,y)， 以此类推，n维数据可以存储为n维数组bin[x1][x2]…[xn]=f(x1, x2, …, xn)。

有一些C语言类库可以直接计算多维联合直方图，并且可以与python绑定： https://github.com/boostorg/histogram

然而，使用多维数组的内存需求会随着数据维度和bin数量的增加而显著增加。假设有N个数据维度，我们对所有维度都使用B个bin，如果频率也以浮点数进行存储，那么我们就需要B^N个浮点数才能表示这个多维联合直方图。这对存储空间的消耗也指数型增长的。这给我们处理多维联合直方图造成了很大的麻烦。在下一节中将详细介绍存储多维联合直方图的新数据结构。