slam十四讲第四次作业_视觉SLAM十四讲学习笔记（七）

对极约束：

4式和5式都被叫做对级约束，4中的坐标为归一化平面坐标，5中的坐标为像素坐标(齐次坐标)。其中，E=t^R记作本质矩阵，F=K^(-T)EK^(-1)记作基础矩阵。

之前说过单目相机具有尺度不确定性，是由于图像是空间三维物体在二位平面的投影，不具有深度信息(也就是Z轴坐标)。这里从4式、5式中也能看出，在等式两边乘以非零常数等式仍成立，这也被叫做E的尺度等价性。

八点法求解本质矩阵

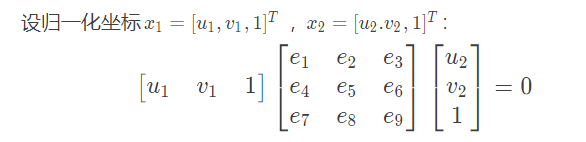
中间的3x3矩阵就是本质矩阵t^R，我们把这个矩阵展开为向量，重写上式：

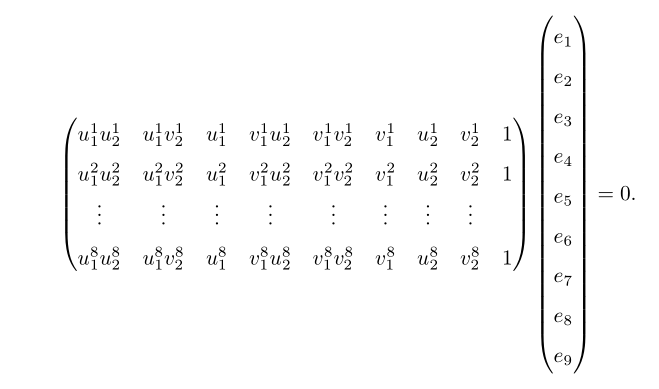
这是一个齐次线性方程组，显然系数矩阵的秩最大为8，但是有9个变量，因此多出一个变量无法约束，就会导致方程组的解不唯一，秩为8时解是一个常数乘以一个向量的形式。

选定一个E进行奇异值分解，即 E=UΣV^T。对于任意一个E，分解得到的t、R组成4组解：

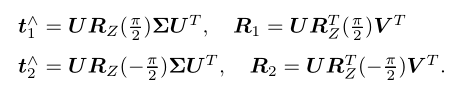
其中R是旋转矩阵，下标Z表示旋转轴是Z轴，pi/2表示旋转的角度。

4种解对应4种不同的相机位姿：

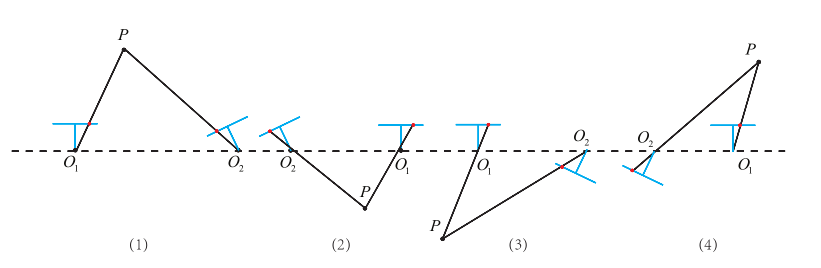
显然，只有第一种解是我们需要的。根据第一种解中三维点的深度都为正，我们选择对应深度都为正的那组解作为奇异值分解的结果。

由于本质矩阵E本身的尺度就是不确定的，所以由奇异值分解得到的旋转、平移也具有尺度不确定性，但旋转矩阵本身是一个行列式为1的正交阵，因此旋转矩阵就可以被确定，这样就只有平移向量的尺度是不确定的。

通常会把初始的平移归一化尺度为1，以后的计算以这个1为单位——这个1的实际大小不确定——导致了单目的尺度不确定性。

实际中特征匹配得到的匹配数往往会多于8对，这个时候可以构建最小二乘问题，然后利用优化算法(如高斯牛顿法、LM法)来得到一个极小值；或者利用RANSAC算法(随意采样一致算法，以后会介绍)，可以从存在误匹配的数据中鲁棒地估计本质矩阵。