判断上三角矩阵_线性代数24——矩阵的对角化和方幂

对角化矩阵 Diagonalizing a matrix

　　假设A有n个线性无关的特征向量

，这些特征向量按列组成矩阵S，S称为

特征向量矩阵。来看一下A乘以S会得到什么：

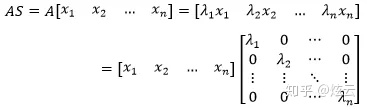
　　最终得到了S和一个以特征值为对角线的对角矩阵的乘积，这个对角矩阵就是特征值矩阵，用

表示：

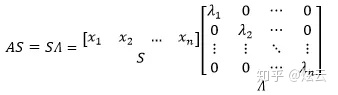
　　没有人关心线性相关的特征向量，上式有意义的前提是S由n个线性无关的特征向量组成，这意味着S可逆，等式两侧可以同时左乘

：

就是对角化的两种方法。需要注意的是，并非所有矩阵A都存在n个线性无关的特征向量，这类矩阵不能对角化。

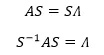
　　矩阵对角化还有另一种表达：

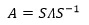
　　我们已经知道了矩阵的LU分解，A=LU；格拉姆-施密特正交化，A=QR；现在又多了一种对角化分解，

之前曾经提到过消元进行行操作和列操作最后会得到“相抵标准型”。现在我们得到的是矩阵的“相似标准形”,它还保有矩阵操作的基本性质——特征值，而相抵标准型只剩下最内核的秩信息还保留着。

矩阵的方幂

　　如果A存在特征值和特征向量，即Ax = λx，那么

的特征值和特征向量是什么？

　　这在上一章的示例中出现过，将Ax = λx的等式两侧同时左乘A就可以表示A的特征向量：