峰度和偏度在金融数据分析中有何应用_做数据分析，为什么要学统计学？

大家好，我是最爱数据分析的勾妹，今天有朋友问我：勾妹发生肾么事了？

对不起走错片场了，是有朋友问我：数据分析干吗要学统计学呢？

在很多人眼里，尤其是刚刚入门数据分析的人眼里，统计学似乎是一门比较枯燥，而且还“没什么用处”的学科。但在数据分析中，统计学还是个非常重要的内容，为什么？

我们先通过一个案例来带感受一下统计学在数据分析中的应用。

案例：

二战期间，德国遭遇了严重的粮食危机，为了应对战时需求，德国政府发布了一个政策：全国的面粉统一由政府管理，政府每天发放固定的面粉量，由指定的工厂进行面包的制作，然后将面包发放到市民手中。

德国政府规定工厂每次发给个人的面包必须为 400g，而在德国柏林住着一位统计学家，发现工厂每天发给自己的面包重量有大有小，这位统计学家统计了一个月以来每天的面包重量，最终制作出一个表格：

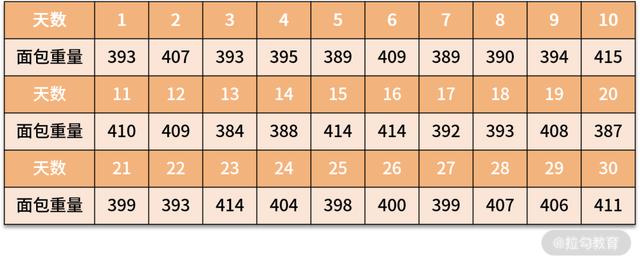
如果没有统计学基础的人看到这个表格可能没有什么头绪，而这位统计学家则看出了工厂的“猫腻”。

因为面包制作的模具不可能是十分精细的，所以制作出来的面包可能是 399g，可能是398g，也可能是 401g、402g，但是根据统计学理论，当样本数据足够多的时候，这些数据一定会符合正态分布，也就是下面这张图：

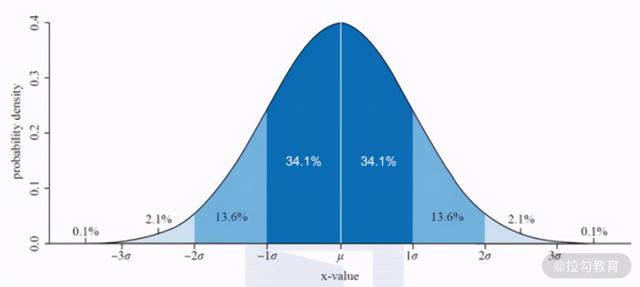
也就是说，68.2% 的数据应该集中于 400g 左右，低于 390g 和高于 410g 的数据应该只占不到 30%。

但是将上图中的数据代入正态分布公式中后就会发现，面包重量的数据发生了偏移(正偏态)，说明该工厂在面包模具上动了手脚，发给市民的面包其实是偏小的，多余的面粉被工厂克扣掉了。

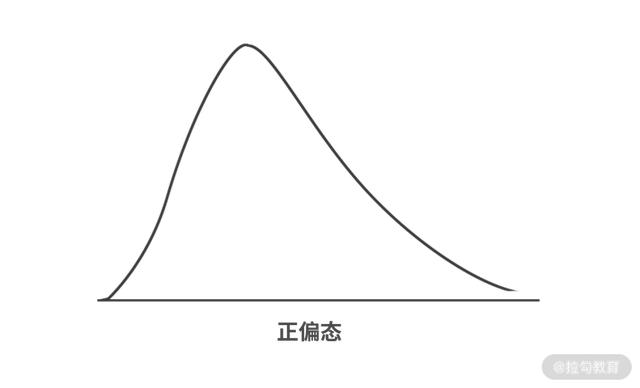
后来调查表明，该工厂确实克扣了大量面粉，故意将模具改小了一点，因此造成了面包重量平均数的下移。这个简单的案例就利用了统计学中一个非常基础的知识——正态分布，这是在我们进行数据分析的时候经常要用到的一个知识。

其实，我们日常用到的平均数、众数、中数、四位数等都是统计学中描述型统计的知识。用通俗的话来解释，就是定量去描述某些数据的特点。

比如销售人员说：“今年我们的销售情况很好，比去年要好很多”，这不叫作描述统计，因为“比去年好”这个特点不是定量的数据，我们可以说“今年的销售额比去年提高 50%”，这就是描述统计。

我们在进行数据分析的时候，一定要记住可量化的指标要量化，不可量化的要定义指标或者公式进行量化。

因为我们要从数据里找结果，而不是从感觉上找差异，最重要的是要避免主观化，不要把经验化的东西带入分析工作中。比如营业额降低，不要想当然地认为就是销售出了问题，要抛开经验和惯性思维，用数据说话。

描述性统计

下面说一下描述性统计的三个分类：集中趋势、离散趋势、分布。

集中趋势

集中趋势就是反映一些数据向某一中心靠拢的程度，也就是说要找到数据的中心点在哪里。集中趋势所要研究的内容，就是某个对象在一定时间和空间条件下的共同性质和一般水平。

常用的指标主要有三个：众数、平均数和分位数。

1)众数

数据的趋势越集中，众数的代表性越好，所以众数不受极端值的影响，但是缺乏唯一性。

2)平均数

平均数代表某个数据集的整体水平，但是平均数有个缺点，就是很容易受极值的影响，比如一家企业告诉你他们公司员工的平均薪资是 50w，结果你去了之后发现大部分人的薪资只有 10w，因为领导层的薪资可能有 100w，直接拉高了整体平均水平。

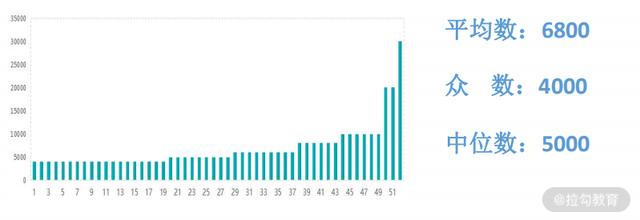
3)分位数

分位数是将某个事件的发生概率按照等分的原则，分成几个等值的点，比如最常见的中位数(即二分位数)，就是将数据平均分为两份。除此之外，常见的分位数还有四分位数、百分位数等。

下面就是四分位数中的五个关键点。

下界：最小值，即第 0%位置的数值；

下四分位数：Q1，即第 25%位置的数值；

中位数：Q2，即第 50%位置的数值；

上四分位数：Q3，即第 75%位置的数值；

上界：最大值，即第 100%位置的数值。

离散趋势

离散趋势反映了各变量远离其中心值的程度，从另一个层面说明了集中趋势量值的代表程度。常用的指标有：极值、方差、标准差、平均差、分位差等。

极值：就是最大值、最小值，代表着数据集合中的上限和下限；

极差：又称“全距”，是一组数据中的最大观测值和最小观测值之差，记作 R。一般情况下，极差越大，离散程度越大，其值越容易受到极端值的影响。

平均差：计算出每个值与平均值的差值，最后计算所有差值的平均值，就是每个数值偏离平均值的程度。

方差：将每个值与平均值的偏差进行平方，最后除以总数据量的值，简单来说就是表示数据与期望值的偏离程度。

方差越大，就意味着每个值与平均值的差值平方和越大、越不稳定、波动越剧烈，代表着数据整体比较分散；

而方差越小，代表着每个值与平均值的差值平方和越小、越稳定、波动越平滑，因此代表着数据整体很集中。

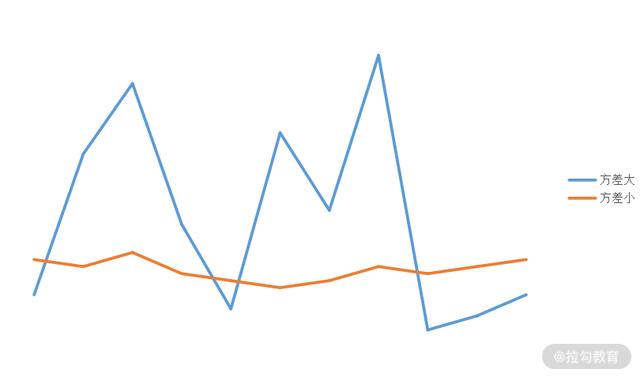
标准差：将方差进行平方根，与方差一样都是表示数据与期望值的偏离程度。开根号是为了方便对比，因为方差计算的是平方值，所以会造成跟检测值差别过大的问题。

分位差：其数值越小表明数据越集中，数值越大表明数据越离散。常用的分位差就是四分位差：四分位差 =(第三个四分位数-第一个四分位数)/2。

分布

我们一般用峰态和偏度来描述数据分布的形态，用来描述数据的整体特征，比如说数据的高峰在哪里、数据大多分布在哪个范围等。

1)峰态

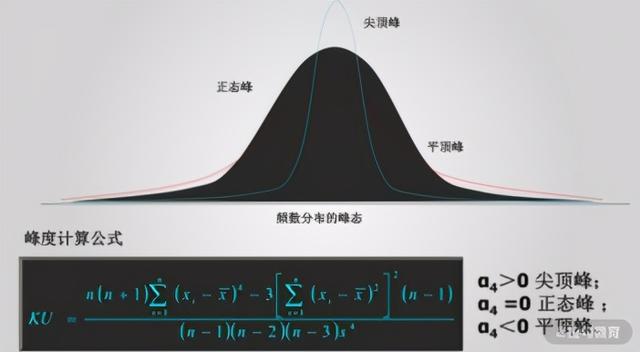
峰态就是概率分布曲线的峰值高低，是尖峰、平顶峰，还是正态峰。

直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言的，用来评估一组数据的分布形状的高低程度的指标。当峰度 =0 时，分布和正态分布基本一致；当峰度 >0 时，分布形态高狭；当峰度 <0 时，分布形态低阔。如下图所示：

2)偏度

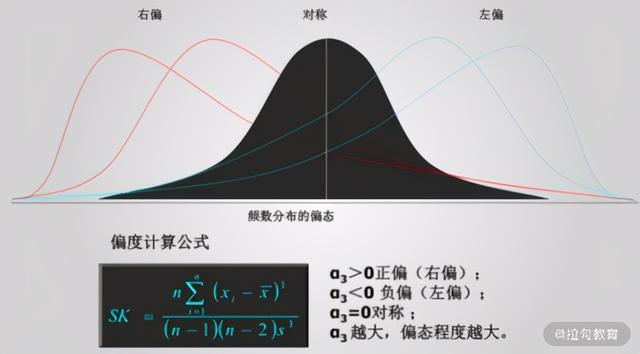
通俗点讲，偏度就是峰值与平均值的偏离程度，是左偏还是右偏。

偏度一般都是用 SK 表示，SK 小于 0，意味着峰值在平均值的左侧，因此称为左偏，也叫负偏；SK 大于 0，意味着峰值在平均值的右侧，因此称为右偏，也叫正偏。

其实我们接触的任何数据，都与概率一词有关，数据分布预测的就是某事件发生的概率，通过分析偏度和峰态，我们能够分析某件事情有没有可能发生，比如预测销售额等。

是不是发现，懂点统计学，在数据分析中还是挺有用的？

本文首发公众号：勾勾谈数据分析

欢迎大家来畅谈数据分析哦[机智]