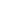快速排序图解_排序算法

1. 快速排序

• 分治思想
• 不稳定
• 时间复杂度：最差O(n^2)，平均O(nlogn)
• 空间复杂度：O(n+1)
• 每次排序设置一个基准点，小于等于基准点的数放到基准点左边，大于等于基准点的数放到基准点右边。

2. 堆排序

• 完全二叉树
• 不稳定
• 时间复杂度：O(nlogn)
• 空间复杂度：O(1)
• 过程：1、初始化堆，从最后一个非叶节点开始调整，将R[0, ..., n-1]构造为堆（交换过程要检查是否保持大/小顶堆性质）2、将当前无序区的堆顶元素R[0]同该区间的最后一个记录交换，然后将新的无序区间调整为新的堆。

3. 冒泡排序

• 稳定
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 临近的数字两两进行比较,按照从小到大或者从大到小的顺序进行交换,这样一趟过去后,最大或最小的数字被交换到了最后一位,然后再从头开始进行两两比较交换,直到倒数第二位时结束。

4. 插入排序

• 稳定
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 插入排序非常类似于整理扑克牌。在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

5. 选择排序

• 不稳定
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 从所有序列中先找到最小的，然后放到第一个位置。之后再看剩余元素中最小的，放到第二个位置……以此类推，就可以完成整个的排序工作了。

6. 归并排序

• 稳定
• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)
• 示意图（图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园）

7. 希尔排序

• 不稳定
• 时间复杂度O(nlogn)~O(n^2)
• 空间复杂度O(1)
• 希尔排序的实质就是分组插入排序，该方法又称缩小增量排序。该方法的基本思想是：把记录按步长 gap 分组（初始gap=n/2），对每组记录采用直接插入排序方法进行排序。随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到1时，整个数据合成为一组，构成一组有序记录，则完成排序。
• https://blog.csdn.net/qq_39207948/article/details/80006224

8. 桶排序

• 稳定
• 时间复杂度：O(n+nlogn-nlogm)，m为桶数
• 空间复杂度：O(n+m)
• 如果相对于同样的N，桶数量M越大，其效率越高，最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M)，如果输入数据非常庞大，而桶的数量也非常多，则空间代价无疑是昂贵的。
• 示意图（【图解数据结构】 一组动画彻底理解桶排序）

9. 其他

内排序：在排序过程中，所有元素调到内存中进行的排序，称为内排序。内排序是排序的基础。内排序效率用比较次数来衡量。按所用策略不同，内排序又可分为插入排序、选择排序、交换排序、归并排序及基数排序等几大类。

外排序：在数据量大的情况下，只能分块排序，但块与块间不能保证有序。外排序用读/写外存的次数来衡量其效率。