leetcode 树相关问题

最新推荐文章于 2023-02-25 09:53:47 发布
最新推荐文章于 2023-02-25 09:53:47 发布
阅读量814 收藏 3
点赞数 1
分类专栏： leetcode 文章标签： 数据结构 二叉树 python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_39940694/article/details/109071612
版权

树相关问题

使用递归和遍历解耦树问题

树的创建与基本的遍历，这是后面大部分问题的基础

创建树

class Node:
    def __init__(self,val):
        self.val = val
        self.right = None
        self.left = None

    def __repr__(self):
        return f'val: {self.val}, left: {self.left}, right: {self.right}'

class Tree:
    def __init__(self):
        self.root = None

    def add_element(self,node_val):
        node = Node(node_val)
        if self.root == None:
            self.root = node
            return
        queue = [self.root]
        while True:
            pop_node = queue.pop(0)
            if pop_node.left is None:
                pop_node.left = node
                return
            else:
                queue.append(pop_node.left)
            if pop_node.right is None:
                pop_node.right = node
                return
            else:
                queue.append(pop_node.right)

新建树结构：

tree =Tree()
for i in range(1,8):
    tree.add_element(i)
  1. pytrhon类内方法__repr__，可以支持类的可视化；
  2. 问题的解耦，Node叶子，包含了值和左右的节点，而Tree树包含了一个队列（先进先出）辅助构建整个树结构。
  3. 树建设好后不需要依靠队列，在内存中依靠指针构成图的数据结构。
  4. Tree类建设好后，该类内的全局变量一直被保存，每次搜索都是从root节点开始，[root]——>pop_node = root——>[root.right,root.left]——>pop_node=root.left——>[root.right,root.left.right,root.left.left]，pop(0)之后会依次追加pop_node的left和right，让每一层满了之后才下一层。
  5. 每次左右都会遍历到，只是有先后次序关系，所以才会让所有的节点都安顺序遍历到。

遍历

bfs

def bfs(self):
    if self.root is None:
        return
    queue = [self.root]
    while queue:
        pop_node = queue.pop(0)
        print(pop_node.val,end=' ')
        if pop_node.left is not None:
            queue.append(pop_node.left)
        if pop_node.right is not None:
            queue.append(pop_node.right)
  1. 与层次化创建一样，依靠一个队列，打印当前节点，把左节点和右节点放进来准备下次的打印。

递归形式的遍历

都是先左再右，前中后只的是根前中后打印。

predfs

根左右

def predfs(self,root):
    if root is None:
        return
    print(root.val,end=' ')
    self.predfs(root.left)
    self.predfs(root.right)
indfs

左根右

def indfs(self,root):
    if root is None:
        return
    self.indfs(root.left)
    print(root.val, end=' ')
    self.indfs(root.right)
afterdfs

左右根

def afterdfs(self,root):
    if root is None:
        return
    self.afterdfs(root.left)
    self.afterdfs(root.right)
    print(root.val, end=' ')

循环形式的遍历（栈）

pre_stack
def pre_stack(self):
    '''
    root left right,因为是stack所以倒着入，出root打印，然后入right，再left
    :return:
    '''
    if self.root is None:
        return
    stack = [self.root]
    while stack:
        pop_node = stack.pop()
        print(pop_node.val,end=' ')
        if pop_node.right is not None:
            stack.append(pop_node.right)
        if pop_node.left is not None:
            stack.append(pop_node.left)
in_stack
def in_stack(self):
    stack = []
    cur = self.root
    #原因为了能让循环开始，开始的时候stack是空的
    while stack or cur:
        while cur：
            stack.append(cur)
            cur = cur.left
        pop_node = stack.pop()
        print(pop_node.val,end=' ')
        cur = pop_node.right
    return
after_stack
 def after_stack(self):
     # left right root ,考虑第一种实现非常方便，所以倒序过来
     if self.root is None:
         return
     stack = [self.root]
     res = []
     while stack:
         pop_node = stack.pop()
         # print(pop_node.val,end=' ')
         res.append(pop_node)
         if pop_node.left is not None:
             stack.append(pop_node.left)
         if pop_node.right is not None:
             stack.append(pop_node.right)
     print(res[::-1])
     return
  1. 建设树的过程是队，遍历使用栈，这里把队和栈的行为表现的非常明白。
    （1）.队列公平的，循环pop(0)依次把pop_node子节点（左、右）的信息入栈，体现了bfs的公平性，本层遍历满后才会继续进行。
    （2）.栈的特点是“先紧着自己人做完的原则”，以前序为例，入栈顺序：right，left。所以，先pop()出栈顶的root，此时left就是当前的root整个循环串接起来，直到把所有关于left的内容都遍历结束，才开始遍历栈底的right（这个right在开始的时候就已经入栈），这里关键是对树的结构依靠了栈的方式进行了遍历，从root的地方把right和left入进来，而后开始循环。注意是出栈的时候才把这个节点的相关节点入栈。
  2. 中序遍历最复杂，关键是这个方法不是先出栈root节点。需要先找到最左边节点。所以除了依靠一个stack，还要依靠一个cur指针。
  3. 内层的while找到最左边的节点后出栈指向该节点的right，再入循环（可能是左子树的右节点），使用cur很妙的地方在于如果没有right接点直接对stack进行pop。代码很自然的完成了left root right的任务（包括了左节点还有右节点的case），所以还是先把整个结构构建起来，细枝末节的任务就容易了。

二叉树的恢复

从前序与中序遍历中恢复二叉树 leetcode 105

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if not preorder or not inorder:
            return
        root = TreeNode(preorder[0])
        index = inorder.index(root.val)
        root.left = self.buildTree(preorder[1:index+1],inorder[:index])
        root.right = self.buildTree(preorder[index+1:],inorder[index+1:])
        return root
  • 必须要有中序这个信息，否则恢复不出来，除非是完全二叉树。
  • 一定要先知道递归的输入和输出是什么，输入是两个列表，输出是输的root

从后序与中序遍历中恢复二叉树 leetcode 106

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        if not inorder or not postorder:
            return
        root = TreeNode(postorder[-1])
        index = inorder.index(root.val)
        root.left = self.buildTree(inorder[:index],postorder[:index])
        root.right =  self.buildTree(inorder[index+1:],postorder[index:-1])
        return root
  • 只要是任意一个list为空则是建树完成。
  • 然后倒换着查看序号即可。

将有序数组转换为二叉搜索树 lc 108

在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if len(nums)==0:
            return 
        mid = len(nums)//2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid+1:])
        return root
  • 是用数组构成树的常规操作，找到一个位置作为root，然后去划分数组变成左右节点。
  • 难点是找到中间这个值划分就可以形成一个平衡的BST。

有序链表转换二叉搜索树 lc 109

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedListToBST(self, head: ListNode) -> TreeNode:
        def findmid(start,end):
            slow = fast = start
            while fast!=end and fast.next!=end:
                slow = slow.next
                fast = fast.next.next
            return slow

        def buildTree(start,end):
            if start==end:
                return
            mid = findmid(start,end)
            root = TreeNode(mid.val)
            root.left = buildTree(start,mid)
            root.right = buildTree(mid.next,end)
            return root
        return buildTree(head,None)
  • 和上一题一样，但是对链表的操作。找重点需要借助快慢指针，其次是建立树的过程是一个显著的二分过程，还是首尾指针，python的list封装太好感觉不出来。

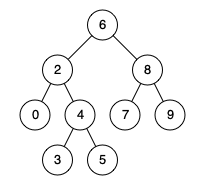
二叉搜索树的最近公共祖先 lc 235

在这里插入图片描述

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root:
            return 
        if p.val>root.val and q.val>root.val:
            return self.lowestCommonAncestor(root.right,p,q)
        elif p.val<root.val and q.val<root.val:
            return self.lowestCommonAncestor(root.left,p,q)
        else:
            return root
  • 因为是BST所以大小是知道的，只不过有两个节点有点麻烦，就同时比较就可以，要不舍弃。
  • 看这个bst的结构确实是如上所述的代码。

两个节点的最近公共节点 leetcode 236

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root:
            return
        if p==root or q==root:
            return root

        # 返回的仅仅是节点，但是不是公共，递归只完成节点的任务
        leftnode = self.lowestCommonAncestor(root.left,p,q)
        rightnode = self.lowestCommonAncestor(root.right,p,q)
        
        # 公共是下面的逻辑,在哪里，如同归并排序，上面分段，下面是排序
        if not leftnode and not rightnode:
            return
        if leftnode and not rightnode:
            return leftnode
        if not leftnode and rightnode:
            return rightnode
        if leftnode and rightnode:
            return root
  • 这种方法和归并排序是一样的，上面负责一路深入下去，在递归之后是具体的最小子操作，就是到了叶子的底部开始比较可能性了。
  • 把问题想清楚，目前的问题是两个节点p，q可能出现在树中的情况是什么，到底了，在一顺，在两边，都不在。
  • 先把问题写出来，缩小问题范围，之后就使用它好了。

最长同值路径 lc 687

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。注意：两个节点之间的路径长度由它们之间的边数表示。

在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def longestUnivaluePath(self, root: TreeNode) -> int:
        def helper(root):
            if not root:
                return 0
            leftCount = helper(root.left)
            rightCount = helper(root.right)
            left,right = 0,0
            if root.left is not None and root.left.val == root.val:
                left = leftCount + 1
            if root.right is not None and root.right.val == root.val:
                right = rightCount + 1
            self.res = max(self.res,left+right)
            return max(left,right)

        self.res = 0
        helper(root)
        return self.res
  • 和上一题有类似，想给出递归的形式和返回值，然后后面利用这个东西，本身返回的是单边的最大值。但是要的res是可以左右之和的打不了一边为0.

归并两个树 lc 617

把两个树对应的位置值相加，形成新的一个树

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if not t1:
            return t2
        if not t2:
            return t1

        root = TreeNode(t1.val+t2.val)
        root.left = self.mergeTrees(t1.left,t2.left)
        root.right = self.mergeTrees(t1.right,t2.right)
        return root

树的回溯问题

二叉树的所有路径 leetcode 257

输入:

   1
 /   \
2     3
 \
  5

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def binaryTreePaths(self, root: TreeNode) -> List[str]:

        def dfs(root,path,res):
            if not root:
                return

            path += str(root.val)
            if not root.left and not root.right:
                res.append(path)
                return
            path+='->'
            dfs(root.left,path,res)
            dfs(root.right, path, res)
        path=''
        res =[]
        dfs(root,path,res)
        return res
  • 最重要的是树的回溯方法，解空间只有两个，左和右，所以不用写循环去遍历，因为只有两个，如果root的左和右都为空的时候，则已经到底了。
  • 输出的格式也有点困难，是字符串，而且还要带个->，所以直接用空字符串去接它，这也是本题目的精髓所在，用结束条件去截止一下。文本也有类似的参考价值。如果还有后续再加上这个东西。这个题目比较特别，如果不是一个的输出，pop很难定位。所以这个特殊问题记住用str。也避免了pop，每一次正好都回去了，而且都是新值。
  • 不用pop因为path是字符串，所以每次的实际地址都不同,python可变变量和不可变变量。

找寻二叉树和为给定数字的所有路径 剑指offer 34

import copy
class Solution:
    def pathSum(selfs,root,sum):
        def dfs(root,path,res,sum):
            if not root:
                return
            if not root.left and not root.right and sum == root.val:
                #判断是树走到头的方法
                #深刻的理解回溯，之前是sum==0是因为不需要走到头，减到0就行了，现在是走到头且最后一个数字是该数字
                path.append(root.val)
                res.append(copy.deepcopy(path))
                path.pop()
                # 注意找到之后就要返回，不继续了
                return
            #现在的解空间只有左和右，所以循环变成两个分开写
            # 方法解耦，这只是加入值，往左右走交给dfs
            path.append(root.val)
            # 这要往下减东西
            dfs(root.left,path,res,sum - root.val)
            path.pop()
            path.append(root.val)
            dfs(root.right, path, res, sum - root.val)
            path.pop()

        path =[]
        res = []
        dfs(root,path,res,sum)
        return res
  • 之前的回溯是所有的解空间，现在解空间就两个，所以不用写循环就直接分开写两次就行了。
  • path是可变的变量，只要加入就要pop，所以上面那涉及到append的就pop。
  • 找到根节点的判断方法。

路径总和 lc 112

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def hasPathSum(self, root: TreeNode, targetSum: int) -> bool:
        if not root:
            return False
        
        def dfs(root,sum_):
            if not root:
                return
            if not root.left and not root.right and sum_==root.val:
                res[0] = True
                return True 
            
            dfs(root.left,sum_-root.val)
            dfs(root.right,sum_-root.val)
        
        res = [False]
        dfs(root,targetSum)
        return res[0]

相同的树 lc 100

给两个树，判断是否是相同的树

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if p and q:
            return p.val == q.val and self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
        return p == q

另一个树的子树 lc 572

在这里插入图片描述在这里插入图片描述

子树 lc 572

判断一个树是否是另一个树的子树

class Solution:
    def isSeemtree(self,s,t):
        if s and t:
            return s.val == t.val and self.isSeemtree(s.left,t.left) and self.isSeemtree(s.right,t.right)
        return s == t
    def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
        if s and t:
        #关键是先判断一下是不是sametree，如果不是的话才左右的递归
            return self.isSeemtree(s,t) or self.isSubtree(s.left,t) or self.isSubtree(s.right,t) 
        return s == t
  • 需要用到sametree，sametree就是看写法是说每一个节点都要一样，如果一个有一个没有那也是False。
  • 子树是same的推广版本，允许部分相同，这就截住了，不一样再往下走，但是也是一定要走到底。不能出现图二的状态。

对称树 lc 101

在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def isSymmetric_(left,right):
            if left and right:
                return left.val == right.val and isSymmetric_(left.left,right.right) and isSymmetric_(left.right,right.left)
            else:
                return left == right
        return isSymmetric_(root,root)
  • 很巧妙的用两个输入，第一次输入的时候也符合这个范式，难点就在这正好同一了。
  • 这一系列题都是一样的，如果没东西了或者一半有就返回相等试试看。

二叉树的层序遍历 II lc 107

层次遍历外面while控制停止，内部的for控制层数
在这里插入图片描述

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        queue = [root]
        res = []
        while queue:
            tmp = []
            for _ in range(len(queue)):
                pop_node = queue.pop(0)
                tmp.append(pop_node.val)
                if pop_node.left:
                    queue.append(pop_node.left)
                if pop_node.right:
                    queue.append(pop_node.right)
            res.append(tmp)
        return res[::-1]
  • 使用队列就是bfs，要不就是dfs。
  • 因为是按照dfs的，所以一层有多个也能收进来。

103. 二叉树的锯齿形层序遍历

z形打印二叉树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        ans = []
        queue = [root]
        turn = 1
        while queue:
            tmp = []
            for _ in range(len(queue)):
                node = queue.pop(0)
                tmp.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            if turn==1:
                ans.append(tmp)
            else:
                ans.append(tmp[::-1])
            turn = -turn
        return ans

找树左下角的值 lc 513

给定一个二叉树，在树的最后一行找到最左边的值。
在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findBottomLeftValue(self, root: TreeNode) -> int:
        if not root:
            return 
        queue = [root]
        while queue:
            for i in range(len(queue)):
                pop_node = queue.pop(0)
                if i == 0:
                    leftmost = pop_node.val
                if pop_node.left:
                    queue.append(pop_node.left)
                if pop_node.right:
                    queue.append(pop_node.right)
        return leftmost
  • 是通过一个简单思路方式取解决，肯定是bfs，最左和最右都很容易实现。

遍历求深度

树的最大深度 流程104

方法1，树大多数是这个套路：

class Solution:
	def maxDepth(self,root):
		if root is None:
			return 0
		else:
			return max(self.maxDepth(root.left),self.maxDepth(root.right))+1

方法2，使用回溯，思路更自然：

class Solution:
    def maxDepth(self,root):
        def dfs(root,deep,res):
            if root == None:
                return
            if root.left == None and root.right == None:
                res.append(deep)
                return
            #很灵魂，意思是如果没到底部那就要+1
            deep += 1
            dfs(root.left,deep,res)
            dfs(root.right,deep,res)
        deep=1
        res=[0]
        dfs(root,deep,res)
        #因为遍历了所有最深的深度，所以返回max即可
        return max(res)

翻转二叉树 leetcode 226

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
    	if not root:
    		return
    	root.right,root.left = self.invertTree(root.left),self.invertTree(root.right)
    	return root
  • 注意这是python的语法，同时让两个内容进行互换。
  • 每一次都是以root为中轴进行翻转，所以依次进行递归。

平衡二叉树 lc 110

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
    #这个有没有这个判断无所谓
        #if not root:
            #return True
        def getDepth(root):
            if not root:
                return 0
            left_height = getDepth(root.left)
            right_height = getDepth(root.right)
			#有可能直接左边或者右边有一支深度失效，无需进一步往下走            
            if left_height == -1 or right_height==-1 or abs(left_height-right_height)>1:
                return -1
            return 1+max(left_height,right_height)
        return getDepth(root)!=-1
  • 二叉树最大深度的变种，只是加多了条件，不平衡的条件。每一次都要网上返回深度。

二叉树的最小深度 lc 111

从叶子节点到根节点的最小深度

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if root.left and root.right:
            return min(self.minDepth(root.left),self.minDepth(root.right))+1
        else:
            return max(self.minDepth(root.left),self.minDepth(root.right))+1
  • 这个题目是理解树的问题，如果有两个叶子节点的话那肯定是两边都是最短的+1。
  • 如果变成单边了，那最短的，思考为一个完整的单支，则是最长+1。

二叉树的直径 lc 543

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

class Solution:
    def diameterOfBinaryTree(self, root):
        res = 0

        def maxDiameter(root):
            nonlocal res
            if not root:
                return 0
            
            l = maxDiameter(root.left)
            r = maxDiameter(root.right)
            res = max(res, l + r)
            return max(l, r) + 1
        
        maxDiameter(root)
        return res
        
#我习惯的写法
class Solution:
    def diameterOfBinaryTree(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """

        res = [0]
        def maxDiameter(root,res):
            if not root:
                return 0
            
            l = maxDiameter(root.left,res)
            r = maxDiameter(root.right,res)
            res[0] = max(res[0], l + r)
            return max(l, r) + 1
        
        maxDiameter(root,res)
        return res[0]
  • 很容易想到还是要计算深度的问题，只不过在每次计算出lr之后，都要算一下左右直径之和。
  • 每次的深度都是单边的。只要是深度的就要想到是深度，就是基础的树高度。只不过是如何拼凑在一起。

路径总和 3 lc 437

给定一个二叉树，它的每个结点都存放着一个整数值。找出路径和等于给定数值的路径总数。路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pathSum(self, root: TreeNode, sum: int) -> int:
        if not root:
            return 0
        def dfs(root,sum):
            if not root:
                return 0
            res = 0
            if sum == root.val:
                res+=1
            #这不能return，因为树有正有负，下面还可能直接加成0还是对的。return就停下来了
                # return res
            res+=dfs(root.left,sum-root.val)
            res+=dfs(root.right,sum-root.val)
            #这里不可以这么写
            # res = dfs(root.left,sum-root.val)+dfs(root.right,sum-root.val)
            #可以这么写，因为左边和右边返回的是找到的结果，但是我要的是结果的
            # res += dfs(root.left,sum-root.val)+dfs(root.right,sum-root.val)
            return res
        
        return dfs(root,sum)+self.pathSum(root.left,sum)+self.pathSum(root.right,sum)
  • 与前面的题目不同的是无需从根开始，所以有最下面的递归。
  • 无需到叶子所以不需要root.left和root.right。
  • 最重要的内容：代码上的两个注释，尤其是res是要用来累加的。里面是int变量这样是我写的比较少的，要多思考一下。注意返回的是什么。
  • 如果是递归内部置0，需要不断的给自己加，如果是外部的话也需要加，注意的是每次递归执行的是找到的操作。

左叶子之和 lc 404

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sumOfLeftLeaves(self, root: TreeNode) -> int:
        self.res = 0
        def dfs(root,sign):
            if not root:
                return
            if not root.left and not root.right and sign=='l':
                self.res+=root.val
                return
            #带标记很巧妙，树返回左和右
            dfs(root.left,'l')
            dfs(root.right,'r')

        dfs(root,'')
        return self.res
  • 是很容易想到要找到所有叶子节点，但是不太好找到所谓的“左”，怎么办那？去给带个标记。

二叉树中第二小的节点 lc 671

给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话，那么该节点的值等于两个子节点中较小的一个。
更正式地说，root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树，你需要输出所有节点中的第二小的值。如果第二小的值不存在的话，输出 -1 。

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findSecondMinimumValue(self, root: TreeNode) -> int:
    #这个min_val是当前最小值，需要return一个比该值大的值
        def helper(root,min_val):
            if not root:
                return -1
#每一次都优先去判断一下该值的关系
            if root.val > min_val:
                return root.val
#递归好思考之后的具体操作,每一枝都会有他的左右，即树的结构。            
            left = helper(root.left,min_val)
            right = helper(root.right,min_val)
#这是实质性的操作，找到左右之后要如果是有一个为空返回对侧，要不就返回两支的min
            if left==-1:
                return right
            if right==-1:
                return left
#每次都返回了左和右枝的最小值，但是还要求该最小值比当前的root.val大，所以min_val是不需要被改变的，一直是当前的这个值
            return min(left,right)
		
        return helper(root,root.val)
  • 简单的思路是直接找左边最小和右边最小的，但是都要比root大才是输出。

BST

修剪二叉搜索树 lc 669

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
        if not root:
            return
        root.left = self.trimBST(root.left,low,high)
        root.right = self.trimBST(root.right,low,high)
        if root.val>high:
            return root.left
        elif root.val<low:
            return root.right
        return root
  • 递归的思路，去左边右边取得一半的内容，然后得到内容后进行判断。

二叉搜索树中第K小的元素 lc 230

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

class Solution:
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        if not root:
            return
        cur = root
        stack = []
        cnt = 0
        while cur or stack:
            while cur:
                stack.append(cur)
                cur = cur.left
            popNode = stack.pop()
            cnt+=1
            if cnt==k:
                return popNode.val
            cur = popNode.right


#递归写法
class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        res = []
        def indfs(root):
            if root is None:
                return
            indfs(root.left)
            res.append(root.val)
            indfs(root.right)
        indfs(root)
        return res[k-1]
  • BST中序查找就是顺序，左中右，而且是升序，BST最重要的性质，所以直接找到然后去找k-1就可以。

把二叉搜索树转换为累加树 lc 538

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        self.add = 0
        if not root:
            return 
        def reverse_inorder(root):
            if not root:
                return 
            reverse_inorder(root.right)
            self.add+=root.val
            root.val = self.add
            reverse_inorder(root.left)
        reverse_inorder(root)
        return root
  • 累加树是指当前节点加上所有比当前节点值小的值，如上图，BST的中序是升序，所以找它的逆序则是降序，每个位置位置都是加上自己当前的值，一路加下去，也不用dp，因为是单调的。直接在当前节点去改变值即可。
  • 这个题目乍一想太复杂，如果展开弄规则太多。是一个应用性质的题目。

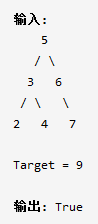
两数之和 IV - 输入 BST lc 653

给定一个二叉搜索树和一个目标结果，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。
在这里插入图片描述

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findTarget(self, root: TreeNode, k: int) -> bool:
        if not root:
            return False
       #注意第一次遍历的时候是空，没有节点被遍历     
        marked = set()
        stack = [root]

        while stack:
            pop_node = stack.pop()
            if pop_node:
                if k-pop_node.val in marked:
                    return True
                # 两数之和就是这个模版
                marked.add(pop_node.val)
                if pop_node.left:
                    stack.append(pop_node.left)
                if pop_node.right:
                    stack.append(pop_node.right)
        return False


# 两数之和，和开平方有点类似不完全一样
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        marked = set()
        for i in range(len(nums)):
            if target-nums[i] in marked:
                return [i,nums.index(target-nums[i])]
            marked.add(nums[i])

求树（BST）的差值最小的值 lc 530

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

class Solution:
    def getMinimumDifference(self, root: TreeNode) -> int:
        if not root:
            return

        l = []
        def indfs(root):
            if root is None:
                return
            indfs(root.left)
            l.append(root.val)
            indfs(root.right)
        indfs(root)

        #想法是中序遍历之后两两是最接近的，所以让两两做差
        min_val = float('inf')
        for i in range(1,len(l)):
            min_val = min(min_val,abs(l[i]-l[i-1]))
        return min_val
        #没必要这样浪费空间和时间。
        # l1 = [l[i] for i in range(1,len(l))]+[0]
        # l2 = [abs(l[i]-l1[i]) for i in range(len(l))]
        # return min(l2)
  • 求最小正好是两两是最小的，但是问题是没必要再开空间，直接每一次后面减去前面ok。
  • 求出来最小的，然后去遍历即可。

二叉搜索树中的众数 lc 501

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

#下面这个是通解，任意二叉树
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def findMode(self, root: TreeNode) -> List[int]:
	    if not root:
	        return
	    stack = [root]
	    adict = {}
	    while stack:
	        pop_node = stack.pop()
	        if pop_node.val not in adict:
	            adict[pop_node.val] = 1
	        else:
	            adict[pop_node.val]+=1
	        if pop_node.left:
	            stack.append(pop_node.left)
	        if pop_node.right:
	            stack.append(pop_node.right)
	    max_val = float('-inf')
	    for k,v in adict.items():
	        max_val = max(max_val,v)
	    res = []
	    for k,v in adict.items():
	        if v==max_val:
	            res.append(k)
	    return res

dp 打家劫舍 III lc 337

树，取root就不能取子节点，取子节点就不能取根。

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def rob(self, root: TreeNode) -> int:
        if not root:
            return 0
        def postdfs(root):
            if not root:
                return [0,0]
            left = postdfs(root.left)
            right = postdfs(root.right)
            val = [0,0]
            val[0] = max(left[0],left[1])+max(right[0],right[1])
            val[1] = left[0]+right[0]+root.val
            return val
        res = postdfs(root)
        return max(res)

#第二种解法
	def rob(self, root: TreeNode) -> int:
        if not root:
            return 0
        ns = {}
        s = {}
        def dfs(root):
            if not root:
                return
            dfs(root.left)
            dfs(root.right)
            s[root] = ns.get(root.left,0)+ns.get(root.right,0)+root.val
            ns[root] = max(s.get(root.left,0),ns.get(root.left,0))+ max(s.get(root.right,0),ns.get(root.right,0))
        dfs(root)
        return max(s[root],ns[root])
  • 和背包也有点像。后续遍历，原因是左右之后汇总在root上做抉择。
  • 因为是一个list，所以对左右节点会有选和不选，不是打家劫舍1的操作。不同点在此。

不同的二叉搜索树 II lc 95

给定一个整数 n，生成所有由 1 … n 为节点所组成的 二叉搜索树 。
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def generateTrees(self, n: int) -> List[TreeNode]:
        if n == 0:
            return []

        def helper(start,end):
            res = []
            if start>end:
                res.append(None)
                return res
            for i in range(start,end+1):
                leftlist = helper(start,i-1)
                rightlist = helper(i+1,end)
                for l in leftlist:
                    for r in rightlist:
                        root = TreeNode(i)
                        root.left = l
                        root.right = r
                        res.append(root)
            return res
        return helper(1,n)

Trie

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。 lc 208

Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 true
trie.search(“app”); // 返回 false
trie.startsWith(“app”); // 返回 true
trie.insert(“app”);
trie.search(“app”); // 返回 true

在这里插入图片描述

class  trie_node:
    def __init__(self):
        #每一个圈是一个dic，key是字母，v是指下去的节点
        self.children = dict()
        #不一定是最终的单词
        self.vaild = False

class Trie:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.root = trie_node()

    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        1.从root开始；
        2.如果一条边存在，顺着该边到下一个节点；
        3.如果边不存在则创建这个边；
        4.单词输入结束，vail=True
        """
        node = self.root
        for i in word:
            if i not in node.children:
            #跟常规的树的感觉不一样，但是也是类似的索引
                node.children[i] = trie_node()
            #存在就去这个节点指向的内容，不存在也创造出来了，可以过来了
            node = node.children[i]
        node.vaild = True

    def search(self, word: str) -> bool:
        """
        Returns if the word is in the trie.
        1.从root开始；
        2.如果一条边存在，顺着该边到下一个节点；
        3.如果边不存在return False
        4.单词输入结束，vail=True
        """
        node = self.root
        for i in word:
            if i not in node.children:
                return False
            node = node.children[i]
        return node.vaild

    def startsWith(self, prefix: str) -> bool:
        """
        Returns if there is any word in the trie that starts with the given prefix.
        """
        node = self.root
        for i in prefix:
            if i not in node.children:
                return False
            node = node.children[i]
        return True



# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
  • 回忆一下我们之前学的前缀树的操作，该树是通过字典的形式维护一个树结构。每次每个节点都有一个是不是最终位置的标识符。
  • 最顶端的是空。每个节点都指向下一堆东西。看插入那段代码，字典里存的是下一个节点。
  • dict[字符]=类

键值映射 lc 677

实现一个 MapSum 类，支持两个方法，insert 和 sum：

在这里插入图片描述

class Node(object):
    def __init__(self, count = 0):
        self.children = collections.defaultdict(Node)
        self.count = count
        
class MapSum(object):

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.root = Node()
        self.keys = {}

    def insert(self, key, val):
        """
        :type key: str
        :type val: int
        :rtype: void
        """
        #这个操作是更新，可能要把之前的key的值更新一个新的数值，如果不是更新则是插入了一个新的值。
        delta = val - self.keys.get(key, 0)
        # 更新保存键值对的keys
        self.keys[key] = val
        
        curr = self.root
        # 更新节点的count
        curr.count += delta
        for char in key:
            curr = curr.children[char]
            curr.count += delta

    def sum(self, prefix):
        """
        :type prefix: str
        :rtype: int
        """
        curr = self.root
        for char in prefix:
            if char not in curr.children:
                return 0
            curr = curr.children[char]
        return curr.count

# Your MapSum object will be instantiated and called as such:
# obj = MapSum()
# obj.insert(key,val)
# param_2 = obj.sum(prefix)
  • 一种比较特殊的数据结构。
短迪大魔王
关注
  • 1
    点赞
  • 踩
  • 3
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
树的定义和遍历
DLzhaohongrui的博客
01-06 115
树是一种数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。（1）每个元素称为节点（node）。（2）有一个特定的节点被称为根节点或树根（root）。
Leetcode 107. 二叉树的层次遍历 II
MD
11-21 85
文章目录问题描述解题报告实现代码 问题描述 解题报告 实现代码 class Solution { public: vector<vector<int>> levelOrderBottom(TreeNode* root) { vector<vector<int>> ans; vector<vector...
数据结构——树的定义、存储与遍历(c语言)
x18037177724的博客
02-25 1531
1.有且只有一个称为根的节点；2.有若干个互不相交的子树，这些子树本身也是一棵树；3.由节点和边组组成的；4.每个节点只有一个父节点，可以有无数个子节点（除了根节点）。
逆元的几种求法（扩展欧几里得，费马小定理或欧拉定理，特例，打表等）
热门推荐
魔笛手的博客
08-04 4万+
乘法逆元 对于缩系中的元素，每个数a均有唯一的与之对应的乘法逆元x，使得ax≡1(mod n) 一个数有逆元的充分必要条件是gcd(a,n)=1，此时逆元唯一存在 逆元的含义：模n意义下，1个数a如果有逆元x，那么除以a相当于乘以x。 下面给出求逆元的几种方法： 1.扩展欧几里得 给定模数m，求a的逆相当于求解ax=1(mod m) 这个方程可以转化为ax-my=
乘法逆元的具体求法
umalaka的博客
01-23 258
费马小定理求逆元 费马小定理：a是不能被质数p整除的正整数，则有 a^(p-1) ≡ 1 (mod p)求a关于p的乘法逆元，即为a*c≡ 1 (mod p),那么a^(p-2)就是a的逆元 Code123456789101112131415LL quickpow(LL x,LL n,LL Mod){ LL ans=1; x%...
Tcloser#leetcode-prectice#哈夫曼树1
07-25
① 对于给定的n个权值{W，w2，.. wn}, 构造出具有n棵叉树的森林F={ T, T,, .... T}，其中每棵.1叉树T均只有一个带有权值w的根结点
leetcode:leetcode中的一些问题
04-13
密码该存储库主要记录有关leetcode的一些问题。 我的有详细的介绍。 二进制搜索，，。 树，，。
LeetCode上经典面试问题Java语言实现
12-21
这是个人搜集的LeetCode上一些经典面试问题的Java语言实现，涉及数组、链表、堆栈、队列、二叉树、并查集、字典树等15个维度，供各位学习参考使用！
LeetCode解题总结
10-09
LeetCode解题总结 1. 数组 1.1 从有序数组中删除重复元素 1.2 在排序数组被旋转后进行查找 1.3 寻找两个排序数组的中位数 1.4 最长连续序列 1.5 累加和 1.6 移除数组中指定值 1.7 下一个排列 1.8 第n个全排列 1.9 ...
leetcode中文版-LeetCode:算法练习：LeetCode问题、LeetCode每周竞赛等
06-29
树的路径相关，递归的过程之中不断更新全局变量 剪枝 二叉搜索树 数学： 概率：洗牌算法、蓄水池抽样、蒙特卡洛 数论：素数，最小公倍数，最大公约数 位运算：异或，与的巧妙用法 特殊的数：有效数字（状态机），第n...
有关逆元的求法
algzjh的博客
01-03 576
详见Modular multiplicative inverse
【数据结构和算法】全面剖析树的各类遍历方法
ZeeCoder
08-11 1万+
面试中常考到树的前序，中序，后序和层序遍历，这篇博文就带你深度剖析一下二叉树的各类遍历算法的实现二叉树的遍历主要有四种，前序、中序、后序和层序遍历的实现方式主要是：递归和非递归递归遍历的实现非常容易，非递归的实现需要用到栈，难度系数要高一点。一、二叉树节点的定义二叉树的每个节点由节点值、左子树和右子树组成。class TreeNode{ public: int val; TreeNo
二值图像求取连通域算法
weixin_30604651的博客
11-03 1071
一幅图像二值化处理后往往包含多个区域，需要通过标记把它们分别提取出来。标记分割后图像中各区域的简单而有效的方法是检查各像素与其相邻像素的连通性。 在二值图像中，背景区像素的值为0，目标区域的像素值为1。假设对一幅图像从左向右，从上向下进行扫描，要标记当前正被扫描的像素需要检查它与在它之前被扫描到的若干个近邻像素的连通性。 考虑4连通的情形。对图像进行逐像素扫描。 假如当前像素值为0...
树类的定义和遍历
学习，记录，总结 的专栏
12-15 1326
实现树类的定义，结点的增删，以及先根，后根，层序周游遍历 #include #include using namespace std; template class Tree; //声明树类 template class TreeNode { friend class Tree; private: T m_Value;
无数种求逆元的方法总结
xuanweiace的博客
07-29 1万+
乘法逆元 对于缩系中的元素，每个数a均有唯一的与之对应的乘法逆元x，使得ax≡1(mod n) 一个数有逆元的充分必要条件是gcd(a,n)=1，此时逆元唯一存在 逆元的含义：模n意义下，1个数a如果有逆元x，那么除以a相当于乘以x。 下面给出求逆元的几种方法： 1.扩展欧几里得 给定模数m，求a的逆相当于求解ax=1(mod m) 这个方程可以转化为ax-my=1 然后套用求二...
重建二叉树和遍历二叉树
blue‘s blog
06-10 115
class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None #1.由中序和前序重建二叉树，输出后序 #中：GDHBEAFC 前：ABDGHECF def recreateTree(preorder,i...
LeetCode 二叉树专题 (1)二叉树知识 和 解题框架
baidu_38689052的博客
07-10 268
算法题中树相关的题目是相对比较难的，同时在开始刷算法题时，也最好先从树型题刷起，因为他的解题思想对以后各种题型都是有帮助的。在对与树型相关的题目我们多练习发现还是有解题框架我们可以套用的。本篇先简单介绍一下树型数据结构的定义，然后讲解下树形题的大致解体思路。在面对一个数据结构时，我们要看他的存储和遍历，毕竟数据结构就是为了方便我们遍历而存在的。 树定义 表示逻辑上的一对多关系，每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个..
树的基本定义和遍历
我要好好当个计院狗
10-05 109
#include<stdio.h> #include<stdlib.h> //二叉树的链式存储 typedef struct BiNode{ int data; struct BiNode *lchild,*rchild; }BiNode,*BiTree; //定义一棵树 BiTree root = NULL; void Visit(BiNode *N){ printf("%d\n",N->data); } void PreOrder(BiTree ..
python二叉树遍历、求深度、已知前序中序 求树 求后序
遇到问题写下来，为了以后方便查啊～
04-19 4447
已知前序中序 求二叉树
leetcode 线段树
最新发布
10-03
线段树是一种二叉搜索树，用于处理区间查询的数据结构。它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。线段树是一棵平衡二叉树，最后的子节点数目为N，即为整个线段区间的长度。线段树的结构可以使用二叉树的表示方法来实现。建立线段树时，可以根据给定的区间范围递归地构建树的节点，＊＊＊. 线段树的应用有哪些？ 4. 线段树的时间复杂度是多少？ 5. 线段树和区间树有何区别？ 请注意，以上回答仅针对引用内容中与线段树相关的部分。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值