
最近蛮多同学问我数学的解题思想和方法的,我在这里写篇文章统一回答一下大家
面对我们高考,掌握数学就意味着要善于解题。
每当我们遇到一个新问题,就很自然的想到利用自己熟悉的解题方法去“套”,这种“套“的方法只是停留在解出来的层面,想要真正的提出新想法以及巧妙的解法那只有对数学思想、数学方法理解透彻及融会贯通。
高考试题最注重的是数学思想方法,特别是那些难题考查的就是这方面的能力,往往我们对这类题进行解答时其过程都包含着重要的数学思想方法。所以我们在整个高中就要有意识地培养起数学思想,并且利用这些方法去分析问题解决问题,培养起的这种能力就是我们平时说的数学思维或者叫数学修养。
那么常见的数学思想有哪几种呢?
① 最常见的方法有:配方法、换元法、待定系数法、数学归纳法、参数法、消去法(或者叫消元法)等;
② 常见的逻辑方法有:分析法、综合法、反证法、归纳法、演绎法等;
③ 常见的思维方法有:观察与分析、概括与抽象、分析与综合、特殊与一般、类比、归纳和演绎等;
④ 常见的数学思想有:函数与方程思想、数形结合思想、分类讨论思想、转化(化归)思想等。
那么数学思想方法和数学基础知识对比起来有什么区别呢?
数学思想明显有着比数学基础更高的层次当然啦,它在平时考试中所占的比重和地位也是比基础知识要高的。
为什么会这样呢?先来说说数学知识的实质以及数学思想的实质
数学知识实质是一些数学公式,数学概念以及书本里由一些文字和符号来记录和描述数学内容,数学知识的保值性并不是很好,这种东西会随着时间的推移,记忆力的减退,将来就很有可能淡记。
数学思想方法实质上就是我们平时说的数学意识,这个东西就很虚无缥缈,我们往往就只能说数学意思只能领会不能言传(这个就很像打王者时的意识差不多,就是感觉这个草丛里就是有人,原因嘛又不好说出来),这种思维就是慢慢在对数学问题的认识、处理和解决中练就而来的,好不夸张的说掌握了数学思想方法,你不单单能受用一阵子,而是受用一辈子,即使是将来数学知识淡记了,而数学思想方法还是刻在骨子里。
接下来就是简单的介绍一下常用的数学基本方法:配方法、换元法、待定系数法
再介绍简单介绍常用的数学思想:函数与方程思想、数形结合思想、分类讨论思想。
一.配方法
配方法就是我们平时说的“完全平方”,通过配方找到已知和未知的联系,从而化繁为简。何时配方,需要我们适当预测,并且合理运用“裂项”与“添项”、“配”与“凑”的技巧,从而完成配方。有时也将其称为“凑配法”。
最常见的配方是进行恒等变形,使数学式子出现完全平方。它主要适用于:已知或者未知中含有二次方程、二次不等式、二次函数、二次代数式的讨论与求解,或者缺xy项的二次曲线的平移变换等问题。
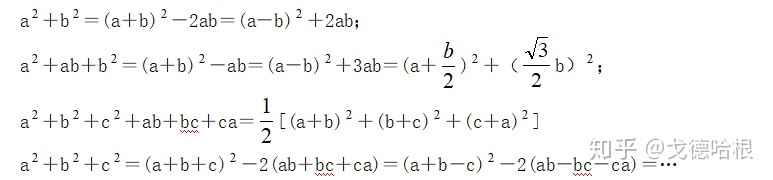









 本文探讨了高中数学中的重要解题思想和方法,包括配方法、换元法和待定系数法。强调了数学思想在解题中的核心地位,指出它们比基础知识更具层次性和重要性。文章详细解释了每种方法的实质、应用场景和解题步骤,帮助读者理解和掌握这些方法。
本文探讨了高中数学中的重要解题思想和方法,包括配方法、换元法和待定系数法。强调了数学思想在解题中的核心地位,指出它们比基础知识更具层次性和重要性。文章详细解释了每种方法的实质、应用场景和解题步骤,帮助读者理解和掌握这些方法。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2759
2759

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








