
这是传送门:
fjd小弟:光滑流形初步(1)——一些概念和例子zhuanlan.zhihu.com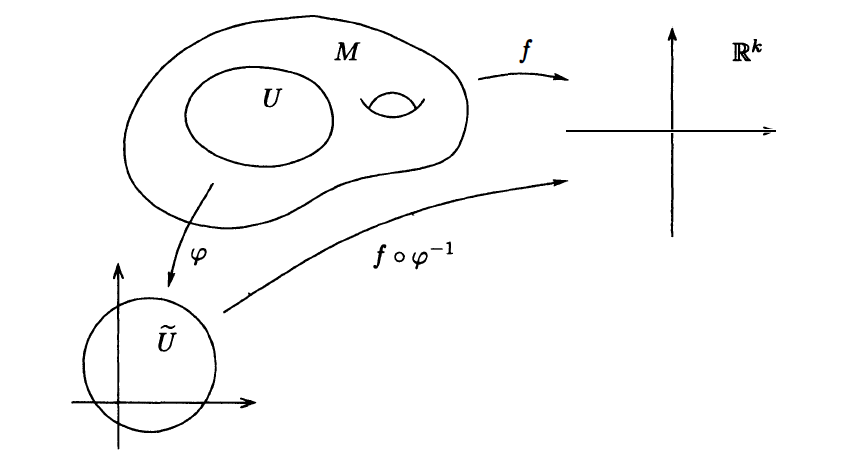
上次讲了流形的一些基本概念,最后也还提到了重要的单位分解定理,这里就先简单叙述一下.
定义(单位分解).上的单位分解是
上的一族光滑函数
,使得:1)
;2)支集族
局部有限;3)
,
.
单位分解想要做的事情,就是将流形从局部过渡到整体,有点儿把每一块局部欧式空间拼接起来的意思,这里不详细讨论.下面的定理断言了单位分解是存在的.
定理(单位分解的存在性).为微分流形,
是
的一个开覆盖,则存在一个从属于
的可数单位分解
,且对
,
是紧的.
尽管这里没有仔细讨论,但单位分解定理在流形论中是十分重要的,它有着广泛的应用,比如用来证明
切向量
下面进入这次的正题,切向量.这是流形论中最重要的内容之一.回想我们过去在欧氏空间中学习的切向量,它可以看作是欧氏空间中某个参数曲面上沿着参数曲线在某点处的切线方向的向量.然而到了一般流形上,向量不再有意义,但直观告诉我们,流形上也应该存在着某种和欧氏空间中切向量所对应的的概念.这时我们从另外一个角度去考察切向量.回顾欧氏空间中的切向量,我们将
定义(函数芽).,在
处的光滑函数
称为在
处有相同的芽,若
在
的某个开邻域内相等.这在
上给出了一个等价关系,两个函数等价当且仅当它们同芽.将等价类称为芽,在
点的芽的集合为
,若
,则用
表示它的芽.函数的加法,数乘,乘法运算在
上诱导了一个
上的代数结构.令
是在![]()
为零的芽的集合,则
是
的理想,用
表示它的
次幂,则
是由
中的元的
重积的所有有限线性组合构成的
的理想,并有递减理想序列
定义(切向量)..
处的切向量
是
的一个线性求导算子,即对
,满足1)
;2)
.记
在
处切向量的集合为
,称为
在
处的切空间.
容易证明,
引理.自然同构于
(
定理.表示对偶空间).
.
注:
这里略去证明,证明过程可以参考GTM94.
大家可以看到,这样定义的切向量看上去是非常抽象的,但用这种方式定义也有它的好处,一个原因是这个定义是内蕴的,它并不依赖于坐标系的选取;另一个原因是它能自然地推广到高阶切向量.事实上,定义切向量还有其它方式.
定义(偏导数与切向量).为光滑流形,
,
为一个以
为坐标的坐标系,对
,定义切向量
:
,这可以理解为
在
点沿坐标
方向的方向导数.
注:可以由切向量的定义验证
微分(切映射)
在上一部分我们主要讨论在流形
定义(微分).为
映射,
,则
在
处的微分(切映射)为线性映射:
,令
,则
为
处的切向量,
定义为
.
看了这个定义似乎顿感头大,但仔细来分析一下这个定义就会觉得这么做也是自然的.
理解这个定义主要是要理解
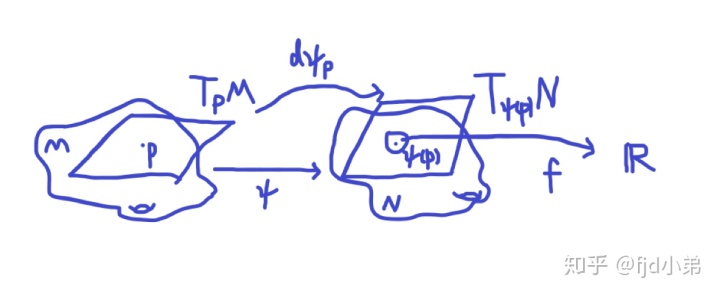
容易验证,
定义(拉回映射).定义为
.
注:设
注:(链式法则)设
注:(光滑曲线定义切向量)这应该是最为直观,也是大家最好理解的切向量的定义方式了.我们称

对于上面曲线切向量所给出的定义,我们有一个很棒的结论:
性质.令为
的,
.若
为对应的光滑曲线,则
.
证明:
本节的最后给出一个有用的定理.
定理.为
的,
连通,且对
,则
为常值映射.
证明:设
这一节的内容刚开始接触时会感到抽象,但如果脑海里能有几何直观,那么这些东西也是相当自然的.为了更好地理解这一部分内容,下次将会给出一些典型的计算切空间、微分的具体例子,然后再介绍一些经典的矩阵群.
fjd小弟:光滑流形初步(3)——一些典型例子zhuanlan.zhihu.com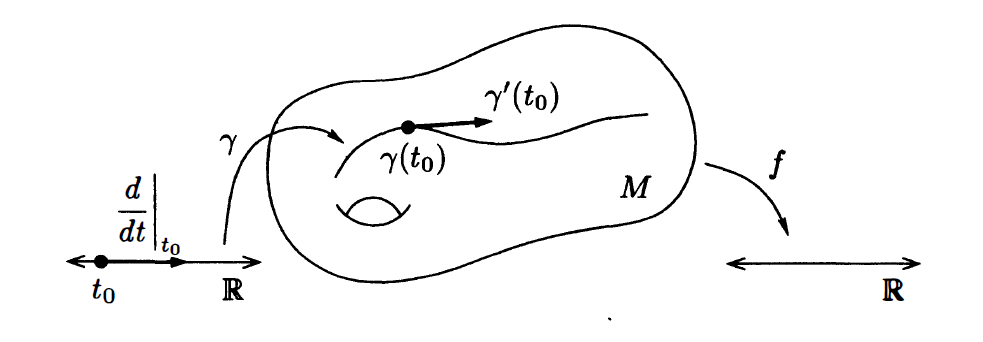




















 1340
1340











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








