算法之动态规划，问题二：带权重的任务安排问题

1 问题的描述

一个任务j在sj开始，并在fj结束;并且每个任务都有权重。
任务相容：任务安排的时间没有重叠
目标：找到最大权重，且相容的任务安排
举例：如下图，可以有如下的活动安排：

a、g
a、h
b、e、h
b、f
b、g
c、f
c、g
c、h
d、h
e、h
一共有10种相容的活动安排，那么谁才是权重最大的一组呢？

2 贪心算法？

（1）：本问题是每个任务带有权重！！！回忆贪心算法求解这个问题时，是不带权重的，若用贪心算法求解该问题，会出现错误。比如：

正如上图看到的，贪心算法选择a、h,显然权重之和2小于b的权重（999）。
（2）：是全部抛弃贪心这种解决问题的思想吗？其实不是的，这里任要求任务按最早结束时间升序排序。
（3）：可以得到一个结论，当每个任务的权重都是1的时候，就退化成的贪心算法了。即：解决这个问题要用到动态规划算法。

3 算法的参数约定及递推式

前提：任务按最早结束时间升序排序！！！

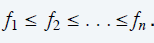
在满足上面的前提下。我们定义两个参数约定:P(j)、OPT(j)

定义：P(j)=与j活动相容的最大的i.其实这就贪心，选了j活动，我就要贪心选一个最大的，是哪个不冲突的最大的活动。
如下图，例如：p(8) = 1, p(7) = 3, p(2) = 0.

算法具体流程：
定义：OPT(j)= 前j个活动权重和最大值（1，2，3...j），也就是说：前j个活动我已经知道最大值了。
目标：OPT(n)，一共n个任务。
显然有两种方案，即（1）选择j活动（2）不选择j活动，动态规划**问题分析是自顶而下的思路**，比如这里从j任务开始分析的，但是算法实现却是自底而上的策略。
case 1:
	如果不选择活动j，原问题蜕化成OPT(j-1)，即从(1,2,3...j-1)中找最优解
case 2:
	如果选择活动j，原问题退化成Wj+OPT(P(j)),即既然选择了j活动，必然下一个活动不能和j活动冲突的最大活动P(j),其中Wj是J活动的权重。
递推如下：

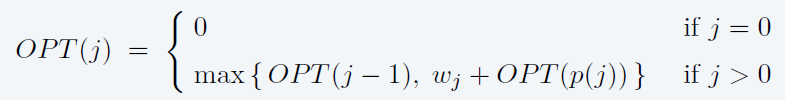
4 算法具体实现

在了解了算法递推式的核心后，我们就可以完整的描述这个过程了。

活动按最早结束时间升序排序，这步我省略了。时间复杂度：O(n log n)
计算每一个P(j)，采用二分查找O(log n），一共n个任务。时间复杂度：O(n log n)
计算每一个OPT(j),即OPT(j) ? Wj+OPT(P(j))
通过结果，回溯有哪些任务

请结合最后的例子，一起阅读！！！

/*****************************************************************************************************
** key: j号task的开始时间，即startArray[j]
** finsh[] && currentIndex: 查找“j号task的开始时间”在j-1号之前的任务的结束时间finishArray[1...j-1]
*****************************************************************************************************/
int binarySereach(int key, int finsh[], int currentIndex)
{
	int low = 1, high = currentIndex;
	while (low <= high) {
		int mid = (low + high) / 2;
		if (key == finsh[mid])									//找到即返回Index
			return mid;
		else if (key < finsh[mid]) {							//key小于所有的finshTime，即没有一个任务相容
			high = mid - 1;
			if (high < low)
				return 0;
		}else{													//key大于所有的finshTime，最大的相容的，即high
			low = mid + 1;
			if (low > high)
				return high;
		}	
	}
	return 0;
}

/***********************************************************
** P(j)怎么计算出来的呢？
** 比如P(8)=5?,这个5是j=8活动的开始时间8到1..7活动的结束时间4，5，6，7，8，9，10，发现是5号元素，
** 也就是，在选了8号活动，最贪心的就是5活动了，6、7活动冲突。
************************************************************/
void DynamicScheduling(TASK_INFO *schedule, int **compute, int taskNum)
{
	int* startArray = new int[taskNum+1];												//将每个任务的开始、结束时间转存下，方便计算P(j)
	int* finishArray = new int[taskNum+1]; 
	for (unsigned int i = 1; i < taskNum+1; i++)
	{
		startArray[i] = schedule[i-1].iStartT;
		finishArray[i] = schedule[i-1].iFinshT;
	}

	//compute P(j) & OPT(j)
	for (unsigned int j = 1; j < taskNum + 1; j++) {
		//P(j)
		compute[0][j] = binarySereach(startArray[j], finishArray, j - 1);

		//OPT(j)：OPT(j) ? Wj+OPT(P(j))
		if (compute[1][j - 1] > schedule[j-1].iWight + compute[1][compute[0][j]])  			//第一个任务信息在0号内存单元的，所以是schedule[j-1].iWight
			compute[1][j] = compute[1][j - 1];
		else
			compute[1][j] = schedule[j-1].iWight + compute[1][compute[0][j]];
	}
	delete[] startArray;						//从理论上讲，new的内存必需要delete才能释放，不知道编译器有优化没？，还是显示的释放下
	delete[] finishArray;
}

注意：
（1）：很明显，程序是自下而上的，因为P(1)算出来了，OPT(1)就出来，如此到最后一个活动。OPT(j)只会用到前面的信息。
（2）：compute[0][]是P(j)；compute[1][]是OPT(j)

5 回溯原问题的解

上面只是计算了最大的权重，但不知道究竟选了哪些活动，为此还要根据之前的信息推出选了哪些活动。

从最直观的角度来讲，OPT(8)=42比OPT(7)=40大，肯定选了8活动的，不选就是40，然而并不是，因为只有两种情况，选/不选。

int g_i = 0;			//返回活动j存在path中
void FindSolution(TASK_INFO *schedule, int **compute, int j, int* path)
{
	if (j == 0)
		return;
	else if (schedule[j - 1].iWight + compute[1][compute[0][j]] > compute[1][j - 1])	//后面值大于前面的，则加入；否则j-1
	{
		path[g_i++] = j;
		return FindSolution(schedule, compute, compute[0][j], path);
	}else
		return FindSolution(schedule, compute, j-1, path);
}

6 案例输出

7 源代码

链接: https://pan.baidu.com/s/1hJR8DdEfrYuenMuFNSkEgQ 提取码: xfju 失效请留言。