半正定矩阵的判定方法_线性代数30——正定矩阵和最小值

我们经常在判定一个函数是否有最小值时使用正定矩阵，正定矩阵和最小值有什么关系呢？

1 判断正定矩阵

给出一个矩阵：

有4个途径可以判定该矩阵是否是正定矩阵（注意这个矩阵的4个元素中有2个b，这是因为正定矩阵是对称矩阵，如果A的次对角线的元素不相等，A就不是对称的，也就没有必要进一步判定是否是正定的）：

1. 所有特征值大于
2. 行列式及左上角的所有
   阶子行列式均为正（1≤k≤n）
3. a > 0,
   （针对2阶矩阵）
4. 对于任意非零向量x，

其中第4个是正定的定义，前3个是用来验证正定的条件。

当y怎样取值时，下面的2阶矩阵是正定的？

根据条件2可知，

时，即y>18时，矩阵是正定的。

如果y=18，则矩阵正好处于正定的临界点上，此时A是奇异矩阵，有一个特征值是0，

。我们称这种处于临界点上的正定矩阵为半正定矩阵。

2 矩阵的二次型

再来看一下

。对于非零向量

x来说， Ax是线性形式，加入

后就变成了含有二次项的形式，比如：

这种形式称为矩阵的二次型。当然

也只有二次型，没有三次型和四次型，即使

x是更多维度的向量也一样，比如当 x是三维向量时，最终结果仍然只含有二次项：

如果对于任意非零向量x来说，矩阵的二次型都大于0，那么这个矩阵是正定矩阵。

y=18时A是半正定矩阵，当

时，其二次型为0：

3二次型的意义

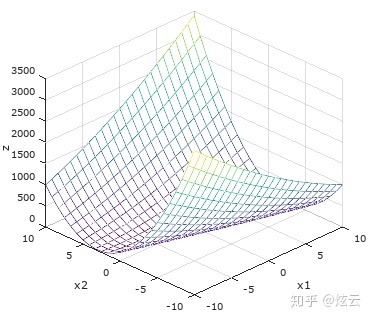
为了画出几何图形，我们以二阶矩阵为例，先看一个非正定矩阵：

它的二次型是

，其几何图形如下：

从图形上看没有最小值点，原点处是一个鞍点，在某个方向看是极大值，同时又是另一个方向的极小值。下图是个经典的鞍点，图形呈马鞍状：

再来看正定矩阵：

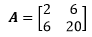
A的二次型是

，图形如下：

回顾本节出现的两个二次型，它们都可以通过配方写成完全平方的形式：

当x,y不全是0时，可以判断第2个二次型一定大于0，第一个就不一定了。此外还可以通过二次型判断临界点是(0, 0)点。

经过配方后的二次型很奇妙，它还可以来自消元：

消元变成了上三角矩阵。A可以通过LU分解成：

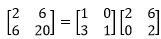
现在把原矩阵、二次型和LU分解放到一块：

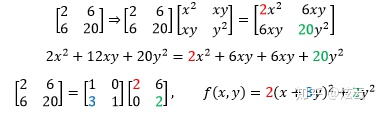
经过消元后的第一个主元是x的系数，第二个主元正是配方项

的系数，如果f大于0，那么这两个系数一定是正值，这也是为什么正定矩阵的

主元一定都为正的原因。

换一个矩阵试试：

其中一个主元是负数，对应的二次型也不能保证一定大于0。

4正定矩阵与最小值

正定矩阵对应的二次型是有最小值的。

4.1 二元函数

判断一元函数是否有最小值，需要判断它的导数和二阶导，同样，多元函数是否有最小值也要根据临界点和二阶导判断。我们在多变量微积分中介绍过怎样判断二元函数的最小值，最小值出现在临界点上：f(x, y)的一个临界点是

，即

且

， f的最小值是根据二阶导数判断的：

对于

来说：

临界点符合最小值的条件，因此(0,0)是

的最小值。这个结论实际上来源于对

A的二阶导矩阵的正定性的判断：

对于二元函数的混合偏导来说，

和

是一样的，因此这个矩阵是对称矩阵。在求得临界点后，根据判定正定矩阵的第3条，只要满足下面的条件，则这个二阶导矩阵是正定矩阵：

4.2 三元函数

现在召唤一个三元矩阵，然后判断它的正定性：

先对其进行消元：

A的主元都大于0，这符合正定矩阵的性质，是一个必要条件。

接下来我们通过子行列式判断A的正定性：

现在可以确定A是正定矩阵。如果进一步求得特征值，则A的3个特征值是：

特征值之和等于A的迹，特征值之积等于A的主元之积。

A是正定矩阵，因此可以判定A的二次型是有最小值的：

用配方法验证：

可以看出最小值的点是(0, 0, 0)。