excel三次样条函数_R相关与回归学习笔记（三十三）——非参数回归模型、样条平滑...

最新推荐文章于 2024-04-28 20:24:11 发布
最新推荐文章于 2024-04-28 20:24:11 发布
阅读量2k 收藏 8
点赞数 1
文章标签： excel三次样条函数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_39962153/article/details/111609694
版权

本笔记中原始数据及代码均来源于李东风先生的R语言教程，在此对李东风先生的无私分享表示感谢。

模型

线性回归模型可以看成非线性回归模型的特例:

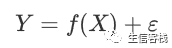
b35d68c7b23875819fdd68a539ac0080.png

其中f(x)为未知的回归函数。 参数方法：假定f(x)具有某种形式，如线性回归，二次多项式回归，指数模型等等

二次多项式回归可以令X1=x,X2=x方， 变成二元回归模型来解决。 指数模型可以令x=lnY, 模型化为z=a+bx。 有一些曲线模型可以通过变换化为线性回归。

在多元情形， 一般的非线性回归模型为

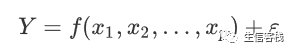
e7ad0d7f00823e255f14af0a97db0486.png

但是这样可选的模型就过于复杂， 难以把握。 比较简单的是不考虑变量之间交互作用的可加模型࿱

最低0.47元/天 解锁文章
weixin_39962153
关注
  • 1
    点赞
  • 踩
  • 8
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
matlab做三次拉格朗日插值多项式_机器人轨迹规划：三次样条曲线（matlab）
weixin_39974409的博客
11-21 2529
写在前面在一些避障的应用场景下，一般都是先在任务空间中对多轴机械臂的末端进行路径规划，得到的是末端的运动路径点数据。这条轨迹只包含位置关系，并没有告诉机器人应该以怎样的速度、加速度运动，这就需要进行带时间参数的轨迹规划处理，也就是对这条空间轨迹进行速度、加速度约束，并且计算运动到每个路点的时间，高级的算法有TOPP等，一般的呢就是贝塞尔、三次准/非/均匀B、五次及三次样条等。下面从最简单的三次样条...
平滑函数
lzj0470的专栏
10-11 1165
http://wenku.baidu.com/view/3f06f988d4d8d15abe234e09.html
ES6箭头函数的使用
Judy-Lin
09-26 203
箭头函数 箭头函数，是ES6 新增的一种函数。箭头函数相当于匿名函数，并且简化了函数定义。 x=>x*x 相当于： function (x){ return x*x; } 箭头函数的使用规则 省略function关键字 如果只有一个参数，可以省略小括号 如果函数只有一条语句，可以省略大括号 如果函数只有一条语句，并且需要返回这条语句的结果，则可以省略return关键字 不可以使用arguments 不可以把自己的this绑定在函数上 不可以用作构造函数 ...
B样条 (折线路径平滑处理)(附MATLAB代码)
最新发布
LJGHZ的博客
04-28 464
总的来说，这段代码实现了三次样条插值的计算过程，从确定插值节点到计算插值结果，最后绘制出了插值曲线。代码中的Bbase包。
SmoothingSplines.jl：Julia中的三次平滑样条曲线
02-04
SmoothingSplines.jl：Julia中的三次平滑样条曲线
三次样条曲线
峻峰飞阳的博客 blog.csdn.net/while0
05-27 7696
阅读 Cocos2d-x 源码的时候，有几个有趣的关于路径运动的 Test Case 之前一直没有时间去研究：ActionCardinalSpline 和 ActionCatmullRom。由于对 Bezier 比较熟悉，所以 ActionBezier 就略过了。于是特地看了一下前两个陌生的名字。之前在博客里记录过几个曲线，一个是贝塞尔曲线，一个是Chaikin曲线以及利萨茹曲线。它们各有特点：贝塞
matlab.rar_spline implement_三次样条函数_三次样条插值_圆滑 matlab_折线 平滑
09-22
在MATLAB中，三次样条插值是一种常用的数据平滑和曲线拟合技术，尤其适用于处理离散数据点，使其在视觉上呈现平滑的连续曲线。本项目着重讲解如何利用MATLAB实现三次样条函数，对折线进行圆滑处理。 首先，我们需要...
样条插值.zip_matlab_三次样条函数_三次样条插值_样条函数_样条插值
07-14
样条插值的研究背景，样条函数的力学意义，三次样条插值多项式的构造，一般的插值问题
matlab---三次样条插值.rar_三次样条_三次样条 matlab_插值_样条函数_编程
07-15
在给定的标题“matlab---三次样条插值.rar”中，关键词“三次样条插值”表明我们将探讨的是使用MATLAB软件实现的三次样条插值技术。描述中提到该方法具有较小的误差和较好的光滑性，这正是三次样条插值的主要优点。 ...
第一种边界条件的三次样条函数插值与微商.rar_三次_三次样条_三次样条函数_样条函数
09-21
三次样条函数，顾名思义，是指由一系列三次多项式函数构成的光滑函数，这些函数在特定点（称为结点）处连接，使得整个函数在整个定义域内连续且三次可微。这种构造方式使得三次样条函数在处理数据插值时能够保持较高...
三次样条曲线.rar_三次样条_三次样条代码_三次样条曲线_曲线平滑_样条曲线
07-14
3种源码，三次样条函数算法C++源代码,用于工程上计算平滑曲线的插值计算.
三次样条插值代码
06-12
#include <iostream> #include <cmath> #include <fstream> using namespace std; class scyt { float *x,*y,*d,*h,*u,*q,*a,*b,*c,*l,*r,*o,*M; int m; float y0,y3; public: scyt(); void qiudao(); void zgf(); void qiujie(); ~scyt(); }; void main() { scyt hello; hello.qiudao(); hello.zgf(); hello.qiujie(); } scyt::scyt() { ifstream fin("三次样条插值.txt"); for(float j;fin>>j;) { m=int(j); break; } x=new float[m]; y=new float[m]; d=new float[m]; h=new float[m-1]; u=new float[m-2]; q=new float[m-2]; a=new float[m-1]; b=new float[m]; c=new float[m-1]; l=new float[m]; r=new float[m-1];//此处的r为追赶法中的u； o=new float[m];//此处o为追赶法中的y M=new float[m];//此处M为追赶法中的x； int jishu=0; for(j;fin>>j;) { if(jishu<=m-1) x[jishu]=j; if(jishu>m-1&&jishu;<2*m) { y[jishu-m]=j; } if(jishu==2*m) { y0=j; } if(jishu==2*m+1) { y3=j; } jishu++; } fin.close(); } void scyt::qiudao() { for(int i=0;i<m-1;i++) { h[i]=x[i+1]-x[i]; } for(i=0;i<m-2;i++) { u[i]=h[i] / (h[i] + h[i+1]); } for(i=0;i<m-2;i++) { q[i]=1-u[i]; } d[0]=6/h[0]*((y[1]-y[0])/h[0]-y0); for(i=1;i<m-1;i++) { d[i]=6/(h[i-1]+h[i])*((y[i+1]-y[i])/h[i]-((y[i]-y[i-1])/h[i-1])); } d[m-1]=6/h[m-2]*(y3-(y[m-1]-y[m-2])/h[m-2]); } void scyt::zgf() { u[m-2]=1; for(int i=0;i<m;i++) { b[i]=2; } c[0]=1; for(i=1;i<m-1;i++) { c[i]=q[i-1]; } //........................................ l[0]=b[0]; for(i=0;i<m-1;i++) { r[i]=c[i] / l[i]; l[i+1]=b[i+1] - (u[i] * r[i]); } o[0]=d[0] / l[0]; for(i=1;i<m;i++) { o[i]=(d[i]-u[i-1]*o[i-1]) / l[i]; } M[m-1]=o[m-1]; for(i=m-2;i>=0;i--) { M[i]=o[i]-r[i] * M[i+1]; } cout<<m<<"个点的导数值分别是："<<endl; for(i=0;i<m;i++) { cout<<"M"<<i+1<<"="; cout<<M[i]<<endl; } //M的值求出。。。。。。追赶法调用完毕 } void scyt::qiujie() { float S; for(;;) { float f; cout<<"请输入待求x的值(输入1000)时退出："; cin>>f; if(f==1000) break; for(int i=0;i<m;i++) { if(f>x[i]&&f<x[i+1]) { S=pow((x[i+1]-f),3)*M[i]/(6*h[i]) + pow(f-x[i],3)*M[i+1]/(6*h[i]) + (x[i+1]-f)*(y[i]-h[i]*h[i]*M[i]/6)/h[i] + (f-x[i])*(y[i+1]-h[i]*h[i]*M[i+1]/6)/h[i]; cout<<"S["<<f<<"]="<<S<<endl; } } } } scyt::~scyt() { delete []x,y,d,h,u,q,a,b,c,l,r,o,M; }
基于R统计软件的三次样条和光滑样条模型数据拟合及预测
拓端研究室TRL
12-11 896
我们通过应用基础函数来变换变量 并使用这些变换后的变量拟合模型， 向模型添加非线性， 使样条曲线能够拟合更光滑。现在我们可以注意到，红线（即“光滑样条线”）更加波动，并且更灵活地拟合数据。因此， 我们需要对数据或变量进行一些转换，以使模型在学习输入X i和输出 Y之间的非线性相互作用时更灵活，更强大。样条线是拟合非线性模型并从数据中学习非线性相互作用的一种方法。我们在光滑样条曲线中的目的是通过添加粗糙度最小化误差函数。上图显示了三次样条曲线的光滑和局部效果。该模型也非常光滑，可以很好地拟合数据。
23种设计模式C++实例之原型模式
寒风的技术博客
12-11 3562
原型模式就是让对象拥有自我拷贝的功能，方便备份对象数据或者创建对象时设置过多的参数。 #include using namespace std; /* * 原型模式：让对象拥有自我复制的功能 * 注意深拷贝和浅拷贝 * */ class Programmer{ public: virtual ~Programmer() {} virtual Programmer*
dispimg函数怎么用_excel中的lookup函数究竟该怎么用？如何才能准确理解它的用法？...
weixin_39736934的博客
11-27 7178
在日常工作中，excel的查找函数可以称得上是函数的精髓之一，因为查找函数单独使用就可以实现很多日常操作需要，更别说很多复杂的函数往往也会嵌套查找函数使用，常用的查找函数有vlookup、index—match、lookup函数等，这些函数非常相似，有些查找选择这些函数任意一个都可以完成，今天小编给大家介绍一下lookup函数的几种用法，这个函数非常灵活，可以在很多种情况下运用。本文概要一：基本正...
三次样条插值实现函数拟合
邮差将军的博客
03-30 6182
数值分析实验——三次样条插值 GoatWu 一、程序摘要 此程序使用 python3.7 语言编写。引入了外部库函数 numpy 作为数学工具解方程，matplotlib 作为画图工具。由于需要多步运行，对不同的参数进行绘图，因此使用了 jupyter-notebook 作为编写工具。 由于用到的函数较多，为了安全起见，此程序将内部函数封装在了 Functions.py 模块中，将接口函数封装在了...
三次样条插值(Cubic Spline Interpolation)及代码实现(C语言)
weixin_34392435的博客
01-26 7433
样条插值是一种工业设计中常用的、得到平滑曲线的一种插值方法，三次样条又是其中用的较为广泛的一种。本篇介绍力求用容易理解的方式，介绍一下三次样条插值的原理，并附C语言的实现代码。 1. 三次样条曲线原理 假设有以下节点     1.1 定义 样条曲线 是一个分段定义的公式。给定n+1个数据点，共有n个区间，三次样条方程满足以下条件： a. 在每个分段区间 （i = 0, 1, …,...
（光滑样条）Smoothing spline的数学推导
热门推荐
qq_40595812的博客
11-08 2万+
Smoothing spline 一般的不加入光滑因子的拟合均方误差如下式： RSS(f,λ)=∑i=1N{yi−f(xi)}2RSS(f,\lambda)=\sum_{i=1}^{N}\left\{y_{i}-f(x_{i})\right\}^{2}RSS(f,λ)=i=1∑N​{yi​−f(xi​)}2 引入λ光滑因子式均方误差\lambda光滑因子式均方误差λ光滑因子式均方误差 RSS(f...
三次样条插值_HHT算法的若干问题及改进方法—— 三次样条插值法
05-21
三次样条插值法是一种常用的插值方法，它可以通过给定的数据点，构造出一个光滑的函数曲线，从而对数据进行插值和拟合。但是，在实际应用中，三次样条插值法可能会面临一些问题，需要进行改进。 以下是三次样条插值法可能面临的若干问题以及改进方法： 1. 插值误差问题：由于三次样条插值法是通过多项式曲线拟合数据点，因此在数据点之间进行插值时，可能会产生插值误差，导致插值结果不准确。解决方法是增加插值节点，即增加数据点的数量，或者采用其他插值方法，如分段线性插值、拉格朗日插值等。 2. 边界条件问题：三次样条插值法需要指定边界条件，如一阶导数、二阶导数等。如果边界条件不合适，可能会导致插值结果不光滑或不连续。解决方法是选择合适的边界条件，例如自然边界条件、弯曲边界条件等。 3. 大数据量问题：当数据点数量非常大时，三次样条插值法的计算量会非常大，导致插值速度变慢。解决方法是采用更高阶的样条插值方法，如五次样条插值法或七次样条插值法，或者采用其他的插值方法，如Kriging插值、径向基函数插值等。 4. 插值函数平滑度问题：三次样条插值法可以构造出光滑的函数曲线，但有时插值函数的平滑度可能不够好，导致插值结果不理想。解决方法是采用其他的插值方法，如样条插值法与小波插值法的结合，或者采用其他的光滑函数，如B样条函数、NURBS曲线等。 总之，三次样条插值法是一种非常实用的插值方法，但在实际应用中可能会面临一些问题，需要根据具体情况选择合适的改进方法。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值