余弦函数导数推导过程_数学漫步：探讨正切函数tanx导数的代数与几何原理

最近我们展示了正弦，余弦函数求导的几何原理，形象直观，更容易理解，今天我们就来讲讲正切函数求导的几何原理，它在一定程度上比正弦，和余弦函数要更为复杂一点。

第一：代数下的推导方式

进行几何推导之前，我们先来欣赏一种优美的代数下的推导方法，这里用到的是分部积分法

首先将tan=sinX/cosX，运用分部积分法，我们很容易得到如下结果

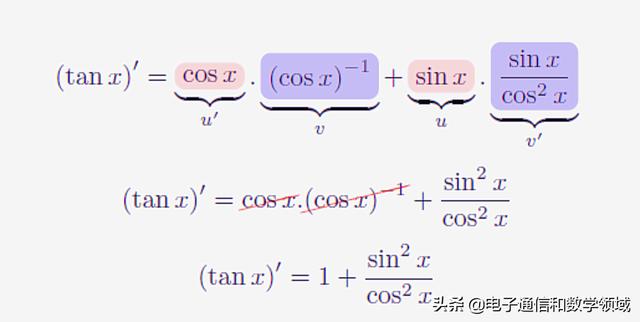
最后化简，就得到tanX导数等于(1/cosX)^2

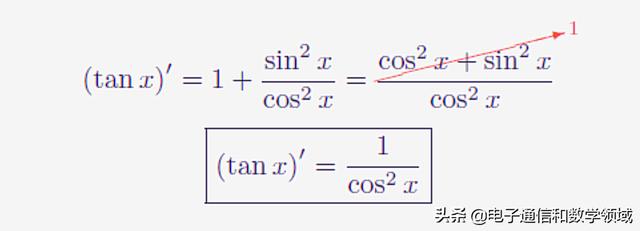
第二：几何下的推导

我们先做一个单位圆，并旋转X度时，我们可以得到用三角函数形式表示的线段，如下图所示：cosX，sinX，tanX，secX，等等。

如果把角度增加微小的量ΔX时，就得到一个微元三角形ΔABC，该三角形的面积等于1/2*Δy*1。

但ΔABC面积又等于1/2* sec(X+ΔX)* secX* sinΔX,

所以我们就得到Δy= sec(X+ΔX)* secX* sinΔX,

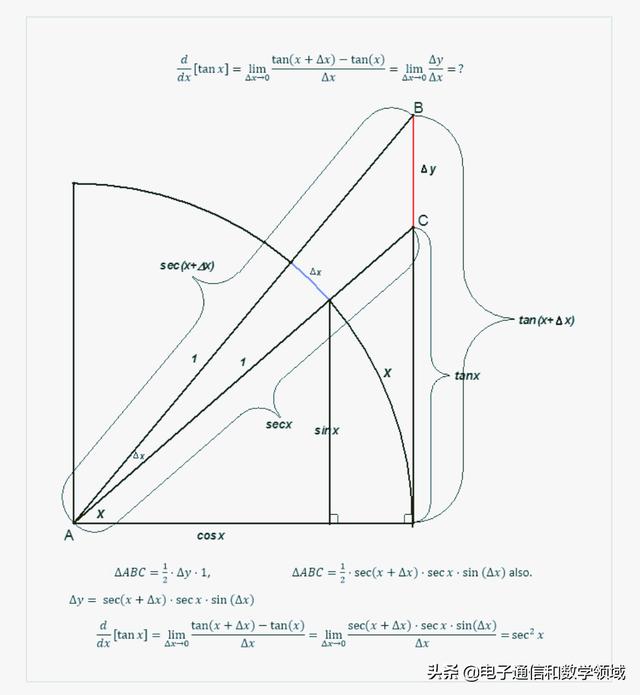
最终我们就得到了tanX的导数，它等于(1/cosX)^2，或者可以写成正割函数的平方secX^2。