三角函数π/2转化_高中数学：三角函数知识点

一、三角函数的概念

单位圆定义：设起点在原点的射线，与x轴正半轴形成一个角θ，并与单位圆(x2+y2=1)相交。这个交点的横坐标值和纵坐标值分别等于cosθ和sinθ。

单位圆定义允许三角函数对所有正数和负数辐角都有定义，而不只是对于在 0 和 π/2弧度之间的角。逆时针方向的度量是正角，而顺时针的度量是负角，对于大于2π或小于-2π的角，可继续绕单位圆旋转得到。

如：角α的终边经过点P(3,-4)，则cosα=3/5。

二、三角函数的诱导公式

任意角的三角函数均可与第一象限角的三角函数相互转化。

(奇变偶不变，符号看象限)

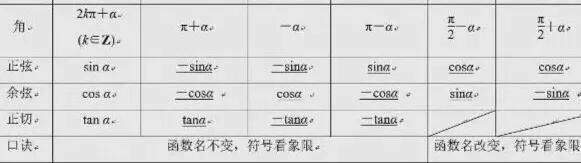
诱导公式可以概括为：对于kπ/2±α(k∈Z)的三角函数值，当k是偶数时，得到α的同名函数值，即函数名不改变；当k是奇数时，得到α相应的余函数值sin→cos;cos→sin;tan→cot；cot→tan。(奇变偶不变)，然后在前面加上把α看成锐角时原函数值的符号(符号看象限)。

如：sin(-2π－α)=sin(-4·π/2－α)，k=-4为偶数，所以取sin；α看成锐角时，-2π