节点电压法经典例题带解析_一次函数必考题（面积之铅垂法）

铅垂法：常用初中数学函数与几何综合题中，一次函数、反比例函数、二次函数求面积问题必考点，你若掌握，必是高分！(特别是平时速度不够的同学一定要仔细研磨)

题目：在平面直角坐标系中，已知A(1,1)、B(7,3)、C(4,7)，求△ABC的面积．

法1、(补——加减法)

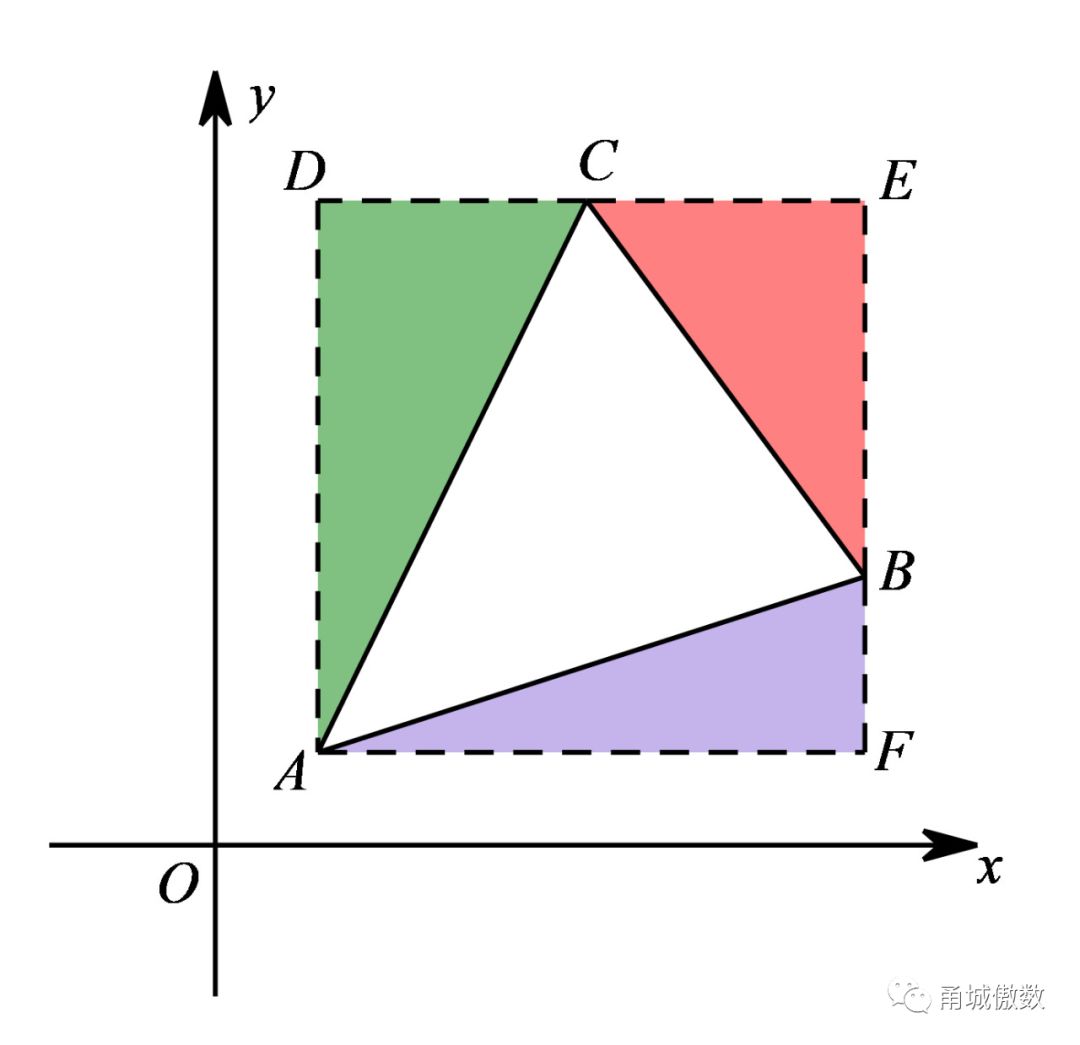
法2、(割)

可得：AE=BF=3

△AED≌△BFD     

法3、(铅垂法)

【解题步骤】

(1)求A、B两点水平距离，即水平宽；

(2)过点C作x轴垂线与AB交于点D，可得点D横坐标同点C；

(3)求直线AB解析式并代入点D横坐标，得点D纵坐标；

(4)根据C、D坐标求得铅垂高；

(5)利用公式求得三角形面积．

根据A、B两点坐标求得直线AB解析式为：

由点C坐标(4,7)可得D点横坐标为4，

将4代入直线AB解析式得D点纵坐标为2，

故D点坐标为(4,2)，CD=5,  

经典例题：(难度层层递进，强化方法吸收)

例1、如图，在平面直角坐标系中，已知A(-1，3)，B(3，-2)，则△AOB的面积为___________．

例2、如图，直线y=-x+4与x轴、y轴分别交于点A，点B，点P的坐标为(-2，2)，则S_△PAB =___________．

例3、如图，直线 y=½ x+1经过点A(1，m)，B(4，n)，点C的坐标为(2，5)，求△ABC的面积．

例4、如图，直线AB：y=x+1与x轴、y轴分别交于点A，点B，直线CD：y=kx-2与x轴、y轴分别交于点C，点D，直线AB与直线CD交于点P．若S_△APD =4.5，则k=__________．

例5、如图，在平面直角坐标系中，已知A(2，4)，B(6，6)，C(8，2)，求四边形OABC的面积．

例6、如图，直线 y=½ x-1与x轴、y轴分别交于A，B两点，C(1，2)，坐标轴上是否存在点P，使S_△ABP =S_△ABC ？若存在，求出点P的坐标；若不存在，请说明理由．

需要解析的同学可以加微信哦

努力不分背景，每个人都在奋斗，都有自己奋斗的目标和方式，之所以会拉开差距，是因为每个人奋斗的力度不同！世间最可怕的事，就是比你优秀的人比你更努力，更勤奋、更极致！