初值问题的有限差分格式实现——《MATLAB微分方程高效解法》（一）

1.序

使用MATLAB求解微分方程，算是一项基本功。坦白讲，我的基本功并不扎实。在看了《MATLAB微分方程高效解法——谱方法原理与实现》后，我想系统性的学习，并把成果学习成果形成笔记。
本文致力于实现相应算法，先简明扼要叙述数学原理，再用算例讲述MATLAB实现。

2.常微分方程初值问题

常微分方程初值问题可用下式来表示：

所谓有限差分法，也就是对变量在区间内进行离散化，然后构造递推公式，步进式地得到待求量在这些位置的近似值。最基础的递推公式是欧拉法（二步欧拉法），分为显式格式和隐式格式。在此基础上有改进的欧拉法（预测—校正法），龙格—库塔法（Runge-Kutta）。

2.1差分格式

初值已知，将导数近似为差商，有

（h即变量x的间距）
相应有
，近似认为
『显式二步欧拉格式』
也就是用f在这一点的值视为这一段区间上的平均值。直观点说，就是用这一点的切线，“以直代曲”，近似代替这一段上的曲线。或者认为是用初始点的速度来代替平均速度求路程。这种近似一定会产生误差，但只要f在这一小段上的变化不大，误差就可以接受。
这里的误差称为局部截断误差，可以用泰勒展开的形式来分析。
（泰勒展开在离散科学和工科中应用广泛，用这个框架分析，更接近本质，也更简洁优美。数学为什么在理工科中处于核心地位，就是因为它的简洁优美，直达本质。当然，仅仅是数学模型，你永远不可能学好对应的科学，你还需要对每一项的物理含义有深刻的认识）

大O表示同一量级的量。二步欧拉法的阶段误差是间距h的两次方量级，因此具有一阶精度。
既然可以用f在左端点的值近似代替，那么相应也可以用右端点，也就是隐式的欧拉法（向后差分）。由于右端点的导数不可知，方程本身不可以只把一个未知数放在一侧，所以称为隐式格式。
『隐式二步欧拉格式』
事实上，这两种欧拉法又分别被称为向前差分、向后差分。此外，还有中心差分。中心差分具有二阶精度，但需要在中点定义，离散上较繁琐，在差分法中用的不多。
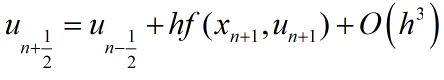『中心差分格式』
类比数值积分的方法，采用梯形法，要比只采用一端的端点值精度更高，也就是左右端点值简单取个平均。因此，有改进的欧拉法。
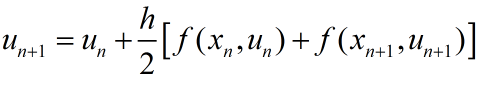『改进的欧拉法格式』
这种格式其实也是隐形的，精度是二阶。为了计算方法，先用显式欧拉法得到预测值，然后再带入上式进行修正，得到精度更高的结果。这个过程称为改进的欧拉法。
顺着改进欧拉法的思路，采用f在更多位置的线性组合，可以得到更高精度，这就是龙格—库塔法（Runge—Kutta method)。
递推公式有：

其中，Ri,ai,bij为已知系数，取不同的值，可以得到相同精度的不同格式。常用的有标准四阶龙格-库塔公式和吉尔公式。

2.2算例

MATLAB的ode系列函数，专门用来求解这一类问题，调用格式为

[X,U] = odesolver(odefun,xspan,u0,options)

MATLAB自带的常微分方程函数(odesolver)有多种，如图所示：

函数	处理问题类型	精度	描述
ode45	非刚性	中	大多数情况下的首选
ode23	非刚性	低	处理对精度要求不高或者中等刚度的问题
ode113	非刚性	低中高	处理某些问题比ode45更精确更高效
ode15s	刚性	低中	ode45失效的时候优先尝试
ode23s	刚性	低	处理对精度要求不高的刚性问题
ode23t	中等刚性	低	处理中等刚性问题
ode23tb	刚性	低	处理对精度要求不高的刚性问题

常微分方程组（odefun）可以采用句柄函数，也可以另外采用一个函数定义。
有两点额外说明：

1. 上面讲述的是一次常微分方程，也可以用来求解高阶常微分方程，只需要变量替换，得到常微分方程组。然后求解常微分方程组即可。
2. 方程有刚性非刚性之分，针对不同类型选取不同求解函数（odesolver）

一个例子：
常用的阻尼振动方程为例：

变量替换，有

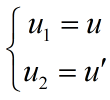
则有

接下来代码求解如下：

clear all; close all;
beta=1;omega=10;xspan=[0 5];
[x,usol]=ode45('damp',xspan,[1 0],[],beta,omega);
plot(x,usol(:,1),'k','LineWindth',1.5)
xlabel x,ylabel u
%% damp函数定义为
function du=damp(t,u,dummy,beta,omega)
du=[u(2);-2*omegau*u(2)-omega^2*u(1)];

得到图像如图：

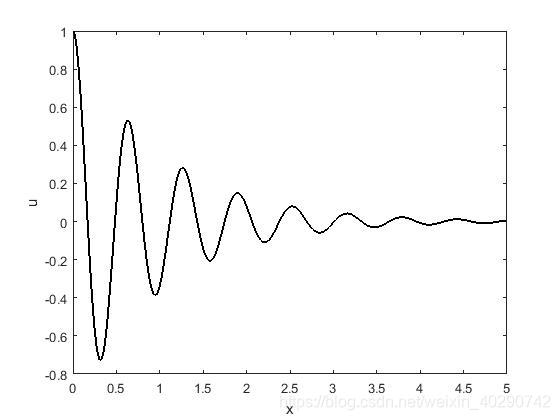
总之，可以采用上述方式得到 常微分方程初值问题的求解。

3.偏微分方程边值问题

上述代码用于求解初值问题，那么边值问题如何求解呢？
写出通用的边值问题

3.1打靶法

一种方法是近似迭代求解，也就是“打靶法”。仍采用初值问题的函数，但是由于初值不是完全可知的，需要先假定一个初值，迭代求解后得到了数值结果。
思路如下：

1. 随意选取m的起始值。
2. 求出初值问题的解
3. 若不符合，则修正m的值。
4. 重复前面两项，直到符合，此时的就是数值解。

一个例子

采用变量替换，有

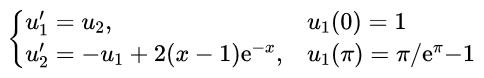
程序代码为：

clear all; close all;
x=linespace(0,pi,20);
solinit=bvpinit(x,[2 2]);
%bvp4c求解边值问题
sol=bvp4c(@shoot2,@bc,solinit);
%从结构体sol中获取指定位置的数值结果
u=deval(sol,x);
%解析解
u_exact=cos(x)+x.*exp(-x);
%画图
plot(x,u(1,:),'+k",x,u_exact,'k','MarkerSize',10,'LineWidth',1.5)
set(gca,'Fontsize',16),xlabel a,ylabel u
legend('bvp4c','解析解',0),axis([0 pi -1 1.5])

%shoot2代码
function res=bc(ua,ub)
%边界条件
res=[ua(1)-1;ub(1)+1-pi/exp(pi)];
end