椭圆曲线公钥密码体制
1 背景介绍
1.1 密码体制的含义
密码体制分为对称密码体制和非对称密码体制,非对称密码体制(公钥密码体制)是指在加密过程中,密钥被分为一对,这对密钥中的任何一个密钥都可以作为公开密钥通过非保密方式向他人公开,而另一把作为私有密钥加以保存,这密钥具有这样的特点:当知道密钥对中的一个密钥时,要检测出另一个密钥,在计算上是不可能的,公开密钥用来对信息进行加密,则私有密钥用来对信息进行解密,反之依然,在这个系统中,每一个通信实体都有一个加密密钥和一个紧密相关的解密密钥,通信的双方只要知道对方的公钥,就可以进行安全的通信。以下是一些常用的公钥密码体制
表1 3种常用公钥密钥体制
1.2 椭圆曲线密码体制
椭圆曲线在代数学和几何学上已研究了150多年,有丰富而深厚的理论积累。而椭圆曲线密码体制,即基于椭圆曲线离散对数问题的各种公钥密码体制,最早由Miller 和 Koblitz 于1985年分别独立地提出,它是利用优先于上椭圆曲线的有限点群代替基于Lisa对数问题密码体制中的有限循环群所得到的一类密码体制,对于椭圆曲线密码系统(ECC)的安全性,其数学基础是计算椭圆曲线离散对数问题(ECDLP)的难解性,一般来说,ECC没有亚指数共计,所以它的密钥长度大大地减少,256bit的ECC密码体制成为目前已知公钥密码体制中每位提供加密强度最高的一种体制。
2 算法过程
2.1 理论基础
1. 黎曼几何中的“平行线”
欧几里得《几何原本》中的第五条公设:两直线被第三条直线所截,如果同侧两内角和小于两个直角, 则两直线作会在该侧相交(平行公设)。
《几何原本》中只有第29条命题,一条直线与两条平行直线相交,则所成的内错角相等,同位角相等,且同旁内角之和等于两直角,才用到了第五公设,其他命题并没有使用到,因此一些数学家提出疑问:第五公设能否不作为公设,而作为一条定理?能否靠前四条公设证明之?因此出现了长期的关于“平行线理论”的讨论。
欧氏几何讲“过直线外一点有且只有一条直线与已知直线平行”,后面就有个罗氏几何(罗巴切夫斯基)讲“过直线外一点至少存在两条直线和已知直线平行”,那么是否有“过直线外一点,不能做直线和已知直线平行?”,黎曼几何就回答了这个问题。
黎曼几何中不承认平行线的存在,即在同一平面内任何两条直线都有公共点(交点)。另一条公设讲:直线可以无限延长,但总的长度是有限的。
黎曼几何也被称为椭圆几何。椭圆曲线就是基于黎曼几何的“平行线理论”。
2. 无穷远点
定义平行线相较于无穷远点P∞,使平面上所有直线都有唯一的交点。
无穷远点的性质:
• 一条直线只有一个无穷远点。
• 平面上一组相互平行的两条直线有公共的无穷远点。
• 平面上任何相交的直线有不同的无穷远点(否则就会存在两个交点)。
• 平面上全体无穷远点构成一条无穷远直线。
• 平面上全体无穷远点与全体平常点构成射影平面。

图1 两条平行直线相较于无穷远点
3. 射影平面坐标系
射影平面坐标系是对笛卡尔平面直角坐标系的扩展。普通平面直角坐标系无法表示无穷远点,因此为了表示无穷远点的坐标,产生了射影平面坐标系
射影平面点的表示:
点:对普通平面直角坐标系上的点A(x,y),令x=X/Z,y=Y/Z(Z≠0),则点A在射影平面上表示为(X:Y:Z)
那么对于平面直角做标记上的点(1,2),1= X/Z,2= Y/Z,则在射影平面上坐标为(Z:2Z:Z)Z≠0,所以A(1,2,1),B(2,4,2),C(3,6,3)……等表示形式为(Z:2Z:Z)的点都是A点在新坐标系中的坐标表示。
线:无穷远直线表达式对应 Z= 0
证明:
空间直角坐标系中,直线方程为:Ax + By +C = 0 (AB不同时为0),
射影坐标系中: A(X/Z) + B(Y/Z) + C = 0,
左右乘以Z可以得到新的直线方程为: AX+ BY + CZ = 0
现在假设有两条平行线:
L1: AX + BY + C1Z = 0
L2: AX + BY + C2Z = 0
C1 != C2 ,根据平行线的定义(斜率相同)可以得知L1 //L2
联立两条直线方程求解可以得知:
L1 : C1Z = -( AX + BY)
L2 : C2Z = -( AX + BY)
∴C1Z = C2Z =-( AX + BY)
∵C1 != C2
∴ Z = 0
∴-( AX + BY)= 0,即(AX + BY=0)
∴表达式为:AX + BY + C*0 = 0
得证:无穷远直线表达式对应 Z= 0
无穷远点的坐标表示:
L1 : X + 2Y +3Z =0
L2: X + 2Y + Z = 0
由系数可知L1 // L2 ,按照黎曼几何的平行线理论,两条线交于无穷远点
由上面的证明可知X = -2Y
代入坐标点表示的话就是:
(注意无穷点处Z=0)
(-2Y:Y:0)
所以(-2:1:0)(-4:2:0)等形如(-2Y:Y:0) 在Y !=0时 的坐标表示就可以表示无穷点。
4. 椭圆曲线方程
把椭圆曲线放到平面直角坐标系:求出平面直角坐标系上椭圆曲线所有平常点组成的曲线方程,再加上无穷远点,就构成了椭圆曲线。
椭圆曲线方程是建立在射影平面坐标系下的满足一齐次方程——威尔斯特拉斯方程:

对普通平面上点(x,y),令x=X/Z,y=Y/Z,Z≠0,得到如下方程:

约掉一个Z^3得到普通平面坐标系
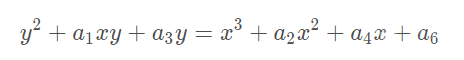
注意:
(1) 椭圆曲线方程是一个齐次方程,与椭圆没有关系,是由椭圆曲线的描述方程类似于计算椭圆周长的方程,转化为积分 ,分母的函数项 两边平方即可得到椭圆曲线方程
(2) 曲线上的每个点都必须是非奇异的(光滑的),所谓非奇异,是指曲线上任意一点的偏导数Fx(x,y,z),Fy(x,y,z),Fz(x,z,y)不能同时为0。简单来说就是满足方程的任意一个点都存在切线。(保证所有数都有逆元)
举例:
一个比较经典的椭圆曲线:
y^2 = x^3 -x

图2 椭圆曲线
5. 群的概念
群:
群是一种代数结构,由一个集合以及一个二元运算组成,已知集合和运算(G,)如果是群则必须满足如下要求:
a. 封闭性:∀a,b∈G,ab ∈ G
b. 结合性: ∀a,b,c∈G ,有 (ab)c = a (bc)
c. 单位元:ョe∈G, ∀a ∈G,有ea = ae = a
d. 可逆:∀a ∈G ,ョb∈G 使得 ab = ba = e
阿贝尔群:
阿贝尔群的话还需要满足交换性: a b = b a
比如在整数内的加法运算就是一个阿贝尔群(Z,+)
a. 封闭性满足:a和b都 ∈ Z 那么 a+b一定也∈Z
b. 结合性满足:(a+b) + c = a+ (b +c )
c. 单位元满足: 0即为单位元,因为所有整数来说 a+0=0+a=a
d. 逆向满足:a的逆元为-a 因为a+(-a) = 0 就是单位元
所以整数Z的加法运算(Z,+)属于阿贝尔群
6. 椭圆曲线上的阿贝尔群
椭圆上的群操作:假设用加法符号“+”表示,给定两个点及其坐标,P(x1,y1),Q(x2,y2),计算第三个点R坐标:
以上面作图的椭圆曲线为例:
y^2 = x^3 -x
在曲线上找一个点P和Q,过P和Q作一条直线,交椭圆曲线为点R’,再过R’点 作垂直于x轴的直线,交曲线另一点为R。定义P+Q = R如下图所示:

图3 相异点做加法
当P=Q的时候,则过P点的切线相交与椭圆曲线为R’,作x轴的垂直线相交与R

图4 P, Q两点异同的对比图
左图 R=P+Q, 右图:R=P+P=2P
例子: R=3P时
在右边图这种情况的时候,P=Q,我们已经得到了R=P+P,那么现在连接R和P作一条新的直线与曲线相交于R2,那么R2 = R+P,也就是R2 = P+P+P
往复循环,R3 = P+P+P+P

图5 求3P的作图
引入无穷远点O∞构造阿贝尔群
要想构造阿贝尔群,还需要引入一个无穷远点O∞充当0元,现在假设椭圆曲线无穷远点O∞与椭圆曲线上一个点P的连线交于了P’,过P’作y轴的平行线相交与P,所以有无穷远点O∞ + P = P,这样无穷远点的O∞的作用于普通加法中0的作用相同。所以无穷点远O∞也被成为零元,P’成为P的负元,简称负P

图6 P与-P在一条垂直线上
根据上面的描述又可以得知:如果椭圆曲线上三个点P1 P2 P3在同一条直线上的话,那么他们的和等于零元。也就是P1 + P2 + P3 = O∞(即P1 + P2=P3‘)
构成阿贝尔群
封闭性:两个椭圆上的点加和还在椭圆上
交换律:两个椭圆上的点相加可以改变先后顺序
结合性:三个椭圆上的点想加可以(A+B)+C=A+(B+C)
单位元:无穷远点O∞ ,O∞+ P = P
逆元:关于X轴对称的另一边的点P’,P+P’= O∞
7. 有限域上的椭圆曲线
实数域上的椭圆曲线是连续的,并不适用于加密,考虑到加密算法的可实现性,要把椭圆曲线定义在有限域上,使之变成离散的点。
给定一个有限域Fp:
• Fp只有p(p为素数)个元素0,1,2…p-2,p-1;
• Fp的加法(a+b)法则是a+b≡c(mod p);
• Fp的乘法(a×b)法则是a×b≡c(mod p);
• Fp的除法(a÷b)法则是a÷b≡c(mod p),即a×b^-1≡c(mod p),b^-1为b的逆元;
• Fp的单位元是1,零元是0;
• Fp域内运算满足交换律、结合律、分配律。
8. 适合加密的椭圆曲线方程:
并非所有的椭圆曲线都适合加密。下面定义一类适合加密的椭圆曲线:
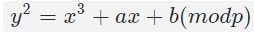
椭圆曲线Ep(a,b),p为质数,x,y∈[0,p-1]:
选择两个满足下列约束条件的小于p的非负整数a、b:
Δ=-16(4a3 + 27b2) mod p ≠ 0 (保证曲线是光滑的,即曲线的所有点都没有两个或者两个以上的不同的切线。)
• 无穷远点O∞是零元,有O∞+O∞=O∞,O∞+P=P;
• P(x,y)的负元是(x,-y),有P+(-P)=O∞;
• P(x1,y1),Q(x2,y2)和R(x3,y3)有如下关系:
x3≡k2-x1-x2(mod p) y3≡k(x1-x3)-y1(mod p)
• 其中若P=Q则
k=(3x2+a)/2y1mod p
若P≠Q则
k=(y2-y1)/(x2-x1) mod p
k为直线斜率。
证明:

9. 有限域椭圆曲线点的阶:
如果椭圆曲线上一点P,存在最小的正整数n使得数乘nP=O∞,则称n为P的阶,若n不存在,则P为无限阶。
在有限域上定义的椭圆曲线,所有点的阶n都是存在的。
2.2 基于离散对数上的难解问题
等式Q=dG(Q,G为Ep(a,b)上的点,d为小于n(n是点G的阶)的整数),在有限域上的椭圆曲线,给定d和G,根据有限域上的加法法则,很容易计算出Q;但给定Q和G,很难计算出d,因为只能遍历每一个x做运算。这就是椭圆曲线的离散对数难题。
点G称为基点,d为私钥,Q为公钥。
举例:
以椭圆曲线上的点P =(3,10)为基点,按照椭圆曲线“加法”运算的规则计算2P,3P,4P…结果如下图所示

图7 2P,3P,4P…
所产生的点可以说是无规律可言,例如点P = (3,10),点23P = (9,7)。在这里求离散对数问题就相当于已知点(3,10)和点(9,7),求23。在这个例子中p=23,问题还不难解,如果当p数值非常大时,要求出这个解是十分困难的。
2.3 加解密过程
1、加解密过程
- 选定一条椭圆曲线 Ep(a,b) 并取椭圆曲线上一点,作为基点P。
- 选择一个大数k作为私钥,并生成公钥 Q=kP。
- 将 Ep(a,b) 和点Q、P传给用户。
- 用户接到信息后 ,将待传输的明文编码到Ep(a,b)上的一点M,并产生一个随机整数r。
- 公钥加密(密文C是一个点对):
C={C1,C2}{rP, M+rQ} - 私钥解密(M + rQ - k(rP) ,解密结果就是点M),公式如下:
C2-kC1=M + rQ - k(rP) = M + r(kP) - k(rP) = M
7、对点M进行解码就可以得到明文
假设在加密过程中,有一个第三者H,H只能知道椭圆曲线 Ep(a,b)、公钥Q、基点P、密文点C,而通过公钥Q、基点P求私钥k或者通过密文点C、基点P求随机数r都是非常困难的,因此得以保证数据传输的安全。
2.4 攻击
对于公钥密码体制的安全性要求一般都是针对密文的特性而言的,就是说,密文应该满足某种安全特性。目前被国际密码界广泛接受的密文的安全性要求主要有以下几种:单向性,不可区分性和不可扩展性。
单向性就是说攻击者在没有拥有私钥的前提下,无法计算出任何密文m所对应的明文信息m.
不可区分性就是说对己知给定的两个明文,加密者随机一致的选择其中一个进行加密,攻击者无法从密文中知道是对哪个明文的加密。
不可扩展性就是说攻击者无法构造与已给密文相关的新密文。
在公钥密码体制中,攻击者拥有公钥,他可以随便选择明文进行加密,攻击者还有机会获得密文,而且还可能利用各种途径来获得解密,为此,公钥密码体制应该不会泄露其他密文的明文信息,这就要求该密码体制能抗选择密文攻击。
椭圆曲线密码体制的安全性基于椭圆曲线离散对数问题(ECDLP) 的难解性。目前还没有有效的快速算法来解决这一难题,它只有指数级的算法,这也是椭圆曲线密码体制的安全基础。ECDLP 问题就是,给定椭圆曲线E, 基点P和P的一个标量乘Q, 来确定一个正整数k, 满足Q=kP.从目前的研究来看,ECDLP 比有限域上离散对数问题(DLP) 更加难以处理。已经知道的对椭圆曲线的攻击方法,主要有以下几种,设椭圆曲线上得几点,P的阶为n
1, 穷举搜索法
计算2P, 3P, 4P, ···直到找到Q, 这种算法最多需要n步椭圆曲线的点加。
2. 大步小步法
这种算法的思想在于测试P的倍点运算是否等于Q, 利用一种数据结构,具体的做法是,预先计算并存储一些P的某些倍点(小步)运算的结果,然后对于某个整数I, 计算Q-IP, Q-21P, ··. (大步), 直到@-iIP在预存表中出现。
3. MOV 攻击
其核心思想是将椭圆曲线离散对数问题转化为某个有限域的乘法群上的离散对数问题,此类攻击只对超奇异椭圆曲线有效。该算法导致出现了亚指数的
ECDLP 求解算法,所以在对椭圆曲线的参数进行选择的时候,避免出现这一情况的出现。
4. Weil descent 攻击
这种方法只适合于特征值为2的复合域,在椭圆曲线密码体制的实际应用中,们可以选择m为素数的GF (2”) 来避免此类攻击。
5. Pollard’s rho 算法
从目前来看,对ECDLP最有效的攻击就是并行 Pollard’s rho 算法攻击,这种算法是小步大步算法的随机版本,它的运行时间和小步大步算法差不多,只是需要很小的存储空间,该算法可以在几种处理器上并行,其运行时间为✓元m步点加运算。
有学者指出,如果m~2120, 花费 1000万美元建立具有325000 并行处理的Pollard’s rho 算法来解决 ECDLP 需要32天左右,而在实际的工作中,我们一般采用的都是m≥160, 因此可以说椭圆曲线密码体制是比较安全的,
Certicom是ECC的主要商业支持者,拥有超过130项专利,并且已经以2500万美元的交易获得了国家安全机构(NSA) 的技术许可。他们也已经发起了许多对ECC 算法的挑战。已经被解决的最复杂的是109位的密钥,是在2003年初由一个研究团队破解的。破解密钥的这个团队使用了基于生日攻击的大块并行攻击用超过10, 000 台奔腾级的 PC 机连续运行了540天以上。对于ECC推荐的最小密钥长度163位来说,当前估计需要的计算资源是109位问题108倍。
3 算法实现
3.1 运行环境
python3.7
3.2 明文:
125个大写字母,共1000bit
ABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTU
3.3 实验结果
1、参数p设为11,耗时34s



2、参数p设为2011,耗时78s


3.4 结果分析
密码学中,描述一条Fp上的椭圆曲线,常用到六个参量: T=(p,a,b,P,n,h)。 (p 、a 、b 用来确定一条椭圆曲线,P为基点,n为点G的阶,h 是椭圆曲线上所有点的个数m与n相除的整数部分)这几个参量取值的选择,直接影响了加密的安全性。参量值一般要求满足以下几个条件:
1、p 当然越大越安全,但越大,计算速度会变慢,200位左右可以满足一般安全要求;
2、p≠n×h;
3、pt≠1 (mod n),1≤t<20;
4、4a3+27b2≠0 (mod p);
5、n 为素数;
6、每次随机选取的数字r要小于P的阶数
7、h<=4
4 总结及分析
1、总结
ECC加密算法是一种公钥加密技术,以椭圆曲线理论为基础。利用有限域上椭圆曲线的点构成的Abel群离散对数难解性,实现加密、解密和数字签名。将椭圆曲线中的加法运算与离散对数中的模乘运算相对应,就可以建立基于椭圆曲线的对应密码体制。
由前面可以看出,ECC算法的数学理论非常深奥和复杂,在比较难于实现,但它的单位安全强度相对较高,它的破译或求解难度基本上是指数级的,黑客很难用通常使用的暴力破解的方法来破解。RSA算法的特点之一是数学原理相对简单,在工程应用中比较易于实现,但它的单位安全强度相对较低。因此,ECC算法的可以用较少的计算能力提供比RSA加密算法更高的安全强度,有效地解决了“提高安全强度必须增加密钥长度”的工程实现问题。
2、分析
①加法要注意的情况:零元、坐标(x,y) y=0时的情况、逆元情况
②乘法实现一般是分解成二进制的位来计算,这样快很多…ECC暴力破解暴难度大也是在这里(目前没公开的其它捷径)
③明文编码到一个点,通常用概率编码, 代码层面要实现 勒让德符号 来计算 二次剩余。另外还要处理不能编码的小概率情况。
④关于密钥创建等,比如大质数生成,涉及到的素性校验…
5 参考文献
[1]彭林.参天大树从地起——影响深远的欧几里得《几何原本》[J].中学数学教学参考,2006(12):49-52.
[2]刘建新,曲安京.黎曼论几何学基础之假设[J].科学技术哲学研究,2018,35(05):89-93.
[3]Paul Gauduchon,Andrei Moroianu. Non-existence of orthogonal coordinates on the complex and quaternionic projective spaces[J]. Journal of Geometry and Physics,2020.
[4]王佳琪. 基于超椭圆曲线同态加密的安全访问控制算法与云计算研究[D].陕西科技大学,2019.
[5]朱玉清,庄金成,于伟,林东岱.特征p椭圆曲线上p-群的离散对数问题[J].密码学报,2018,5(04):368-375.
[6]刘芳芳,刘增芳,芦殿军.大数模幂运算与椭圆曲线标量乘运算的实现及数据仿真[J].通信技术,2019,52(06):1482-1487.
[7]孟春岩.在超椭圆曲线上实现DSA数字签名[J].软件,2019,40(03):134-136.
[8]王亚辉. RSA密码的量子攻击方法研究[D].武汉大学,2017.
js/
6 附录
# -*- coding:utf-8 -*-
def get_inverse(value, p):
"""
求逆元
:param value: 待求逆元的值
:param p: 模数
"""
for i in range(1, p):
if (i * value) % p == 1:
return i
return -1
def get_gcd(value1, value2):
"""
辗转相除法求最大公约数
:param value1:
:param value2:
"""
if value2 == 0:
return value1
else:
return get_gcd(value2, value1 % value2)
def get_PaddQ(x1, y1, x2, y2, a, p):
"""
计算P+Q
:param x1: P点横坐标
:param y1: P点纵坐标
:param x2: Q点横坐标
:param y2: Q点纵坐标
:param a: 曲线参数
:param p: 曲线模数
"""
flag = 1 # 定义符号位(+/-)
# 如果P=Q,斜率k=(3x^2+a)/2y mod p
if x1 == x2 and y1 == y2:
member = 3 * (x1 ** 2) + a # 分子
denominator = 2 * y1 # 分母
# 如果P≠Q, 斜率k=(y2-y1)/(x2-x1) mod p
else:
member = y2 - y1
denominator = x2 - x1
if member * denominator < 0:
flag = 0 # 表示负数
member = abs(member)
denominator = abs(denominator)
# 化简分子分母
gcd = get_gcd(member, denominator) # 最大公约数
member = member // gcd
denominator = denominator // gcd
# 求分母的逆元
inverse_deno = get_inverse(denominator, p)
# 求斜率
k = (member * inverse_deno)
if flag == 0:
k = -k
k = k % p
# 计算P+Q=(x3,y3)
x3 = (k ** 2 - x1 - x2) % p
y3 = (k * (x1-x3) -y1) % p
return x3, y3
def get_order(x0, y0, a, b, p):
"""
计算椭圆曲线的阶
"""
x1 = x0 # -P的横坐标
y1 = (-1 * y0) % p # -P的纵坐标
temp_x = x0
temp_y = y0
n = 1
while True:
n += 1
# 累加P,得到n*P=0∞
xp, yp = get_PaddQ(temp_x, temp_y, x0, y0, a, p)
# 如果(xp,yp)==-P,即(xp,yp)+P=0∞,此时n+1为阶数
if xp == x1 and yp == y1:
return n+1
temp_x = xp
temp_y = yp
def get_dot(x0, a, b, p):
"""
计算P(x0,y0)和-P(x1,y1)
"""
y0 = -1
for i in range(p):
# 满足适合加密的椭圆曲线条件,Ep(a,b),p为质数,x,y∈[0,p-1]
# (y^2)mod p ≡ (x^3+ax+b)mod p
if i**2 % p == (x0**3 + a*x0 + b) % p:
y0 = i
break
# 如果找不到合适的y0返回False
if y0 == -1:
return False
# 计算-y
x1 = x0
y1 = (-1*y0) % p
return x0, y0, x1, y1
def get_graph(a, b, p):
"""
画出椭圆曲线散点图
"""
xy = []
# 初始化二维数组
for i in range(p):
xy.append(['-' for i in range(p)])
for i in range(p):
value = get_dot(i, a, b, p)
if (value != False):
x0,y0,x1,y1 = value
xy[x0][y0] = 1
xy[x1][y1] = 1
print('椭圆曲线散点图:')
for i in range(p):
temp = p - 1 -i
if temp >= 10:
print(temp, end='')
else:
print(temp, end='')
# 输出具体坐标值
for j in range(p):
print(xy[j][temp], end='')
print()
print(' ', end='')
for i in range(p):
if i >= 10:
print(i, end='')
else:
print(i, end='')
print()
def get_kP(xP, yP, priv_key, a, p):
"""
计算kP(公钥)
"""
temp_x = xP
temp_y = yP
while priv_key != 1:
temp_x, temp_y = get_PaddQ(temp_x, temp_y, xP, yP, a, p)
priv_key -= 1
return temp_x, temp_y
def get_KEY():
"""
生成公钥私钥
"""
# 选择曲线方程
while True:
a = int(input('用户A:输入椭圆曲线参数a(a>0)的值:'))
b = int(input('用户A:输入椭圆曲线参数b(b>0)的值:'))
p = int(input('用户A:输入椭圆曲线参数p(p为素数)的值:'))
# 满足曲线判别式(4a^3 + 27b^2) mod p ≠ 0
if (4*(a**3)+27*(b**2))%p == 0:
print('输入的参数有误,请重新输入!\n')
else:
break
# 输出曲线散点图
get_graph(a, b, p)
# 选择基点P
print('用户A:在上图坐标系中选择基点P的坐标')
Px = int(input('横坐标Px:'))
Py = int(input('纵坐标Py:'))
# 获取曲线的阶
n = get_order(Px, Py, a, b, p)
# 生成私钥k,且k<n
priv_key = int(input("用户A:请输入私钥k(<{}):".format(n)))
#生成公钥Q
Qx, Qy = get_kP(Px, Py, priv_key, a, p)
print("公钥Q({},{})".format(Qx,Qy), end="\n")
return Qx, Qy, priv_key, a, b, p, n, Px, Py
def encrypt(Px, Py, Qx, Qy,priv_key, a, p, n):
"""
加密,通过明文字符的ASCII码乘点kQ的x坐标得到,即incharkQx
"""
r = int(input('用户B:输入一个随机整数r(<%d)用于计算rP和rQ:' .format(n)))
rPx, rPy = get_kP(Px, Py, r, a, p) # rG
rQx, rQy = get_kP(Qx, Qy, r, a, p) # rQ
print("密文c1({},{})".format(rPx, rPy), end="\n")
print("密文c2的kQ({},{})".format(rQx, rQy), end="\n")
plain = input('用户B:输入需要加密的字符串:')
plain = plain.strip()
c = []
print('密文为:', end='')
for char in plain:
intchar = ord(char)
cipher = intchar * rQx
c.append([rPx, rPy, cipher])
print('(%d,%d),%d' % (rPx, rPy, cipher), end=' ')
print()
return c
def decrypt(c, priv_key, a, p):
"""
解密
"""
for charArr in c:
decrypto_text_x,decrypto_text_y = get_kP(charArr[0], charArr[1], priv_key, a, p)
print(chr(charArr[2] //decrypto_text_x), end='')
print()
if __name__ == '__main__':
Qx, Qy, priv_key, a, b, p, n, Px, Py = get_KEY()
c = encrypt(Px, Py, Qx, Qy, priv_key, a, p, n)
decrypt(c, priv_key, a, p)
























 3121
3121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








