HMM总结

概率图模型
code

4.HMM–>CRF

4.1 HMM–是个序列

• x-观测到的
• 条件独立
  • 给定yt
    • $y_{t-1}和y_{t+1}(所有的过去和未来也都独立）$独立
    • $x_u和x_s$独立
• 表示
  • 状态分布：${\pi }_i=p(y_1^i=1)$
  • 状态转移矩阵A，aij为转移概率
    • $P(y_{t+1}^j|y_t^i=1)$
  • 发射概率$P(x|y)$
  • 则联合概率$P(x,y)=p(y_1){\Pi }_{t=1}^{T-1}P(y_{t+1}^j|y_t^i){\Pi }_{t=1}^{T}P(x_t|y_t)$
    • 参数化$P(x,y)={\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t)$
• 三个基础问题
  1. 状态序列解码（推断）问题：
     • 给定$x,\theta -->y:p(y|x,\theta )$
  2. 似然评估问题evaluate
     • 给定$x,\theta -->似然函数P(x|\theta )$
  3. 参数估计问题(学习
     • 给定$x-->\theta =argmaxP(x|\theta )$

4.1.1 推断问题（evaluate）

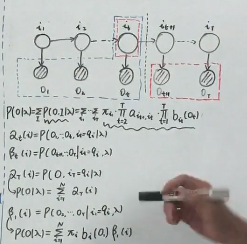
• $$\begin{gathered} P(x)={\Sigma }_{y_1,y_2,...,y_T}P(x,y)={\Sigma }_{y_1,y_2,...,y_T}{\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t) \\ ={\Sigma }_{y}P(x|y)p(y) \\ ={\Sigma }_{y_1}{\Sigma }_{y_2}...{\Sigma }_{y_T}{\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t) \end{gathered}$$
  • y i = { q 1 , q 2 , . . . , q N } − − − O ( N T ) 太 y_i=\{q_1,q_2,...,q_N\}---O(N^T)太 yi​={q1​,q2​,...,qN​}−−−O(NT)太
  • 很多连乘，但是并不是跟所有的都有关，就可以往后推求和
• $P(y_t|x)=\frac{P(x|y_t)P(y_t)}{P(x)}=\frac{P(x1,...,x_t|y_t)P(x_{t+1},...,x_n|y_t)P(y_t)}{P(x)}$
  • $P(y_t|x)=\gamma (y_t)=\frac{P(x1,...,x_t,y_t)P(x_{t+1},...,x_n|y_t)}{P(x)}=\frac{\alpha (y_t)\beta (y_t)}{P(x)}$
    • $p(x)={\Sigma }_{y_t}\alpha (y_t)\beta (y_t)$
    • 其中𝛼(𝑦𝑡)是产生部分输出序列 𝑥1, ⋯ , 𝑥𝑡并结束于𝑦𝑡的概率
    • 其中β(𝑦𝑡)是从𝑦𝑡状态开始产生输出序列𝑥𝑡+1, ⋯ , 𝑥𝑇的概率
• 递归的计算
  • $\alpha (y_{t+1})={\Sigma }_{y_t}\alpha (y_t)a_{y_{t+1},y_t}P(x_{t+1}|y_{t+1})$
    • 初始化$\alpha (y_0)=P(x_0,y_0)=p(x_0|y_0)P(y_0)=P(x_0|y_0){\pi }_{y_0}$
  • $\beta (y_t)={\Sigma }_{y_{t+1}}\beta (y_{t+1})a_{y_{t+1},y_t}P(x_{t+1}|y_{t+1})$
    • 初始化$\beta (y_T)=1就行了$
      • $假定\beta (y_T)为单位向量，我们可以准确计算出{\beta }_{y_{T-1}}$
        • $P(x)={\Sigma }_i\alpha (y_T^i)\beta (y_T^i)={\Sigma }_i\alpha (y_T^i)=P(x)$
  • 为了计算所有的yt的后验概率，需要为每一步计算alpha/beta—一次前向一次后向
  • $$\begin{gathered} \xi (y_t,y_{t+1})=P(y_t,y_{t+1}|x) \\ =\frac{P(x|y_t,y_{t+1})P(y_{t+1}|y_t)P(y_t)}{p(x)} \\ =\frac{P(x1,...x_t|y_t)P(x_{t+1}|y_{t+1})P(x_{t+2},...x_n|y_{t+1})P(y_{t+1}|y_t)P(y_t)}{p(x)} \\ =\frac{\alpha (y_t)P(x_{t+1}|y_{t+1})\beta (y_{t+1})a_{y_{t+1},y_t}}{p(x)} \end{gathered}$$
  • 似然函数–简单求和最终步的$\alpha$可得到
  • 状态的后验概率–$再使用\beta 递归$
  • –>$P(y_t^k=1|x)=\frac{\alpha (y_t)\beta (y_t)}{P(x)}$
  • –>如何得到整个序列的最大后验证概率

4.1.2 viterbi decoding解码

• $y\ast =argma{x}_{y}P(y|x)=argma{x}_{y}P(x,y)$
• $V_t^k=ma{x}_{y_1,...,y_{t-1}}P(x_1,...,x_{t-1},y_1,...,y_{t-1},x_t,y_t^k=1)$
  • 结尾为$y_t=k$时，最可能状态序列的概率
  • 递归形式$$\begin{gathered} V_t^k=p(x_t|y_t^k=1)ma{x}_i{V}_{t-1}^i{a}_{i,k} \\ {a}_{i,k}=p(y_{i}k|y_i):i->k \end{gathered}$$
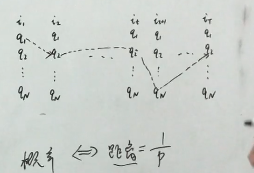
  • 动态规划（路径规划）问题：距离=1/p，使得cost最小
  • $$\begin{gathered} V_t^k：t时刻，y_t=k--到达q_k状态 \\ ma{x}_{y_1,...,y_{t-1}}终点已经确定，路径没有确定，找概率最大的路径 \end{gathered}$$
    

4.1.3 学习，参数估计

• 极大似然估计：EM算法

  • 最大化$P(x|\theta )$
  • 参数$A、\pi ,输出分布的参数$

• $P(x|\theta )={\Sigma }_{y_1,y_2,...,y_T}P(x,y)={\Sigma }_{y_1,y_2,...,y_T}{\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t,\eta )$

• $假设P(x_t|y_t,\eta )={\Pi }_{i=1}^M{\Pi }_{j=1}^L[{\eta }_{ij}{]}^{y_t^i{x}_t^j}$

• M
  

• $$\begin{gathered} {\hat{\alpha }}_{ij}=\frac{m_{ij}}{{\Sigma }_{k=1}^N{m}_{ik}} \\ {\hat{\eta }}_{ij}=\frac{n_{ij}}{{\Sigma }_{k=1}^N{n}_{ik}} \\ {\hat{\pi }}_i=y_1^i \end{gathered}$$

• E步
  
  

• 缺点

  • 仅捕捉了状态之间和状态及其对应输出之间的关系（上下文）
  • 学习目标和预测目标不匹配
    • 我们只要p(y|x),但只知道p(x,y)—产生式模型

4.1.4计算实例

* A:aij:i->j

• 前向计算
  • 时间1：
    • $$\begin{gathered} \alpha (y_1=1)=P(x_1|y_1=1){\pi }_{y_1=1}=0.5\ast 0.2=0.1 \\ （x1=红）\alpha (y_1=2)=P(x_1|y_1=2){\pi }_{y_1=2}=0.4\ast 0.4=0.16\alpha (y_1=3)=P(x_1|y_1=3){\pi }_{y_1=3}=0.7\ast 0.4=0.28 \end{gathered}$$
  • 时间2:x2=白
    • $$\begin{gathered} \alpha (y_2=1)=({\Sigma }_{y_1}\alpha (y_1)P(y_2=1|y_1))P(x_2|y_2)=(0.1\ast 0.5+0.16\ast 0.3+0.28\ast 0.2)\ast 0.5=0.077 \\ \alpha (y_2=2)=(\alpha (y_1=1)P(y_2=2|y_1=1)+\alpha (y_1=2)P(y_2=2|y_1=2)+\alpha (y_1=3)P(y_2=2|y_1=3))\ast P(x_2|y_2=2)=(0.1\ast 0.2+0.16\ast 0.5+0.28\ast 0.3)\ast 0.6=0.1104 \\ \alpha (y_2=3)=(0.1\ast 0.3+0.16\ast 0.2+0.28\ast 0.5)\ast 0.3=0.0606 \end{gathered}$$
  • 时间3：x3=红
    • $$\begin{gathered} \alpha (y_3=1)=(0.077\ast 0.5+0.1104\ast 0.3+0.0606\ast 0.2)\ast 0.5=0.4187 \\ \alpha (y_3=2)=(0.077\ast 0.2+0.1104\ast 0.5+0.0606\ast 0.3)\ast 0.4=0.03551 \\ \alpha (y_3=3)=(0.077\ast 0.3+0.1104\ast 0.2+0.0606\ast 0.5)\ast 0.7=0.05284 \\ p(x)={\Sigma }_i\alpha (y_T^i)=\alpha (y_3=1)+\alpha (y_3=2)+\alpha (y_3=3)=0.13022 \end{gathered}$$
• 后向计算：
  • $\beta (y_3=1)=1，\beta (y_3=2)=1，\beta (y_3=3)=1$
  • 时间2
    • $$\begin{gathered} \beta (y_2)={\Sigma }_{y_3}\beta (y_3)a_{y_3,y_2}P(x_3|y_3) \\ =\beta (y_3=1)a_{y_3=1,y_2}P(x_3|y_3=1)+\beta (y_3=2)a_{y_3=2,y_2}P(x_3|y_3=2)+\beta (y_3=3)a_{y_3,y_2}P(x_3|y_3=3) \end{gathered}$$
    • $\beta (y_2=1)=1\ast 0.5\ast 0.5+1\ast 0.2\ast 0.4+1\ast 0.2\ast 0.7=0.47$
    • $\beta (y_2=2)=1\ast 0.3\ast 0.5+1\ast 0.5\ast 0.4+1\ast 0.2\ast 0.7=0.49$
    • $\beta (y_2=3)=1\ast 0.2\ast 0.5+1\ast 0.3\ast 0.4+1\ast 0.5\ast 0.7=0.57$
  • 时间1
    • $\beta (y_2=1)=0.47\ast 0.5\ast 0.5+0.49\ast 0.2\ast 0.6+0.57\ast 0.2\ast 0.3=0.2105$
    • $\beta (y_2=2)=0.47\ast 0.3\ast 0.5+0.49\ast 0.5\ast 0.6+0.57\ast 0.2\ast 0.3=0.2517$
    • $\beta (y_2=3)=0.47\ast 0.2\ast 0.5+0.49\ast 0.3\ast 0.6+0.57\ast 0.5\ast 0.3=0.2207$

代码

import torch
import torch.nn as nn
import torch.optim as optim
y_size=3;
x_size=2;
transition=torch.tensor([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
b=torch.tensor([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
pi=torch.tensor([[0.2],[0.4],[0.4]])
x=[0,1,0]
def alpha(x):#前向算法p(x1,x2,x3,...,xt,yt)
        alpha=(b[:,x[0]]*pi[:].reshape(y_size)).reshape(1,y_size)
        # print(alpha)
        for i in range(1,len(x)):
            alpha=torch.cat((alpha,(torch.matmul(alpha[i-1],transition)*b[:,x[i]]).reshape(1,y_size)),0)
        return alpha
alpha=alpha(x)
print(alpha)
"""
tensor([[0.1000, 0.1600, 0.2800],
        [0.0770, 0.1104, 0.0606],
        [0.0419, 0.0355, 0.0528]])
        """
def p(x,alpha):#p(x)
        # alpha=alpha(x);
        return torch.sum(alpha[len(x)-1])
p(x,alpha)
#tensor(0.1302)

def beta(x):
    beta=torch.ones(1,y_size)
    for i in range(len(x)-2,-1,-1):
        beta=torch.cat((torch.sum(beta[0]*transition*b[:,x[i+1]],axis=1).reshape(1,y_size),beta))
    return beta

beta=beta(x)

tensor([[0.2451, 0.2622, 0.2277],
        [0.5400, 0.4900, 0.5700],
        [1.0000, 1.0000, 1.0000]])

def gamma(alpha,beta,p_x):
        return alpha*beta/p_x
def xi(x,alpha,beta,p_x):
    # print(alpha_yt,b[y_t1,x_t1],beta_yt1,transition[y_t,y_t1])
    # return alpha_yt*b[y_t1,x_t1]*beta_yt1*transition[y_t,y_t1]/p_x
    xi=[]
    for t in range(0,len(x)-1):
        xi.append((alpha[t].reshape(y_size,1)*transition*b[:,x[t+1]]*beta[t+1]))
        # print(xi[t])
    return torch.cat(xi).reshape(len(xi),y_size,y_size)

• 求最优路径(维特比，贪心）
  • $\delta (y_1)=\alpha (y_1)=P(x_1|y_1){\pi }_{y_1}$
  • $\delta (y_{t+1})=ma{x}_{y_1}\delta (y_1)P(y_2=1|y_1))P(x_2|y_2)=max(\delta (y_1=1)P(y_2=2|y_1=1),\delta (y_1=2)P(y_2=2|y_1=2),\delta (y_1=3)P(y_2=2|y_1=3))\ast P(x_2|y_2=1)$
• HMM(x–O)
  • 则联合概率$P(x,y)=p(y_1){\Pi }_{t=1}^{T-1}P(y_{t+1}^j|y_t^i){\Pi }_{t=1}^{T}P(x_t|y_t)$
    • 参数化$P(x,y)={\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t)$
  • $$\begin{gathered} P(x)={\Sigma }_{y_1,y_2,...,y_T}P(x,y)={\Sigma }_{y_1,y_2,...,y_T}{\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t) \\ ={\Sigma }_{y}P(x|y)p(y) \\ ={\Sigma }_{y_1}{\Sigma }_{y_2}...{\Sigma }_{y_T}{\pi }_{y_1}{\Pi }_{t=1}^{T-1}{a}_{y_{t+1},y_t}{\Pi }_{t=1}^{T}P(x_t|y_t) \end{gathered}$$
  • $P(y_t|x)=\gamma (y_t)=\frac{P(x1,...,x_t,y_t)P(x_{t+1},...,x_n|y_t)}{P(x)}=\frac{\alpha (y_t)\beta (y_t)}{P(x)}$
  • 递归的计算
    • $\alpha (y_{t+1})={\Sigma }_{y_t}\alpha (y_t)a_{y_{t+1},y_t}P(x_{t+1}|y_{t+1})$
      • 初始化$\alpha (y_0)=P(x_0,y_0)=p(x_0|y_0)P(y_0)=P(x_0|y_0){\pi }_{y_0}$
    • $\beta (y_t)={\Sigma }_{y_{t+1}}\beta (y_{t+1})a_{y_{t+1},y_t}P(x_{t+1}|y_{t+1})$
      • 初始化$\beta (y_T)=1就行了$
        • $假定\beta (y_T)为单位向量，我们可以准确计算出{\beta }_{y_{T-1}}$
          • $P(x)={\Sigma }_i\alpha (y_T^i)\beta (y_T^i)={\Sigma }_i\alpha (y_T^i)=P(x)$

def Viterbi(x):#贪婪
        V=b[:,x[0]]*pi[:].reshape(y_size);
        list=[]
        print("V0:",V)
        # 前向计算各部分概率
        for t in range(1,len(x)):
            # max,indices=torch.max(V[t - 1].reshape(y_size, 1) * transition, axis=0)
            # list.append(indices)
            # V=torch.cat((V,(b[:,x[t]]*max).reshape(1,y_size)),axis=0)
            max, indices = torch.max(V.reshape(y_size,1) * transition, axis=0)
            list.append(indices)
            V=b[:,x[t]]*max
            print("V",t,V)
        #后向寻找路径
        print("max-pathchoice",list)
        max,indices=torch.max(V,axis=0)
        path=indices.reshape(1)
        print(indices)
        for i in range(len(list)-1,-1,-1):
            path=torch.cat((list[0][path[0]].reshape(1),path))
        return path;#y1=path0,y2=path1

print("path",Viterbi(x))

V0: tensor([0.1000, 0.1600, 0.2800])
V 1 tensor([0.0280, 0.0504, 0.0420])
V 2 tensor([0.0076, 0.0101, 0.0147])
max-pathchoice [tensor([2, 2, 2]), tensor([1, 1, 2])]
tensor(2)
path tensor([2, 2, 2])

4.1.5 EM(baum-welch算法)的上溢出和下溢出

通过放缩$\alpha ,\beta$解决