1 精确解释
1.1 因变量采用对数变换
l
n
(
y
^
)
=
β
0
+
β
1
×
x
ln(\hat y)=\beta_0 +\beta_1 \times x
ln(y^)=β0+β1×x
x
→
x
+
1
;
y
^
1
→
y
^
2
x \to x+1; \hat y_1 \to \hat y_2
x→x+1;y^1→y^2
{ y ^ 1 = e β 0 + β 1 × x y ^ 2 = e β 0 + β 1 × ( x + 1 ) \begin{cases} \hat y_1=e^{\beta_0 +\beta_1 \times x}\\ \hat y_2=e^{\beta_0 +\beta_1 \times (x+1)} \end{cases} {y^1=eβ0+β1×xy^2=eβ0+β1×(x+1)
y ^ 2 y ^ 1 = e β 0 + β 1 × ( x + 1 ) e β 0 + β 1 × x = e [ β 0 + β 1 × ( x + 1 ) ] − [ β 0 + β 1 × x ] = e β 1 \begin{aligned} &\frac{\hat y_2}{\hat y_1}\\ &=\frac{e^{\beta_0+\beta_1 \times (x+1)}}{e^{\beta_0+\beta_1 \times x}}\\ &=e^{[\beta_0+\beta_1 \times (x+1)]-[\beta_0+\beta_1 \times x]}\\ &=e^{\beta_1} \end{aligned} y^1y^2=eβ0+β1×xeβ0+β1×(x+1)=e[β0+β1×(x+1)]−[β0+β1×x]=eβ1
结论
- x x x每增加一个单位变为 x + 1 x+1 x+1, y ^ \hat y y^变为原来的 e β 1 e^{\beta_1} eβ1倍
- x x x每增加一个单位变为 x + 1 x+1 x+1, y ^ \hat y y^相比原来增加 [ e β 1 − 1 ] × 100 % [e^{\beta_1}-1]\times 100\% [eβ1−1]×100%
1.2 自变量采用对数变换
y
^
=
β
0
+
β
1
×
l
n
(
x
)
\hat y=\beta_0+\beta_1 \times ln(x)
y^=β0+β1×ln(x)
x
→
e
×
x
;
y
^
1
→
y
^
2
x \to e\times x; \hat y_1 \to \hat y_2
x→e×x;y^1→y^2
{
y
^
1
=
β
0
+
β
1
×
l
n
(
x
)
y
^
2
=
β
0
+
β
1
×
l
n
(
e
×
x
)
\begin{cases} \hat y_1=\beta_0+\beta_1 \times ln(x)\\ \hat y_2=\beta_0+\beta_1 \times ln(e \times x) \end{cases}
{y^1=β0+β1×ln(x)y^2=β0+β1×ln(e×x)
y
^
2
−
y
^
1
=
[
β
0
+
β
1
×
l
n
(
e
×
x
)
]
−
[
β
0
+
β
1
×
l
n
(
x
)
]
=
[
β
0
+
β
1
×
(
l
n
(
e
)
+
l
n
(
x
)
)
]
−
[
β
0
+
β
1
×
l
n
(
x
)
]
=
[
β
0
+
β
1
×
l
n
(
e
)
+
β
1
×
l
n
(
x
)
]
−
[
β
0
+
β
1
×
l
n
(
x
)
]
=
β
1
×
l
n
(
e
)
=
β
1
\begin{aligned} &\hat y_2-\hat y_1 \\ &=[\beta_0+\beta_1 \times ln(e \times x)]-[\beta_0+\beta_1 \times ln(x)]\\ &=[\beta_0+\beta_1 \times (ln(e)+ln(x))]-[\beta_0+\beta_1 \times ln(x)]\\ &=[\beta_0+\beta_1 \times ln(e)+\beta_1 \times ln(x)]-[\beta_0+\beta_1 \times ln(x)]\\ &=\beta_1 \times ln(e)\\ &=\beta_1 \end{aligned}
y^2−y^1=[β0+β1×ln(e×x)]−[β0+β1×ln(x)]=[β0+β1×(ln(e)+ln(x))]−[β0+β1×ln(x)]=[β0+β1×ln(e)+β1×ln(x)]−[β0+β1×ln(x)]=β1×ln(e)=β1
结论
- x x x变为原来的 e e e倍后,则 y ^ \hat y y^增加 β 1 \beta_1 β1
- 如果使用以2为底的对数变换,则 x x x变为原来的2倍后, y ^ \hat y y^增加 β 1 \beta_1 β1
1.3 因变量和自变量同时采用对数变换
l
n
(
y
^
)
=
β
0
+
β
1
×
l
n
(
x
)
ln(\hat y)=\beta_0 +\beta_1\times ln(x)
ln(y^)=β0+β1×ln(x)
x
→
k
×
x
;
y
^
1
→
y
^
2
x \to k \times x; \hat y_1 \to \hat y_2
x→k×x;y^1→y^2
{
y
^
1
=
e
β
0
+
β
1
×
l
n
(
x
)
y
^
2
=
e
β
0
+
β
1
×
l
n
(
k
×
x
)
\begin{cases} \hat y_1=e^{\beta_0+\beta_1\times ln(x)}\\ \hat y_2=e^{\beta_0+\beta_1\times ln(k \times x)} \end{cases}
{y^1=eβ0+β1×ln(x)y^2=eβ0+β1×ln(k×x)
y
^
2
y
^
1
=
e
β
0
+
β
1
×
l
n
(
k
×
x
)
e
β
0
+
β
1
×
l
n
(
x
)
=
e
[
β
0
+
β
1
×
l
n
(
k
×
x
)
]
−
[
β
0
+
β
1
×
l
n
(
x
)
]
=
e
[
β
0
+
β
1
×
l
n
(
k
)
+
β
1
×
l
n
(
x
)
]
−
[
β
0
+
β
1
×
l
n
(
x
)
]
=
e
β
1
×
l
n
(
k
)
=
[
e
l
n
(
k
)
]
β
1
=
k
β
1
\begin{aligned} &\frac{\hat y_2}{\hat y_1}\\ &=\frac{e^{\beta_0+\beta_1\times ln(k \times x)}}{e^{\beta_0+\beta_1\times ln(x)}}\\ &=e^{[\beta_0+\beta_1\times ln(k \times x)]-[\beta_0+\beta_1\times ln(x)]}\\ &=e^{[\beta_0+\beta_1 \times ln(k)+\beta_1 \times ln(x)] - [\beta_0+\beta_1\times ln(x)]}\\ &=e^{\beta_1 \times ln(k)}\\ &=[e^{ln(k)}]^{\beta_1}\\ &=k^{\beta_1} \end{aligned}
y^1y^2=eβ0+β1×ln(x)eβ0+β1×ln(k×x)=e[β0+β1×ln(k×x)]−[β0+β1×ln(x)]=e[β0+β1×ln(k)+β1×ln(x)]−[β0+β1×ln(x)]=eβ1×ln(k)=[eln(k)]β1=kβ1
结论
- x x x变为原来的 k k k倍, y ^ \hat y y^变为原来的 k β 1 k^{\beta_1} kβ1倍
- x x x变为原来的 k k k倍, y ^ \hat y y^增加 [ k β 1 − 1 ] × 100 % [k^{\beta_1} - 1]\times 100\% [kβ1−1]×100%
2 粗略解释
2.1 e β − 1 e^{\beta} - 1 eβ−1与 β \beta β的关系
library(ggplot2)
library(latex2exp)
x <- seq(0, 0.5, 0.001)
y1 <- x
y2 <- exp(x) - 1
df <- data.frame(x = x, y1 = y1, y2 = y2)
ggplot(data = df) +
geom_line(aes(x = x, y = y1, color = "beta"), size = 1) +
geom_line(aes(x = x, y = y2, color = "exp(beta)-1"), size = 1) +
labs(x = TeX('$\\beta$'), y = "Y") +
theme_classic()
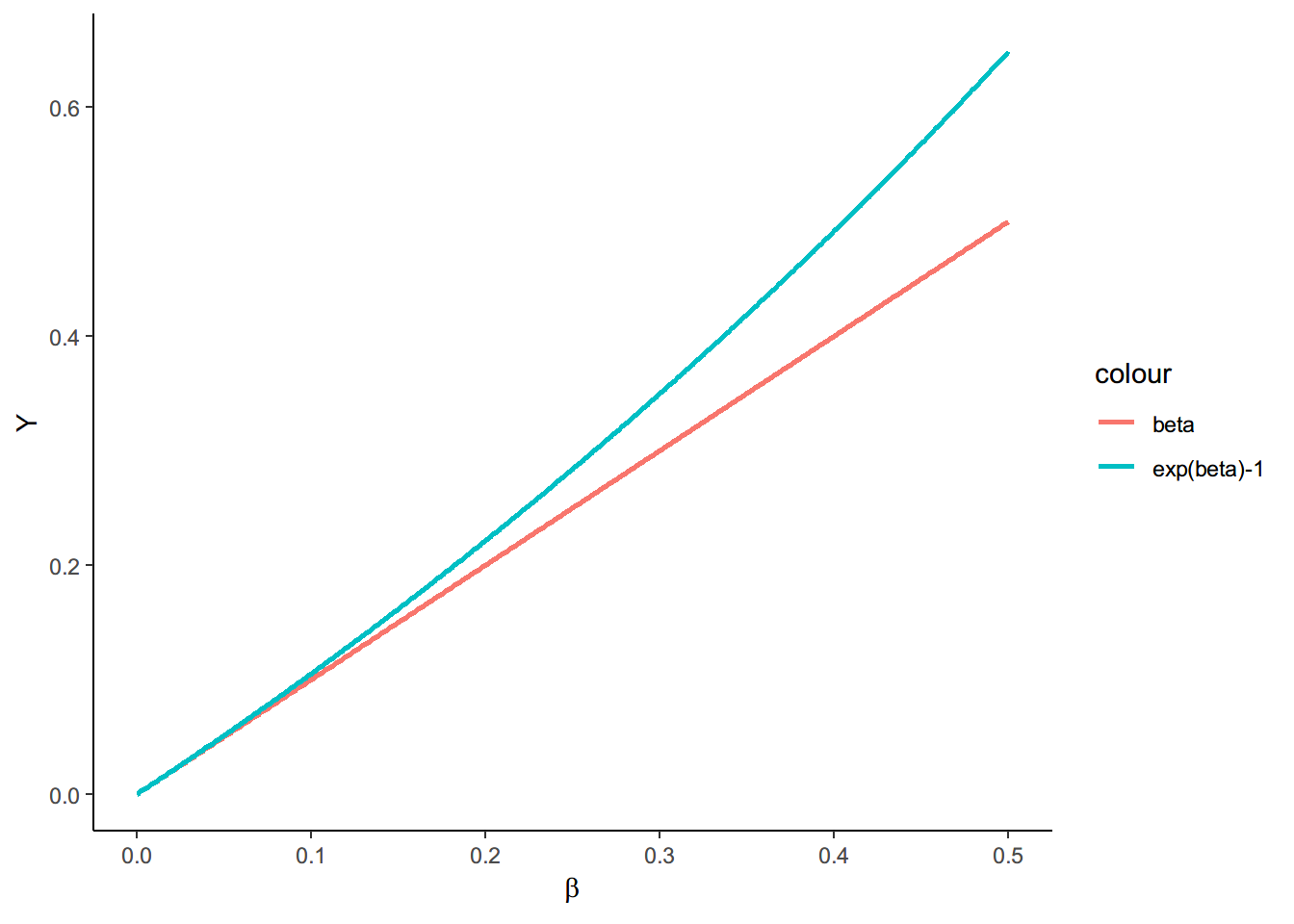
结论
- 当 β \beta β较小时, e β − 1 e^{\beta}-1 eβ−1与 β \beta β的值接近
2.2 因变量采用对数变换
l
n
Y
=
β
1
+
β
2
t
lnY=\beta_1+\beta_2t
lnY=β1+β2t
β
2
=
d
(
l
n
Y
)
d
t
=
d
Y
/
Y
d
t
\beta_2=\frac{d(lnY)}{dt}=\frac{dY/Y}{dt}
β2=dtd(lnY)=dtdY/Y
总结
- β 2 \beta_2 β2测度了 Y Y Y的瞬时变化率
- β 2 \beta_2 β2可粗略解释为: t t t每增加1个单位, Y Y Y增加 β 2 × 100 % \beta_2 \times 100\% β2×100%,如年均增长率。( e β 2 − 1 ≈ β 2 e^{\beta_2}-1\approx\beta_2 eβ2−1≈β2;当 β 2 \beta_2 β2较小时)
2.3 自变量采用对数变换
Y
=
β
1
+
β
2
×
l
n
x
Y=\beta_1+\beta_2 \times lnx
Y=β1+β2×lnx
β
2
=
d
Y
d
(
l
n
x
)
=
d
Y
d
x
/
x
\beta_2=\frac{dY}{d(lnx)}=\frac{dY}{dx/x}
β2=d(lnx)dY=dx/xdY
总结
- β 2 \beta_2 β2测度了 x x x轻微变化(百分比变化)后 Y Y Y的绝对变化量
- β 2 \beta_2 β2可粗略解释为:当 x x x变化 1 % 1\% 1%时, Y Y Y绝对变化 0.01 × β 2 0.01\times \beta_2 0.01×β2
2.4 因变量和自变量同时采用对数变换
l
n
(
Y
)
=
β
1
+
β
2
×
l
n
x
ln(Y)=\beta_1 +\beta_2\times lnx
ln(Y)=β1+β2×lnx
β
2
=
d
(
l
n
Y
)
d
(
l
n
x
)
=
d
Y
/
Y
d
x
/
x
\beta_2=\frac{d(lnY)}{d(lnx)}=\frac{dY/Y}{dx/x}
β2=d(lnx)d(lnY)=dx/xdY/Y
总结
- β 2 \beta_2 β2测度了 Y Y Y对 x x x的弹性,如 Y Y Y为某商品的需求量, x x x为该商品价格, β 2 \beta_2 β2为需求的价格弹性
- β 2 \beta_2 β2可粗略解释为: x x x变动 1 % 1\% 1%引起 Y Y Y变动的百分数
























 2864
2864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








