K-Means和KNN的通俗解释

KNN是什么

其实，KNN也叫K近邻算法，简而言之，可以认为是K个最近的邻居，当K等于1的时候，就是寻找那一个离他最近的邻居。用官方的话来说，所谓K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居），这K个实例的多数属于某个类，就把该输入实例分类到这个类中。
KNN中的核心思想就是当我们无法判定当前待分类的点是属于已知类别中的哪一类时，我们可以根据统计学的理论来看看它所在位置的特征，衡量它周围邻居的权重，最终将它归为权重最大的那一类。

KNN的工作原理：

1.在KNN中，我们需要找到哪个或者哪几个邻居离它最近，那么度量这个远近的标准就是距离，因此，我们需要计算出待分类物体与其他物体之间的距离；
2.统计出距离最近的K个邻居；
3.对于K个最近的邻居，它们属于哪个分类最多，那么它们就属于哪一个分类。

距离的计算公式：

1.欧氏距离

欧氏距离，也叫欧几里得距离，是我们最常用的距离公式，用于表示两点之间或多点之间的距离：

在二维空间中则是：

2.曼哈顿距离

曼哈顿距离在几何空间中使用的比较多。要注意的是，曼哈顿距离依赖座标系统的转度，而非系统在座标轴上的平移或映射。
通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”，此即曼哈顿距离名称的来源， 同时，曼哈顿距离也称为城市街区距离它的公式如下：

如果绿线表示两点之间的欧式距离，那么红线和黄线就表示曼哈顿距离了。

3.切比雪夫距离

切比雪夫距离就是两点坐标之间绝对值相差最大的距离，和上面的曼哈顿距离有些类似。

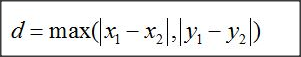
图一就是曼哈顿距离地集合，图二则为切比雪夫距离

4.余弦距离

在数学几何中，夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。在文本分类中，我们会经常遇到余弦距离。余弦距离实际上就是计算两个向量的夹角，也就是在方向上计算两者之间的差异，不管绝对值相差多大，都不对它造成影响。在推荐算法中的感兴趣的相关性比较上，角度的关系比距离的绝对值还要重要，所以在推荐、文本分类中，经常会使用到余弦距离。

5.闵可夫斯基距离

闵可夫斯基不是一个距离，而是一组距离，对于n维空间中的两个点x（x1,x2…）,y(y1,y2…)，他们的距离公式为下图所示。其中p是一个变参数。 当p=1时，就是曼哈顿距离 当p=2时，就是欧氏距离 当p→∞时，就是切比雪夫距离。根据变参数的不同，闵氏距离可以表示一类的距离。

K-Means的工作原理：

首先我们需要选择K个类中心点，这些点一般是从数据集中随机抽取出来的；
然后将每一个样本都分配到离它最近的类中心点，这么就形成了K个类，然后重新再计算每个类的中心点；
一直重复上一步，直到类不发生变化，或者你也可以设置最大迭代次数，当达到这个迭代次数的时候，就会结束运行。

和KNN一样，也是通过距离来计算出应该归到哪一个类；这里的计算距离也有以上几种方式。

两者的区别与联系：

1.它们都是用于解决数据挖掘的算法。K-Means是聚类算法，KNN是分类算法。
2.K-Means是非监督学习，KNN是有监督学习。是否为监督学习在于看是否需要我们给出训练数据的分类标识。
3.K-Means中的K代表K类，而KNN中的K代表K个最近的邻居。

一个问题：

你知道为什么在k-means或kNN，我们是用欧氏距离来计算最近的邻居之间的距离。为什么不用曼哈顿距离？

因为曼哈顿距离它只计算水平或垂直距离，有维度的限制。另一方面，欧式距离可用于任何空间的距离计算问题。因为，数据点可以存在于任何空间，欧氏距离是更可行的选择。例如：想象一下国际象棋棋盘，象或车所做的移动是由曼哈顿距离计算的，因为它们是在各自的水平和垂直方向的运动。

KNN的python实现

import numpy as np
import operator

def knn(trainData, testData, labels, k):
    # 计算训练样本的行数
    rowSize = trainData.shape[0]
    # 计算训练样本和测试样本的差值
    diff = np.tile(testData, (rowSize, 1)) - trainData
    # 计算差值的平方和
    sqrDiff = diff ** 2
    sqrDiffSum = sqrDiff.sum(axis=1)
    # 计算距离
    distances = sqrDiffSum ** 0.5
    # 对所得的距离从低到高进行排序
    sortDistance = distances.argsort()

    count = {}

    for i in range(k):
        vote = labels[sortDistance[i]]
        count[vote] = count.get(vote, 0) + 1
    # 对类别出现的频数从高到低进行排序
    sortCount = sorted(count.items(), key=operator.itemgetter(1), reverse=True)

    # 返回出现频数最高的类别
    return sortCount[0][0]

#第一个参数为打戏，第二个为吻戏
trainData = np.array([[5, 1], [4, 0], [1, 3], [0, 4]])
labels = ['动作片', '动作片', '爱情片', '爱情片']
testData = [3, 2]
X = knn(trainData, testData, labels, 3)
print(X)

**K-Means的python实现：**

```python
import numpy as np
from matplotlib import pyplot


class K_Means(object):
    # k是分组数；tolerance‘中心点误差’；max_iter是迭代次数
    def __init__(self, k=2, tolerance=0.0001, max_iter=300):
        self.k_ = k
        self.tolerance_ = tolerance
        self.max_iter_ = max_iter

    def fit(self, data):
        self.centers_ = {}
        for i in range(self.k_):
            self.centers_[i] = data[i]

        for i in range(self.max_iter_):
            self.clf_ = {}
            for i in range(self.k_):
                self.clf_[i] = []
            # print("质点:",self.centers_)
            for feature in data:
                # distances = [np.linalg.norm(feature-self.centers[center]) for center in self.centers]
                distances = []
                for center in self.centers_:
                    # 欧拉距离
                    # np.sqrt(np.sum((features-self.centers_[center])**2))
                    distances.append(np.linalg.norm(feature - self.centers_[center]))
                classification = distances.index(min(distances))
                self.clf_[classification].append(feature)

            # print("分组情况:",self.clf_)
            prev_centers = dict(self.centers_)
            for c in self.clf_:
                self.centers_[c] = np.average(self.clf_[c], axis=0)

            # '中心点'是否在误差范围
            optimized = True
            for center in self.centers_:
                org_centers = prev_centers[center]
                cur_centers = self.centers_[center]
                if np.sum((cur_centers - org_centers) / org_centers * 100.0) > self.tolerance_:
                    optimized = False
            if optimized:
                break

    def predict(self, p_data):
        distances = [np.linalg.norm(p_data - self.centers_[center]) for center in self.centers_]
        index = distances.index(min(distances))
        return index


if __name__ == '__main__':
    x = np.array([[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]])
    k_means = K_Means(k=2)
    k_means.fit(x)
    print(k_means.centers_)
    for center in k_means.centers_:
        pyplot.scatter(k_means.centers_[center][0], k_means.centers_[center][1], marker='*', s=150)

    for cat in k_means.clf_:
        for point in k_means.clf_[cat]:
            pyplot.scatter(point[0], point[1], c=('r' if cat == 0 else 'b'))

    predict = [[2, 1], [6, 9]]
    for feature in predict:
        cat = k_means.predict(predict)
        pyplot.scatter(feature[0], feature[1], c=('r' if cat == 0 else 'b'), marker='x')

    pyplot.show()