动态规划理论及笔试题

动态规划(Dynamic Programming)

1.理论定义

• 简称 dp
• 动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。不像搜索或数值计算那样，具有一个标准的数学表达式和明确清晰的解题方法。动态规划程序设计往往是针对一种最优化问题，由于各种问题的性质不同，确定最优解的条件也互不相同，因而动态规划的设计方法对不同的问题，有各具特色的解题方法，而不存在一种万能的动态规划算法，可以解决各类最优化问题。因此读者在学习时，除了要对基本概念和方法正确理解外，必须具体问题具体分析处理，以丰富的想象力去建立模型，用创造性的技巧去求解。我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论，逐渐学会并掌握这一设计方法。
• 动态规划一般可分为线性动规，区域动规，树形动规，背包动规四类。

2.解决的问题的基本思想

		 动态规划程序设计主要是用于求一些问题的最优解

首先来了解一下动态规划中的术语

1. 阶段：就是把整个解题过程分解成若干个阶段

   	例如坐火车从北京到深圳，每次的经停一个地方都是一个阶段
   

2. 状态：状态表示每个阶段开始面临的自然状况或客观条件，它不以人们的主观意志为转移，也称为不可控因素

3. 无后效性：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响，所有各阶段都确定时，整个过程也就确定

4. 决策：一个阶段的状态给定以后，从该状态演变到下一阶段某个状态的一种选择（行动）称为决策。在最优控制中，也称为控制

5. 策略：由每个阶段的决策组成的序列称为策略

   	策略集合：中达到最优解的策略称为最优策略
   

解决问题的基本模型

• 根据上例分析和动态规划的基本概念，可以得到动态规划的基本模型如下：

1. 确定问题的决策对象。

2. 对决策过程划分阶段。

3. 对各阶段确定状态变量。

4. 根据状态变量确定费用函数和目标函数。

5. 建立各阶段状态变量的转移过程，确定状态转移方程。

    状态转移方程的一般形式：
    		一般形式： U：状态； X：策略
    顺推：
    		f[Uk]=opt{f[Uk-1]+L[Uk-1,Xk-1]} 
    		L[Uk-1,Xk-1]： 状态Uk-1通过策略Xk-1到达状态Uk 的费用 
    		初始f[U1]；
    		结果：f[Un]。
    倒推：  
    		f[Uk]=opt{f[Uk+1]+L[Uk,Xk]}
    		L[Uk,Xk]： 状态Uk通过策略Xk到达状态Uk+1 的费用
    		初始f[Un]；结果：f(U1)
   

应用实际

经典问题：求数字三角形的最大路径和
难度：简单
该题如图:

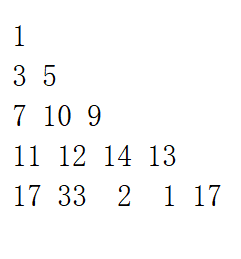
输入这样的数字三角形，输出的最大和：33+12+10+5+1=61

所以要解这个问题，就是确定何种方式能找到最大路径和，所以这个时候我们可以创建一个二维矩阵
这也是我们解决动态规划问题的常用方式

解题思路：

此时我们可以定义每个矩阵的数值为：D[i][j]
最大路径和为：max_sum[i] [j]

通常解题方式：

通常我们找最大路径都是从第一行开始找，然后向下找，从而找最大值，并且记录每一行的最大值
这中情况下我们的状态方程就是max_sum[ i ][ j ] = max( sum_sum[i+1][j],sum[i+1][j+1])+D[i][j];
不过在这种情况下，我们需要记录每一个点的路径和，过于消耗空间资源
如图所示：

优化后的解题方式:

• 优化方式：从最后一行向前递推
• 并且这时我们也不再需要二维矩阵记录最大值max_sum[i][j]，
• 只需要一维矩阵max_sum[n]就可以了，记录从最后一行开始每一个最大值的变化
• 解题思路如图
  
  思路清晰以后我们可以轻松的写出代码：

#include<bits/stdc++.h>
using namespace std; 
int main(){    
	int n; 
	
	int i,j;  
	cin >> n;
	vector<int>max_sum(n+1);
	vector<vector<int>> dp(n+1,vector<int>(n+1));
   
	for(i=1;i<=n;i++)   
	for (j = 1; j <= i; j++)
	{
	
		cin >> dp[i][j];
		if (i == n){
			max_sum[j] = dp[i][j];
		}
	}
	for (int i = n - 1; i > 0; --i)
	for (int j = 1; j <= i; ++j)
		max_sum[j] = max(max_sum[j], max_sum[j + 1]) + dp[i][j];
		cout << max_sum[1] << endl;
	system("pause");
	return 0;
} 
}