g
(
τ
)
g(\tau )
g(τ) is an even function,
(
g
(
−
τ
)
=
g
(
τ
)
)
(g(-\tau)=g(\tau) )
(g(−τ)=g(τ)), so convolution is equivalent to correlation.
convolution
(
f
∗
g
)
(
t
)
=
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
d
τ
 
.
(f∗g)(t) = \int_{-∞}^{∞} f (τ) g (t-τ) dτ\,.
(f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ.
cross-correlation
(
f
⋆
g
)
(
τ
)
=
∫
−
∞
∞
f
(
t
)
‾
g
(
t
+
τ
)
d
t
 
.
(f \star g)(τ) = \int_{-∞}^{∞} \overline{f (t)} g (t+τ) dt\,.
(f⋆g)(τ)=∫−∞∞f(t)g(t+τ)dt.
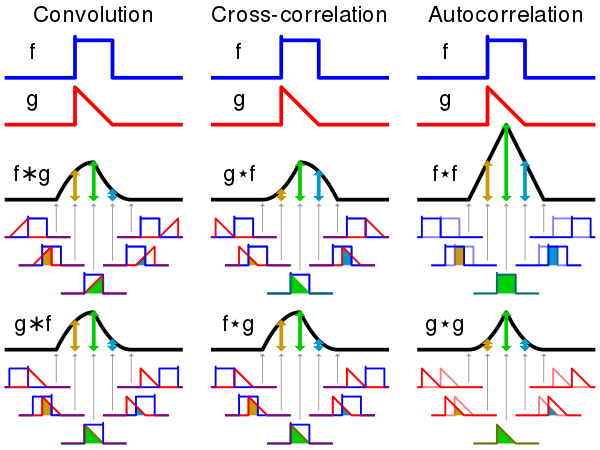
1.Express each function in terms of a dummy variable τ \tau τ. 2.Reflect one of the functions: g ( τ ) g(\tau ) g(τ)→ g ( − τ ) . g(-\tau ). g(−τ). 3.Add a time-offset, t, which allows g ( t − τ ) g(t-\tau ) g(t−τ) to slide along the τ \tau τ -axis. 4.Start t at −∞ and slide it all the way to +∞. Wherever the two functions intersect, find the integral of their product. In other words, compute a sliding, weighted-sum of function f ( τ ) f(\tau ) f(τ), where the weighting function is g ( − τ ) . g(-\tau ). g(−τ).
|  |
In this example, the red-colored “pulse”, g ( τ ) g(\tau ) g(τ),is an even function ( g ( − τ ) = g ( τ ) ) (g(-\tau)=g(\tau) ) (g(−τ)=g(τ)), so convolution is equivalent to correlation. A snapshot of this “movie” shows functions g ( t − τ ) g(t-\tau ) g(t−τ)and f ( τ ) f(\tau ) f(τ) (in blue) for some value of parameter t t t, which is arbitrarily defined as the distance from the τ = 0 \tau =0 τ=0 axis to the center of the red pulse. The amount of yellow is the area of the product f ( τ ) ⋅ g ( t − τ ) f(\tau )\cdot g(t-\tau ) f(τ)⋅g(t−τ), computed by the convolution/correlation integral. The movie is created by continuously changing t t t and recomputing the integral. The result (shown in black) is a function of t t t, but is plotted on the same axis as τ \tau τ , for convenience and comparison. |  |
In this depiction, f ( τ ) f(\tau ) f(τ) could represent the response of an RC circuit to a narrow pulse that occurs at τ = 0 \tau =0 τ=0. In other words, if g ( τ ) = δ ( τ ) g(\tau )=\delta (\tau ) g(τ)=δ(τ), the result of convolution is just f ( t ) f(t) f(t). But when g ( τ ) g(\tau ) g(τ) is the wider pulse (in red), the response is a “smeared” version of f ( t ) f(t) f(t). It begins at t = − 0.5 t=-0.5 t=−0.5, because we defined t t t as the distance from the τ = 0 \tau =0 τ=0 axis to the center of the wide pulse (instead of the leading edge). |  |
Convolution https://en.wikipedia.org/wiki/Convolution
Cross-correlation https://en.wikipedia.org/wiki/Cross-correlation







 本文深入探讨了信号处理中的两个核心概念:卷积和互相关。解释了卷积如何通过将一个函数翻转并平移,与另一个函数相乘并积分来实现,而互相关则直接将两个函数相乘并积分,无需翻转。并通过一个具体的例子,展示了当一个函数为偶函数时,卷积等价于互相关的过程。
本文深入探讨了信号处理中的两个核心概念:卷积和互相关。解释了卷积如何通过将一个函数翻转并平移,与另一个函数相乘并积分来实现,而互相关则直接将两个函数相乘并积分,无需翻转。并通过一个具体的例子,展示了当一个函数为偶函数时,卷积等价于互相关的过程。
















 349
349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








