数学建模之蒙特卡洛算法初探

最新推荐文章于 2024-08-04 14:37:10 发布

NeroChang

最新推荐文章于 2024-08-04 14:37:10 发布

阅读量1.4k

点赞数 4

分类专栏：数学建模蒙特卡洛算法文章标签：数学建模蒙特卡洛算法

本文链接：https://blog.csdn.net/weixin_41122036/article/details/99963267

版权

本文介绍了蒙特卡洛算法在数学建模中的应用，通过求π值、定积分等实例，详细阐述了算法原理及MATLAB实现，展示了如何利用随机抽样估算复杂问题的解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数学建模常用算法–蒙特卡洛算法

简介：蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。
蒙特卡罗方法（随机取样法）是一种计算方法。原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。
步骤：
- 1、人为构造或描述问题的概率过程
- 2、从已知概率分布中进行抽样（随机变量抽样）
- 3、求各统计量的估计
- 4、使用统计量的估计最终求近似解

例1、求 $\pi$ 值

题目：正方形内部有一个相切的圆，它们的面积之比是π/4。现在，在这个正方形内部，随机产生1000000个点（即1000000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。
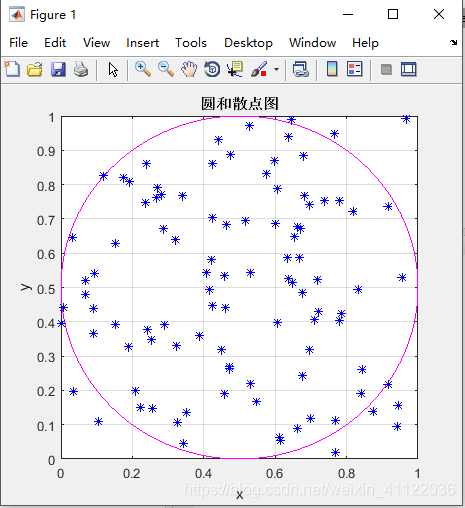
在这里插入图片描述
matlab实现：

%圆与正方形面积之比
tic
N=10000000;    %随机点的数目
x=rand(N,1);  %rand 生成均匀分布的伪随机数。分布在（0~1）之间
y=rand(N,1);  %矩阵的维数为N×1
count=0;

for i=1:N
%如果点在圆内，计数器加1
	if (x(i) - 0.5)^2 + (y(i)-0.5)^2 <= 0.25
		count = cou