AcWing 算法基础课学习记录（Python，备战蓝桥杯）Day61 - Day64

Day61.(2021.12.22) 

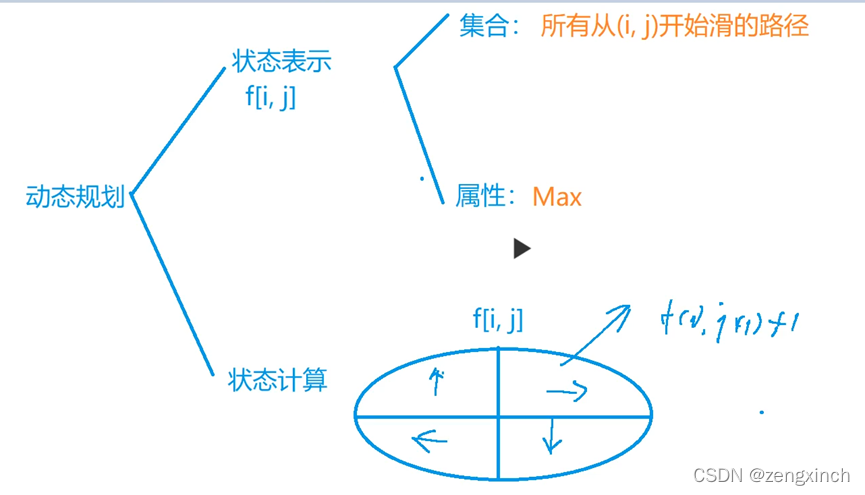
# acwing 901. 滑雪

N = 310
directions = [(-1,0), (1,0), (0,1), (0,-1)]

def dp(x, y):
    if f[x][y]!=-1: return f[x][y]

    f[x][y] = 1
    for direction in directions:
        a, b = x + direction[0], y + direction[1]
        if a>=1 and a<=n and b>=1 and b<=m and w[x][y]>w[a][b]:
            f[x][y] = max(f[x][y], dp(a,b)+1)
    return f[x][y]

if __name__ == '__main__':
    f, w = [[-1]*N for _ in range(N)], [[0]]
    n, m = map(int, input().split())
    for i in range(1,n+1):
        w.append([0] + [int(x) for x in input().split()])

    res = 0
    for i in range(1,n+1):
        for j in range(1,m+1):
            res = max(res, dp(i,j))
    print(res)

Day62.(2021.12.23) 

只有一个问题是单峰的时候才可以用贪心算法

 

 

 

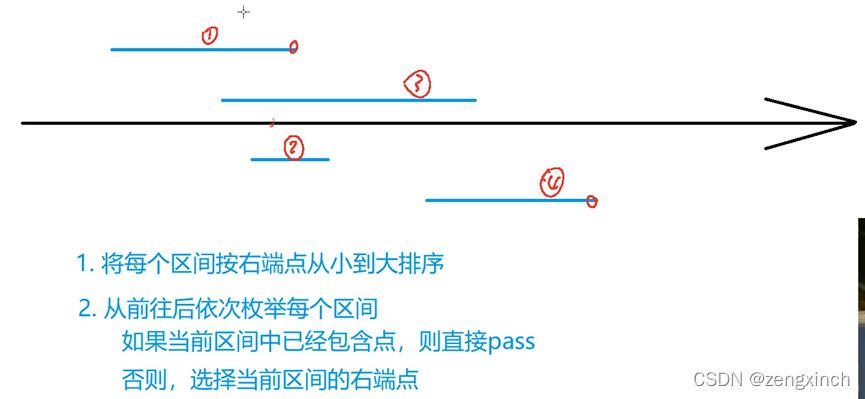
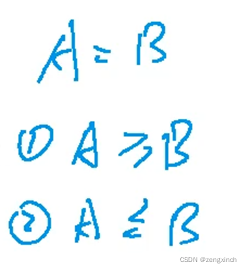
# acwing 905. 区间选点

N = 100010

if __name__ == '__main__':
    n, w = int(input()), []
    for _ in range(n):
        w.append([int(x) for x in input().split()])
    res, r = 0, -2e9
    w.sort(key=lambda x: x[1])

    for sec in w:
        if r<sec[0]:
            res += 1
            r = sec[1]
    print(res)

1.ans>=cnt：因为cnt是一组合理的解，所以cnt<=ans

2.ans<=cnt：按照这种套路选完后，每个区间至少包含一个这样的点（这道题没听懂y总讲的，按照这句话何905的思路，这样做完后，每个区间至少有一个点，那么不存在某一个区间可以被选，但是没有选的情况，所以它就是最大的）

# acwing 908. 最大不相交区间数量

N = 100010

if __name__ == '__main__':
    n, w = int(input()), []
    for _ in range(n):
        w.append([int(x) for x in input().split()])
    res, r = 0, -2e9
    w.sort(key=lambda x: x[1])

    for sec in w:
        if r<sec[0]:
            res += 1
            r = sec[1]
    print(res)

ans:最终答案

cnt:按照给定的贪心算法得到的答案

1 ans<=cnt

首先cnt一定是合法方案（不一定是最小的），每个组内的区间没有任何交集

ans是所有方案中的最小值，所以ans<=cnt

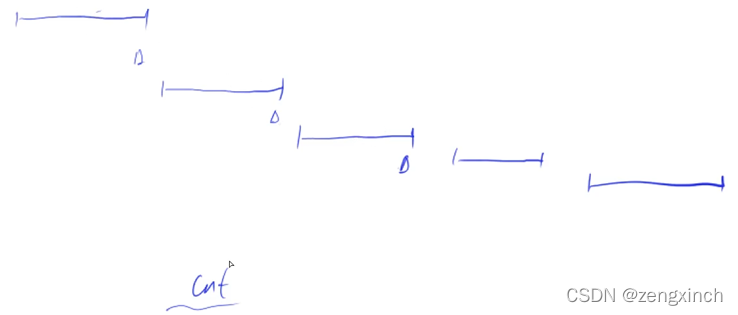
2 ans>=cnt

假设枚举到第i个区间时，打算把这个区间放到某个组内，但前cnt-1个组中都有区间与当前区间有交集，说明至少有cnt个区间有公共点Li​​，所以这cnt个区间一定不会放到同一组中，所以ans>=cnt（所有可行方案组的数量一定是>=cnt，因为每个区间都要单独在一个组里面）

# acwing 906. 区间分组

from heapq import *

if __name__ == '__main__':
    n, w = int(input()), []
    for _ in range(n):
        w.append([int(x) for x in input().split()])
    w.sort(key=lambda x: x[0])

    heap = []
    for i in range(n):
        l, r = w[i]
        if not heap or heap[0]>=l: heappush(heap,r)
        else: heapreplace(heap,r)
    print(len(heap))

 

 贪心问题一般都是，先按左端点或右端点排下序，然后再试几个例子，然后再证明。

# acwing 907. 区间覆盖


if __name__ == '__main__':
    s, t = map(int, input().split())
    n, a = int(input()), []
    for _ in range(n):
        a.append([int(x) for x in input().split()])
    a.sort(key=lambda x:x[0])

    flag, i, res = False, 0, 0
    while i<n:
        r = -2e9
        while i<n and a[i][0] <= s:
            r, i = max(r, a[i][1]), i+1
        if r < s: break

        res, s = res+1, r
        if r>=t:
            flag = True
            break

    if not flag: res = -1
    print(res)


#···································································

if __name__ == '__main__':
    st, ed = map(int, input().split())
    n, w = int(input()), []
    for _ in range(n):
        w.append([int(x) for x in input().split()])
    w.sort(key=lambda x:x[0])

    res, i, flag = 0, 0, False
    while i<n:
        j, r = i, -2e9
        while j<n and w[j][0]<=st:
            r, j = max(r, w[j][1]), j+1
        if r<st: break
        res += 1
        if r>=ed:
            flag = True
            break
        st, i = r, j
    
    if not flag: res = -1
    print(res)

Day63.(2021.12.24) 

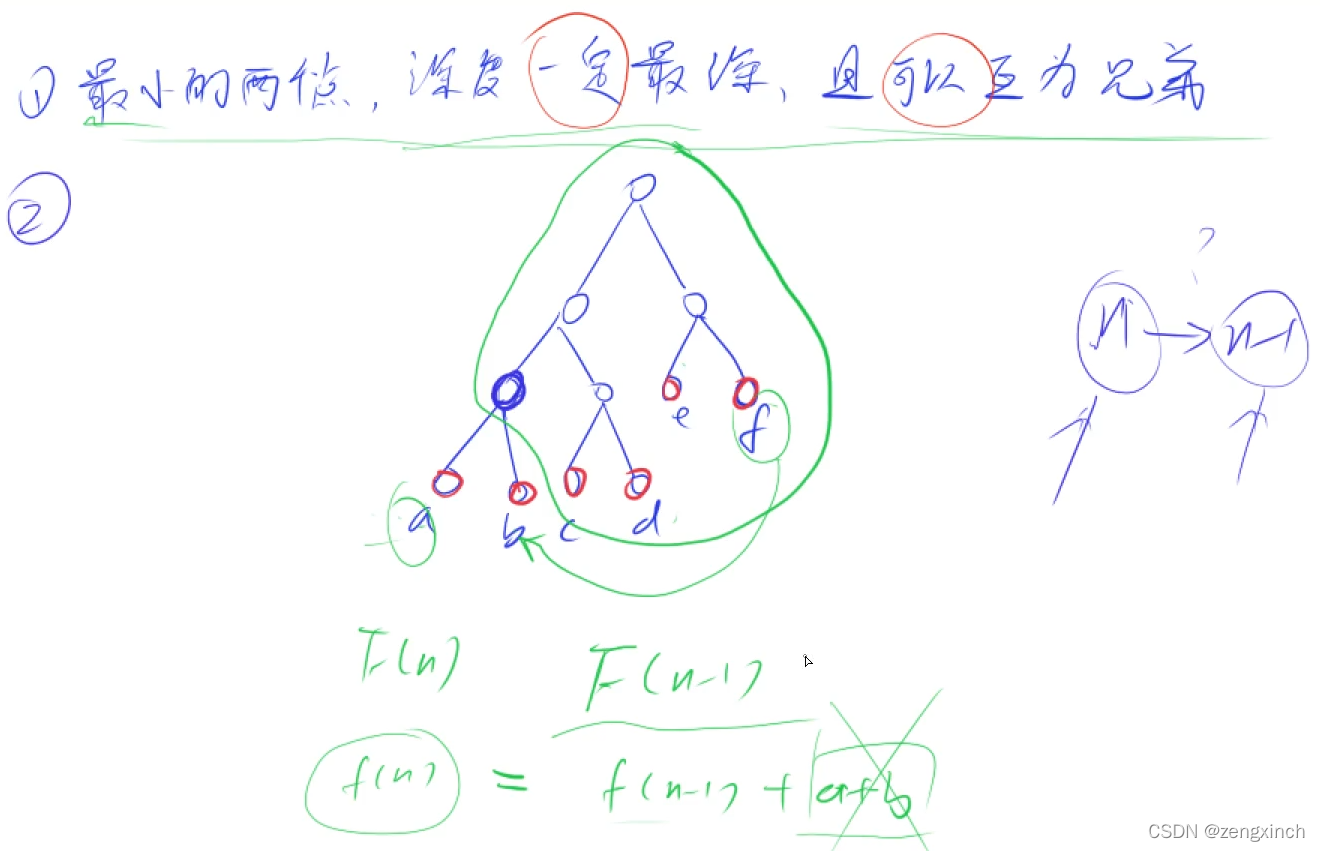
# acwing 148. 合并果子
from heapq import *

if __name__ == '__main__':
    n, res = int(input()), 0
    w = [int(x) for x in input().split()]
    heapify(w)

    while len(w)>1:
        a, b = heappop(w), heappop(w)
        res += a+b
        heappush(w,a+b)
    print(res)

# acwing 913. 排队打水

if __name__ == '__main__':
    n = int(input())
    w = [0] + [int(x) for x in input().split()]
    w.sort()

    res = 0
    for i in range(1,n+1):
        res += w[i]*(n-i)
    print(res)

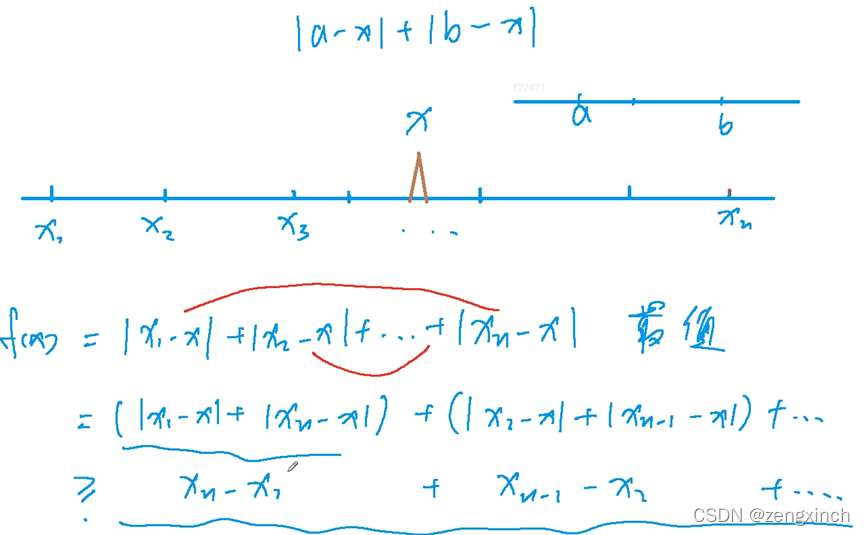
# acwing 104. 货舱选址

if __name__ == '__main__':
    n = int(input())
    w = [int(x) for x in input().split()]
    w.sort()

    res = 0
    for i in range(n):
        res += abs(w[n//2]-w[i])
    print(res)

 

si<wi+si, w(i+1)+s(i+1)<wi+si, 因此交换后的最大值小于交换前的最大值，故风险下降

# acwing 125. 耍杂技的牛

if __name__ == '__main__':
    n, ws = int(input()), []
    for _ in range(n):
        ws.append([int(x) for x in input().split()])
    ws.sort(key=lambda x: x[0]+x[1])

    res, sum = -1e9, 0
    for i in range(n):
        res = max(res, sum-ws[i][1])
        sum += ws[i][0]
    print(res)

Day64.(2021.12.25) 

今天把时空复杂度分析看了后发现竟然还有道题搞忘做了。。

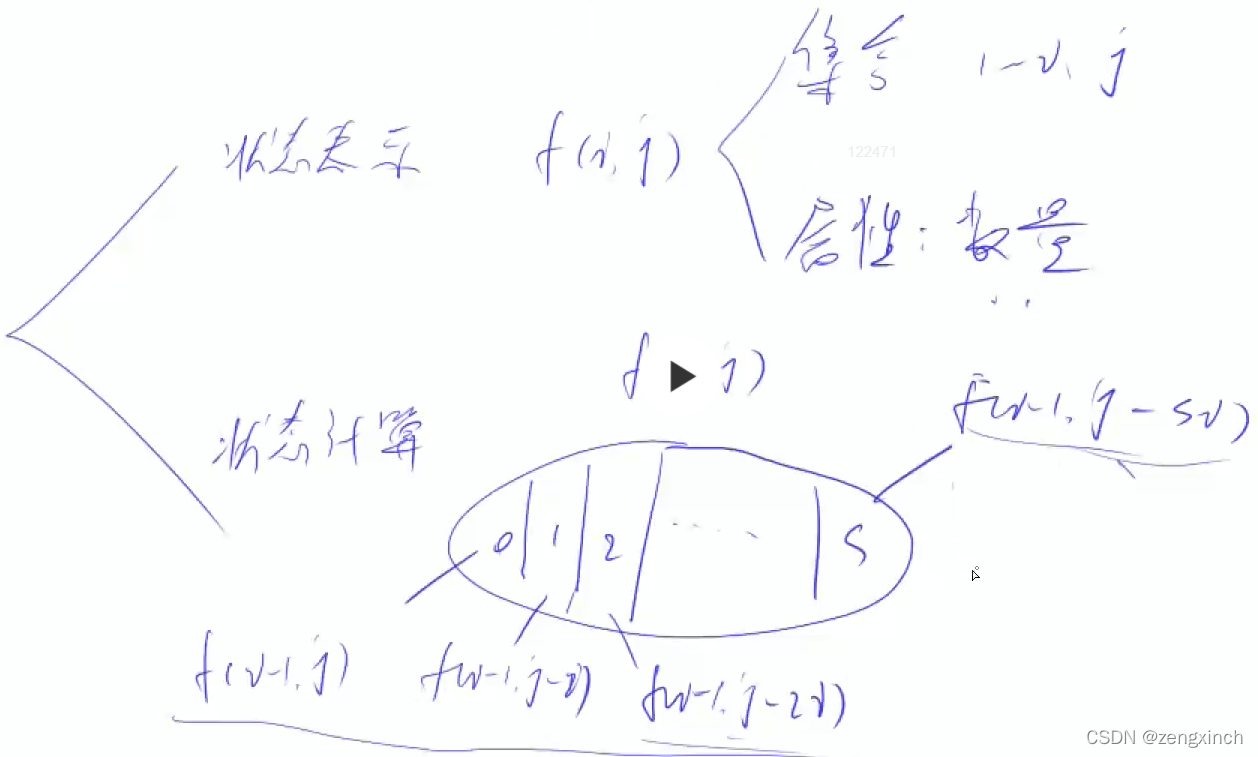
        f[i][j]表示只从1~i中选，且总和等于j的方案数

# acwing 900. 整数划分
N, M = 1010, int(1e9+7)

if __name__ == '__main__':
    f = [[0]*N for _ in range(N)]
    n = int(input())

    for i in range(n+1):
        f[i][0] = 1

    for i in range(1,n+1):
        for j in range(1,n+1):
            for k in range(j//i+1):
                f[i][j] = (f[i][j] + f[i-1][j-k*i])%M

    print(f[n][n])


# -----------------------------------------------------------------
if __name__ == '__main__':
    f = [[0]*N for _ in range(N)]
    n = int(input())

    for i in range(n+1):
        f[i][0] = 1

    for i in range(1,n+1):
        for j in range(1,n+1):
            if j<i: f[i][j] = f[i-1][j]%M
            else: f[i][j] = (f[i-1][j] + f[i][j-i])%M

    print(f[n][n])

# -----------------------------------------------------------------
N, M = 1010, int(1e9+7)

if __name__ == '__main__':
    f = [0]*N
    n, f[0] = int(input()), 1

    for i in range(1,n+1):
        for j in range(1,n+1):
            if j<i: f[j] = f[j]%M
            else: f[j] = (f[j] + f[j-i])%M

    print(f[n])

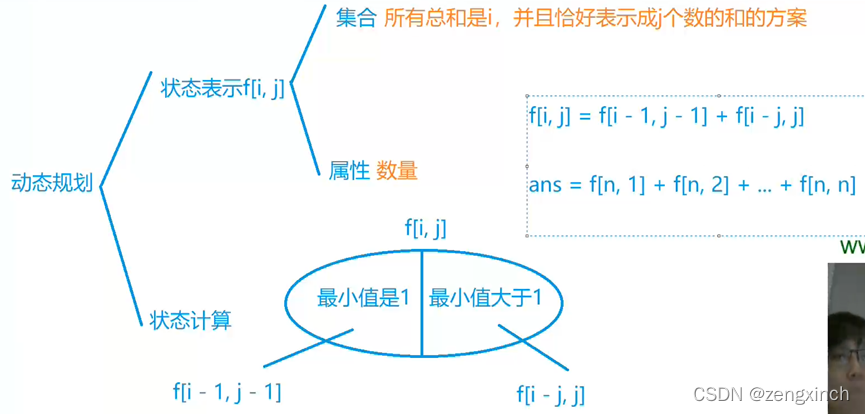
 f[i][j]表示总和为i，总个数为j的方案数

N, M = 1010, int(1e9+7)

if __name__ == '__main__':
    f = [[0]*N for _ in range(N)]
    n = int(input())

    f[1][1] = f[0][0] = 1

    for i in range(2,n+1):
        for j in range(1,n+1):
            f[i][j] = (f[i-1][j-1] + f[i-j][j]) % M

    res = 0
    for i in range(1,n+1):
        res = (res + f[n][i]) % M
    print(res)