道路工程测量中涉及基本概念
道路工程测量分为路线勘察设计测量和道路施工测量。勘察设计测量在道路设计阶段,由勘察设计部门完成。
勘察设计测量
初测
初测内容包括控制测量、测带状地形图和纵断面图、手机沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
定测
在选定设计方案的路线上进行路线中线测量、测纵断面图、横断面图及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
道路施工测量
按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。道路曲线编程计算过程主要就是指利用设计数据计算路线上任意位置的里程和坐标,为施工提供数据基础。
控制测量
根据道路工程的需要,进行平面控制测量和高程控制测量。平面控制测量用于确定道路的平面位置,高程控制测量用于控制道路的纵向坡度和横向路拱坡度。
中线测量
恢复道路中线,包括直线段和曲线段中线测设。通过计算曲线段的主点元素和细部点坐标,确保道路中线的准确位置。
纵断面测量
测绘道路的纵断面和横断面图,为路基、路面的设计和施工提供依据。测量纵断面的高程变化和横断面的宽度、坡度等参数。
施工放样
根据设计图纸和控制测量成果,将道路的中心线、边线、高程等要素准确地放样到实地,为施工提供具体的定位依据。
道路曲线测设
道路线型
道路线型是道路设计的重要组成部分,主要包括直线、平曲线和竖曲线。这些线型的合理设计和测设对于道路行车安全、舒适和施工质量至关重要。通常,道路线型是指道路平面线型、纵断面线型以及二者结合的三维空间线型的总称。
里程桩mileage peg:也成中桩,表示该桩距离路线起点的距离。
- 直线
直线是道路中线的一种基本形式,具有固定的曲率半径(无穷大)。 - 平曲线
- 圆曲线:圆曲线是道路中线的一种基本曲线形式,具有固定的曲率半径。其特点是在曲线上任一点的曲率半径R为常数。
- 缓和曲线:缓和曲线设置在直线与圆曲线之间或半径相差较大的两个同向圆曲线之间,用于使路线的平面线形更加符合汽车的行驶轨迹,确保行车安全和舒适。缓和曲线包括完整缓和曲线和非完整曲线。
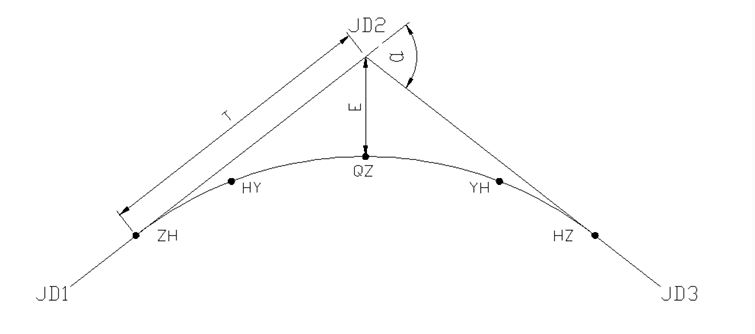
交点JD:路线的转折点,即两个方向直线的交点,用JD表示。
曲线要素:- 转角 α α α:指路线由一个方向偏向另一个方向事,偏转后的方向与原方向的夹角。当偏转后的方向在原方向的左侧,成为左转角;反之为右转角。
- 缓和曲线长度 L s L_s Ls:设计文件给定数据;
- 内移距
p
p
p:内移距是指缓和曲线起点到直线与缓和曲线切线的垂直距离(根据精度要求选择泰勒展开的前几项),
p
=
L
s
2
24
R
−
L
s
4
2688
R
3
p = \frac{L_{s}^2}{24R} - \frac{L{s}^{4}}{2688R^{3}}
p=24RLs2−2688R3Ls4
有点地方第二项前面是“+”,第二项影响不大,此处以《工程测量》教材为依据。 - 切线增长 q q q:切线增长是指缓和曲线终点到圆曲线起点的切线长度增加量(根据精度要求选择泰勒展开的前几项), q = L s 2 − L s 3 240 R 2 + L s 5 34560 R 4 q = \frac{L_s}{2} - \frac{L_{s}^{3}}{240R^{2}} + \frac{L_{s}^{5}}{34560R^{4}} q=2Ls−240R2Ls3+34560R4Ls5
- 切线 T T T:指直线段到缓和曲线起点的距离, T = ( R + p ) ∗ t a n ( α 2 ) + q T = (R + p) * tan(\frac{\alpha}{2}) + q T=(R+p)∗tan(2α)+q
- 圆曲线长 L c L_c Lc:曲线中圆曲线的长度, L c = R α π 180 − L s 1 2 − L s 2 2 L_c = R \frac{\alpha\pi}{180} - \frac{Ls_1}{2} - \frac{Ls_2}{2} Lc=R180απ−2Ls1−2Ls2
- 曲线全长 L L L:圆曲线长与缓和曲线长的和, L = L s 1 + L s 2 + L c L = Ls_1 + Ls_2 + L_c L=Ls1+Ls2+Lc
- 切曲差 D D D:指切线长减去曲线长, D = 2 T − L D = 2T - L D=2T−L
注意:当前后缓和曲线长度不一致时(即非对称缓和曲线),切线长计算方法按下面方法计算,多了
m
=
p
1
−
p
2
sin
α
m = \frac{p_1 - p_2}{\sin \alpha}
m=sinαp1−p2;当路线是右转时,
T
1
=
T
H
1
−
m
T_1 =T_{H1}-m
T1=TH1−m,
T
2
=
T
H
2
+
m
T_2=T_{H2}+m
T2=TH2+m;当路线左转时,
T
1
=
T
H
1
+
m
T_1 =T_{H1}+m
T1=TH1+m,
T
2
=
T
H
2
−
m
T_2 =T_{H2}-m
T2=TH2−m。

道路主点里程的计算
| 主点名称 | 符号 | 描述 | 计算逻辑 |
|---|---|---|---|
| 直缓点 | ZH | 直线段与缓和曲线的连接点 | 前切线方向从交点(JD)回退前切线长 T 1 T_1 T1 |
| 缓圆点 | HY | 缓和曲线与圆曲线的连接点 | ZH点里程 + 前缓和曲线长 L s 1 Ls_1 Ls1 |
| 曲中点 | QZ | 圆曲线的中点 | HY点里程 + 圆曲线 L c L_c Lc的一半 |
| 圆缓点 | YH | 圆曲线与后缓和曲线的连接点 | HY点里程 + 圆曲线长 L c L_c Lc或QZ点里程 + L c 2 \frac{L_c}{2} 2Lc |
| 缓直点 | HZ | 后缓和曲线与直线段的连接点 | YH点里程 + 后缓和曲线长 L s 2 Ls_2 Ls2 |
- 竖曲线
竖曲线用于连接不同纵坡的直线段,通常采用圆曲线形式。其最小半径和最小长度应符合相关规范(有对应的设计规范)。

前坡坡度
i
1
i_1
i1:
i
1
=
H
C
−
H
A
M
i
l
e
a
g
e
C
−
M
i
l
e
a
g
e
A
i_1 = \frac{H_C - H_A}{Mileage_C - Mileage_A}
i1=MileageC−MileageAHC−HA
后坡坡度
i
2
i_2
i2:
i
2
=
H
B
−
H
C
M
i
l
e
a
g
e
B
−
M
i
l
e
a
g
e
C
i_2 = \frac{H_B - H_C}{Mileage_B - Mileage_C}
i2=MileageB−MileageCHB−HC
曲线长
L
L
L:
L
=
R
α
L = R \alpha
L=Rα
坡度差
α
\alpha
α:
α
=
i
1
−
i
2
\alpha = i_1 - i_2
α=i1−i2
切线长
T
T
T:
T
=
L
2
T = \frac{L}{2}
T=2L
外距
E
E
E:
E
=
T
2
2
R
E = \frac{T^2}{2R}
E=2RT2
圆曲线起点A里程值:
M
i
l
e
a
g
e
A
=
M
i
l
e
a
g
e
C
−
T
Mileage_A = Mileage_C - T
MileageA=MileageC−T
圆曲线终点B里程值:
M
i
l
e
a
g
e
B
=
M
i
l
e
a
g
e
C
+
T
Mileage_B = Mileage_C + T
MileageB=MileageC+T
任意点高程计算
竖曲线采用 二次抛物线 设计,方程形式为:
y
=
A
2
L
⋅
x
2
y = \frac{A}{2L} \cdot x^2
y=2LA⋅x2
y
y
y:竖曲线高程修正值(相对于切线高程的变化量)
A
=
i
2
−
i
1
A=i_2−i_1
A=i2−i1:坡度代数差(i1为前坡坡度,i2为后坡坡度)
L
L
L:竖曲线长度
x
x
x:计算点距竖曲线起点(VPC)的水平距离
高程计算步骤:
- 计算切线高程:
H 切线 = H V P C + i 1 ⋅ x H_{切线} = H_{VPC} + i_1 \cdot x H切线=HVPC+i1⋅x - 计算高程修正值
Δ H = A 2 L ⋅ x 2 \Delta H = \frac{A}{2L} \cdot x^2 ΔH=2LA⋅x2 - 实际高程
H = H 切线 + Δ H H = H_{切线} + \Delta H H=H切线+ΔH
有关道路曲线断链的编程
断链的产生原因
断链,指的是因局部改线或分段测量等原因造成的桩号不连续的现象。
地形条件限制:在道路建设过程中,地形条件复杂多变。例如,遇到河流、山谷、山丘等自然障碍物时,道路需要通过曲线来绕开这些障碍。如果道路完全按照直线铺设,可能会导致工程量极大增加,甚至无法施工。设置断链可以合理地调整道路的走向,使道路能够顺应地形,减少对自然环境的破坏,同时降低施工难度和成本。
路线优化需要:从交通流量、行车安全和舒适性等角度考虑,有时需要对道路进行优化。比如在山区道路中,为了保证行车安全,需要设置缓和曲线来降低车辆在转弯时的离心力。通过设置断链,可以将道路划分为不同的线形段落,更好地控制道路的曲率变化,提高道路的使用性能。
断链的类型
分为长链和短链。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








