PRI变换法原理解析及其matlab分析

最新推荐文章于 2023-09-16 16:52:16 发布

请叫我7plus

最新推荐文章于 2023-09-16 16:52:16 发布

阅读量8.1k

点赞数 12

分类专栏：雷达信号处理

本文链接：https://blog.csdn.net/weixin_41544435/article/details/120612244

版权

matlab

雷达信号处理专栏收录该内容

4 篇文章

订阅专栏

---------------------------------------------------------------------------------------------------------------------------------

PRI变换法是雷达信号分选当中的一种经典算法，下面对其原理进行阐述并进行matlab仿真

---------------------------------------------------------------------------------------------------------------------------------

一、PRI变换法原理

1.1、PRI变换法定义

PRI 变换法过程可简单描述为首先对脉冲序列作 PRI 变换处理，然后设置检测门限，如果经 PRI 变换处理得到的 PRI 谱的峰值大于检测门限，则以此峰值对应的 PRI进行序列搜索。

假设信源脉冲流中有 N 个脉冲,到达时间为tn(n=0,1,...N-1), 则截获脉冲表达式如下：

$g(t)=\sum_{n=0}^{N-1}\delta (t-t_n)$

其中， $\delta (t-t_{n})$ 为脉冲到达时间的函数，定义 g(t) 的 PRI 变换公式如下

$D(\tau)=\int g(t)g(t+\tau)e^{j2\pi /\tau}dt,\tau>0$

将g(t) 带入上式子得：

$D(\tau)=\sum_{n=0}^{N-1}\sum_{m=0}^{n-1}\delta (\tau-t_n+t_m)e^{j2\pi/(t_n-t_m)}$

到此为止得到了真正的PRI变换法的公式。

1.2、PRI变换法具体实现

假设检测区间为 $[\tau _{min},\tau _{max}]$ ，将该区间平均分为K个小区间，我们将每个小区间叫做PRI 箱 ( 如下图 ) ，则第个 PRI 箱的中心值可表示为:

$\tau_k=\frac{k-1/2}{K}(\tau_{min}-\tau_{max})+\tau_{min}$ $k=1,2...K$

PRI 变换的谱可表示如下式：

$D_k=\int_{\tau_k-b/2}^{\tau_k+b/2}D(\tau)d\tau=\sum_{\tau_k-b/2<t_n-t_m<\tau+b/2}e^{j2\pi t_n/(t_n-t_m)}$

根据上式，当b趋近于0时 $D_k=D(\tau)$ ，这是在 $D(\tau)$ 连续的时候，但当 $D(\tau)$ 离散的时候如果将每一个箱子宽度表示为1，则 $D_k=D(\tau)$

该步操作是为了更进一步简化运算，如果将每一个箱子宽度表示为1，则 $D_k=D(\tau)$ ,这里的 $D(\tau)$ 是离散形式,如果不这么取的话则一个k的值 $D_k$ 则代表着好几个 $\tau$ 的变换。

算法实现流程图如下：

1.3、相位因子说明

再来说一下相位因子：考虑脉冲 PRI 固定的情况，PRI 箱中序列到达时间 tn 可表示为：

$t_n=(n+\eta )p,n=0,1,...N-1$

则在整个序列中（一个大箱子）

根据上式，由于相位因子的存在，使在 PRI 箱内的具有真实 PRI 值的脉冲数得到

累积，所以在真实 PRI 处会形成谱峰而且很明显。

下面计算一下序列tn的 $l$ 次谐波分量：

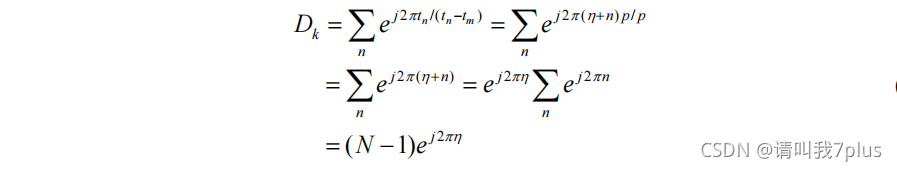
对应脉冲的相位就是

如下图：

可以看出当 $l>=2$ 时，相位之和等于0 ，即可表明自相关出现的子谐波能够被抑制。

1.4、门限说明

计算完PRI谱之后，我们需要设定检测门限来区别出真实 PRI 值所对应的谱峰，

门限设定遵循的原则：观察时间原则，消除子谐波原则以及消除噪声原则

暂不说明。

二、matlab仿真及其结果分析

2.1、单个固定PRI的信号

产出单个固定PRI的信号作为检测到的TOA序列，分别对其进行相关函数变换和PRI变换，运行结果如下：（PRI值为5，第一个TOA为1）

可以看到PRI变化法对谐波的抑制有很好的效果，而且保证不影响实际的PRI值的累计。

2.2、两个固定PRI的信号

这次产生两个固定PRI的信号叠加在一起作为检测序列.

（第一个PRI值为5，TOA为1）

（第二个PRI值为12，TOA为2）

分别对其进行相关函数变换和PRI变换，运行结果如下：

可以看到PRI变化法的优点。

---------------------------------------------------------------------------------------------------------------------------------

附录A 相关函数

假设信源脉冲流中有 N 个脉冲,到达时间为tn(n=0,1,...N-1),则截获脉冲表达式如下：

$g(t)=\sum_{n=0}^{N-1}\delta (t-t_n)$

定义相关函数：

$C(\tau)=\int g(x)g(x+\tau)dt$

将g(t)带入C(\tau)得：

$C(\tau)=\sum_{n=1}^{N-1}\sum_{m=1}^{n-1}\delta (\tau-t_n+t_m)$

---------------------------------------------------------------------------------------------------------------------------------

附录B 推理过程

---------------------------------------------------------------------------------------------------------------------------------

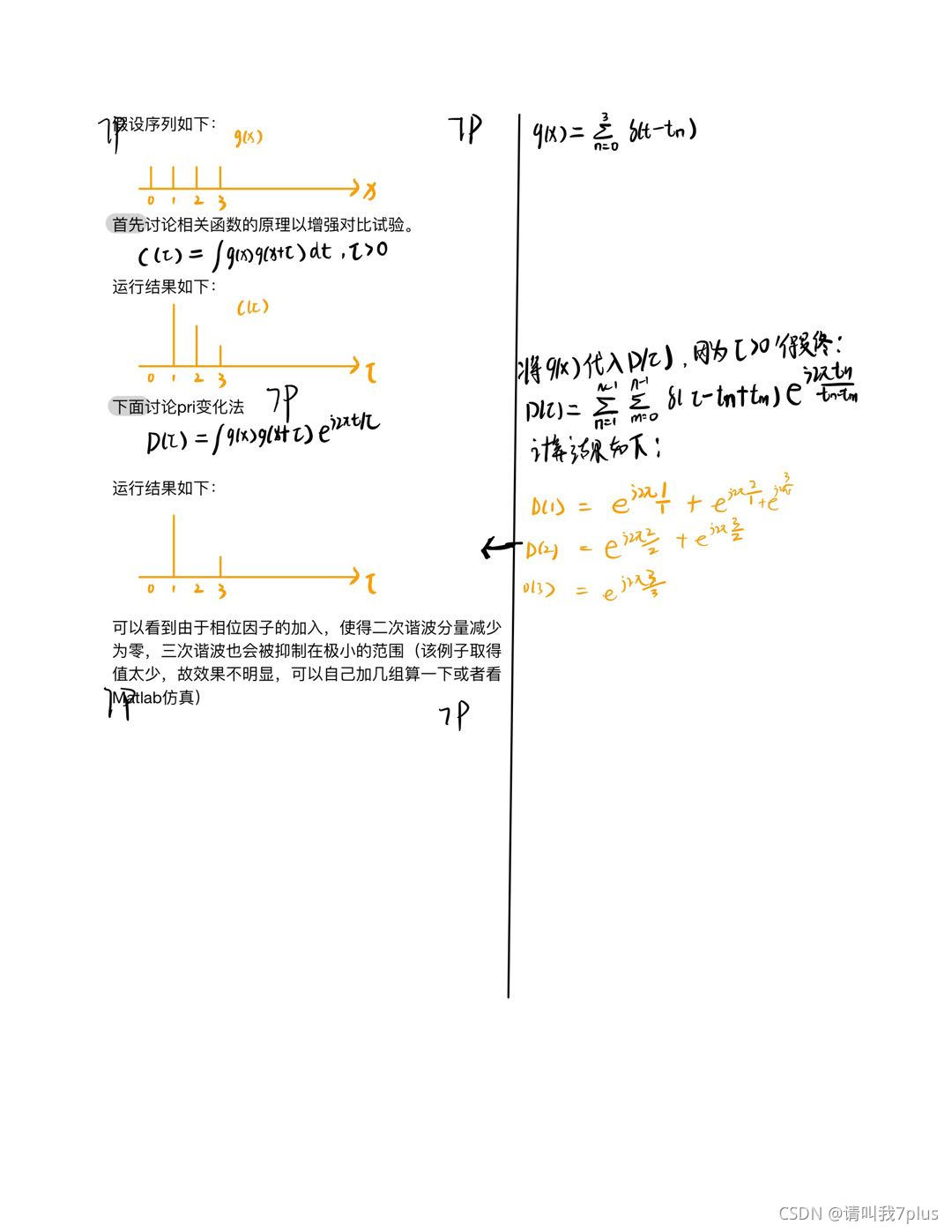
附录C matlab代码：

clear
clc
x_range=50;
x=zeros(1,x_range);
pri_1=5;
pri_2=12;
x(1:pri_1:x_range)=1;%x(1:pri_1:x_range)+1;
x(2:pri_2:x_range)=1;%x(2:pri_3:x_range)+1;
t_n=[];
for p=1:length(x)
    if x(p)~=0
      t_n=cat(2,t_n,p);
    end
end%147852369
diff=[];
for p=1:length(t_n)-1
    diff(p)=t_n(p+1)-t_n(p);%记录tn的值
end
tau_min=min(diff);
tau_max=t_n(length(t_n))-t_n(1);
K=49;
k_bro=1;%手动算一下：k_bro=length[tau_min：tau_max]
D=zeros(1,K);
C=zeros(1,K);
for n=2:length(t_n)
    for m= n-1:-1:1
        tau=t_n(n)-t_n(m);
        if tau < tau_min
            continue
        end
        if tau >= tau_max
            break
        end
        k=ceil(tau/k_bro);
        D(k)=D(k)+exp(1i*2*pi*t_n(m)/tau);
        C(k)=C(k)+1;
    end
end
subplot(131)
stem(x)
subplot(132)
stem(abs(C));
subplot(133)
stem(abs(D));