这里写自定义目录标题
深度学习数学基础
为了帮助读者快速上手深度学习,这里整理其所需要的数学知识的最小集合。掌握这些知识,基本就可以看懂深度学习大部分知识点了。
一、高等数学:导数与偏导数
1. 导数(Derivative)定义

d
y
d
x
=
lim
Δ
x
→
0
Δ
y
Δ
x
\frac{dy}{dx}=\lim_{\Delta x \rightarrow 0}{\frac{\Delta y}{\Delta x}}
dxdy=Δx→0limΔxΔy
或者:
f
′
(
x
0
)
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
f'(x_0)=\lim_{\Delta x \rightarrow 0}{\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}}
f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
常见函数的求导公式如下:
| 原函数 | 导函数 |
|---|---|
| y = c y = c y=c | y ′ = 0 y' = 0 y′=0 |
| y = a x y = a^x y=ax | y ′ = a x ∗ l n ( a ) y' = a^x * ln({a}) y′=ax∗ln(a) |
| y = l o g a ( x ) y = log_a(x) y=loga(x) | y ′ = 1 x ∗ l n ( a ) y' = \frac{1}{x * ln({a})} y′=x∗ln(a)1 |
| y = l n ( x ) y = ln(x) y=ln(x) | y ′ = 1 x y' = \frac{1}{x} y′=x1 |
| y = x n y = x^n y=xn | y ′ = n ∗ x n − 1 y' = n * x^{n-1} y′=n∗xn−1 |
| y = x 1 n y = x^{\frac{1}{n}} y=xn1 | y ′ = 1 n x − n − 1 n y' = \frac{1}{n} x^{-\frac{n-1}{n}} y′=n1x−nn−1 |
| y = s i n ( x ) y = sin(x) y=sin(x) | y ′ = c o s ( x ) y' = cos(x) y′=cos(x) |
| y = c o s ( x ) y = cos(x) y=cos(x) | y ′ = − s i n ( x ) y' = -sin(x) y′=−sin(x) |
| y = t a n ( x ) y = tan(x) y=tan(x) | y ′ = 1 c o s 2 ( x ) = s e c 2 ( x ) y' = \frac{1}{cos^2(x)} = sec^2(x) y′=cos2(x)1=sec2(x) |
| y = c o t ( x ) y = cot(x) y=cot(x) | y ′ = − 1 s i n 2 ( x ) = − c s c 2 ( x ) y' = -\frac{1}{sin^2(x)} = - csc^2(x) y′=−sin2(x)1=−csc2(x) |
| y = s h ( x ) = e x − e − x 2 y = sh(x) = \frac{e^x - e^{-x}}{2} y=sh(x)=2ex−e−x | y ′ = c h ( x ) y' = ch(x) y′=ch(x) |
| y = c h ( x ) = e x + e − x 2 y = ch(x) = \frac{e^x + e^{-x}}{2} y=ch(x)=2ex+e−x | y ′ = s h ( x ) y' = sh(x) y′=sh(x) |
| y = t h ( x ) = e x − e − x e x + e − x y = th(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} y=th(x)=ex+e−xex−e−x | y ′ = 1 c h 2 ( x ) y' = \frac{1}{ch^2(x)} y′=ch2(x)1 |
2. 偏导数
一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
偏导数的极限定义:
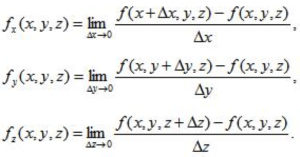
根据偏导数定义可知,表1的导数公式同样适用于偏导数。
3. 链式求导法则
链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。复合函数的导数将是构成复合这有限个函数在相应点的 导数的乘积,就像锁链一样一环套一环,故称链式法则。详见百度百科: 链式法则
简单讲,若:
z
=
g
(
y
)
z = g(y)
z=g(y)
y
=
g
(
x
)
y = g(x)
y=g(x)
则有:
d
z
d
x
=
d
z
d
y
∗
d
y
d
x
\frac{dz}{dx} = \frac{dz}{dy} * \frac{dy}{dx}
dxdz=dydz∗dxdy
二、矩阵
1. 矩阵的定义:
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
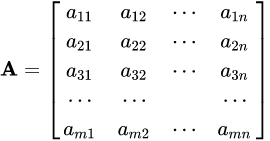
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
2. 基本运算
2.1 加法
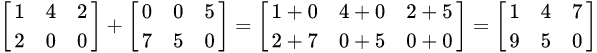
矩阵的加法满足下列运算律(A,B,C都是同型矩阵):
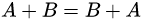
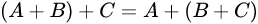
应该注意的是只有同型矩阵之间才可以进行加法
2.2 减法
示例:
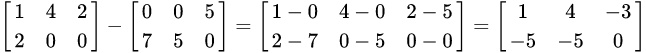
2.3 数乘
示例:
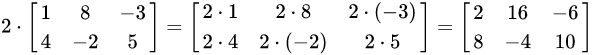
矩阵的数乘满足以下运算律:
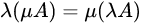
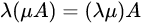
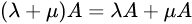
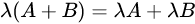
矩阵的加减法和矩阵的数乘合称矩阵的线性运算
2.4 转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵(
A
T
A^T
AT),这一过程称为矩阵的转置:
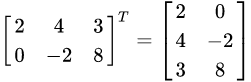
矩阵的转置满足以下运算律:
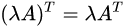
3. 乘法
3.1 定义:
设A为
m
×
p
m \times p
m×p的矩阵,B为
p
×
n
p \times n
p×n的矩阵,那么称
m
×
n
m \times n
m×n的矩阵C为矩阵A与B的乘积,记作
C
=
A
B
C=AB
C=AB,其中矩阵C中的第 i 行第 j 列元素可以表示为:
(
A
B
)
i
j
=
∑
k
=
1
p
a
i
k
b
k
j
=
a
i
1
b
1
j
+
a
i
2
b
2
j
+
.
.
.
+
a
i
p
b
p
j
(AB)_{ij}=\sum_{k=1}^p{a_{ik}}b_{kj} = a_{i1}b_{1j} + a_{i2}b_{2j} + ... + a_{ip}b_{pj}
(AB)ij=k=1∑paikbkj=ai1b1j+ai2b2j+...+aipbpj
如下所示:
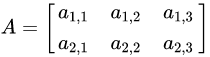
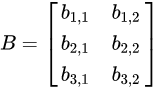
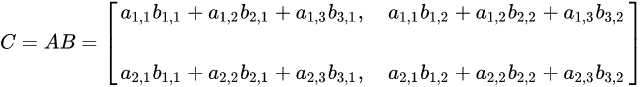
3.2 注意事项
- 当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
- 矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
- 乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
3.3 基本性质
- 乘法结合律: (AB)C=A(BC). [3]
- 乘法左分配律:(A+B)C=AC+BC [3]
- 乘法右分配律:C(A+B)=CA+CB [3]
- 对数乘的结合性k(AB)=(kA)B=A(kB).
- 转置 (AB)T=BTAT.
- 矩阵乘法在以下两种情况下满足交换律。
- AA*=A*A,A和伴随矩阵相乘满足交换律。
- AE=EA,A和单位矩阵或数量矩阵满足交换律。
三、向量
1. 向量的定义
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
向量的代数表示
一般印刷用黑体的小写英文字母(a、b、c等)来表示,手写用在a、b、c等字母上加一箭头(→)表示,如 ,也可以用大写字母AB、CD上加一箭头(→)等表示。
- 二维向量:v = (x1, x2)
- 三维向量:v = (x1, x2, x3)
- n维向量:v = (x1, x2, …, xn)
向量的几何表示
向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。长度为0的向量叫做零向量,记作长度等于1个单位的向量,叫做单位向量。

向量的矩阵表示
向量也可以表示为矩阵形式:
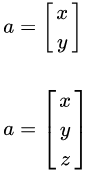
2 向量的运算
2.2.1 向量的加法:
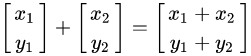
加法的几何意义:

2.2 向量的点积
点积在数学中,又称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
点积有两种定义方式:代数方式和几何方式。
-
代数定义:两个n维向量a和b的点积定义为:
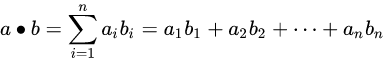
a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . + a n b n a \cdot b = \sum_{i=1}^{n}{a_ib_i} = a_1b_1 + a_2b_2 + ... + a_nb_n a⋅b=i=1∑naibi=a1b1+a2b2+...+anbn -
几何定义:设二维空间内有两个向量 a ⃗ \vec{a} a和 b ⃗ \vec{b} b,和表示向量a和b的大小,它们的夹角为 θ \theta θ,则内积定义为以下实数:
a ⃗ ⋅ b ⃗ = ∣ a ∣ ∣ b ∣ c o s θ \vec{a} \cdot \vec{b} = |a||b|cos\theta a⋅b=∣a∣∣b∣cosθ
3. 向量的距离
向量的距离通常有两种度量方式:欧式距离 和 向量夹角。机器学习中比较常用的是利用向量夹角度量两个向量的距离(相似性)
3.1 欧式距离:
欧式距离,即向量作为两个点的空间直线距离。
若:
a
⃗
=
(
a
1
,
a
2
,
a
3
)
\vec{a} = (a_1,a_2,a_3)
a=(a1,a2,a3)
b
⃗
=
(
b
1
,
b
2
,
b
3
)
\vec{b} = (b_1,b_2,b_3)
b=(b1,b2,b3)
则欧式距离计算公式为:
∣
a
⃗
−
b
⃗
∣
=
(
a
1
−
b
1
)
2
+
(
a
2
−
b
2
)
+
(
a
3
−
b
3
)
|\vec{a} - \vec{b}| = \sqrt{(a_1 - b_1)^2+(a_2 - b_2)+(a_3 - b_3)}
∣a−b∣=(a1−b1)2+(a2−b2)+(a3−b3)
3.2 向量夹角:
若:
a
⃗
=
(
a
1
,
a
2
,
a
3
)
\vec{a} = (a_1,a_2,a_3)
a=(a1,a2,a3)
b
⃗
=
(
b
1
,
b
2
,
b
3
)
\vec{b} = (b_1,b_2,b_3)
b=(b1,b2,b3)
则夹角计算公式为:
c
o
s
<
a
⃗
,
b
⃗
>
=
a
⃗
⋅
⃗
b
∣
a
⃗
∣
∣
b
⃗
∣
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
a
1
2
+
a
2
2
+
a
3
2
b
1
2
+
b
2
2
+
b
3
2
cos<\vec{a},\vec{b}> = \frac{\vec{a} \cdot \vec{}b}{|\vec{a}||\vec{b}|} = \frac{a_1b_1 + a_2b_2 + a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}
cos<a,b>=∣a∣∣b∣a⋅b=a12+a22+a32b12+b22+b32a1b1+a2b2+a3b3
四、概率论与数理统计
1. 概率论基本概念
随机实验(E)
- (1)可以在相同的条件下重复地进行
- (2)每次实验的可能结果不止一个,并且事先明确知道实验的所有可能结果
- (3)每次试验将出现哪一个结果无法预知
例子:抛一枚硬币,观察正面,反面出现的情况
样本空间 (Ω)
随机试验所有可能的结果组成的集合
-
样本点
样本空间的元素,即每个可能的结果 -
随机事件
随机试验E的样本空间S的子集称为随机事件 -
基本事件
样本空间的单个元素,一个可能结果构成的集合 -
必然事件(全集)、不可能事件(空集)
事件的关系与事件的运算 (类似于集合运算)
包含关系、和(并)并事件、积(交)事件、差事件、互不相容(互斥)、逆事件(对立事件)


2. 运算规律

- 常用结论:
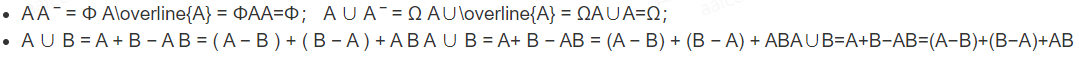
3. 重要公式及结论
-
条件概率
条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为:P(A|B),读作“在B的条件下A的概率”:
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB) -
贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) ∗ P ( A ) / P ( B ) P(A|B)=P(B|A)*P(A)/P(B) P(A∣B)=P(B∣A)∗P(A)/P(B)

-
全概率公式
P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) = P ( A ∣ B 1 ) P ( B 1 ) + P ( A ∣ B 2 ) P ( B 2 ) + . . . + P ( A ∣ B n ) P ( B n ) P(A) = \sum_{i=1}^{n}{P(B_i)P(A|B_i)} = P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + ... + P(A|B_n)P(B_n) P(A)=i=1∑nP(Bi)P(A∣Bi)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)
4. 随机变量的数字特征
- 数学期望
P X = x i = p i P{X=x_i} = p_i PX=xi=pi E ( X ) = ∑ i x i p i E(X) = \sum_i{x_ip_i} E(X)=i∑xipi - 方差
D ( X ) = E [ X − E ( X ) ] 2 = E ( X 2 ) − [ E ( X ) ] 2 D(X)=E[X-E(X)]^2=E(X^2)-[E(X)]^2 D(X)=E[X−E(X)]2=E(X2)−[E(X)]2





















 664
664











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








