使用Python从0开始搭建神经网络

创建你自己的机器学习库

在这篇文章中，我们将从头开始学习机器学习的数学原理，并使用 Python 编写代码，来构建具有各种层（全连接、卷积等）的神经网络。最终，我们将能够以模块化方式创建网络：

层与层

我们需要牢记这里的基本架构：

1. 我们将输入数据输入神经网络。
2. 数据从一层流到另一层，直到我们得到输出。
3. 一旦我们有了输出，我们就可以计算误差，它是一个标量。
4. 最后，我们可以通过减去误差相对于参数本身的导数来调整给定的参数（权重或偏差） 。
5. 迭代这个过程。

最重要的一步是第四步。我们希望能够拥有任意数量的任意类型的层。但是，如果我们修改/添加/删除网络中的一层，网络的输出将会改变，这将改变误差，这将改变误差相对于参数的导数。无论网络架构如何，无论激活函数如何，无论我们使用的损失如何，我们都需要能够计算导数。

为了实现这一点，我们必须单独实现每一层。

每层应该实现什么

我们可能创建的每一层（全连接层、卷积层、最大池化层、dropout 层等）至少有两个共同点：输入和输出数据。

前向传播
我们已经可以强调一个重要的一点：一层的输出是下一层的输入。

这称为前向传播。本质上，我们将输入数据提供给第一层，然后每一层的输出成为下一层的输入，直到到达网络的末端。通过将网络结果 (Y) 与所需输出（假设为 Y*）进行比较，我们可以计算误差E。目标是通过更改网络中的参数来最小化该错误。这就是反向传播 （backpropagation）

梯度下降
（这块的网络资料很多，大家可以随意参考）

我们想要改变网络中的一些参数（称为w），以便总误差E 减少。有一种巧妙的方法（不是随机的），如下所示：
$$w\leftarrow w-\alpha \frac{\partial E}{\partial w}$$

其中α是我们设置的[0,1]范围内的参数，称为学习率。梯度下降通过计算函数的梯度（即函数在各个参数上的导数），然后朝着梯度的反方向调整参数，因为这个方向是减少函数值的最快路径。通过反复迭代这个过程，梯度下降法能够使得函数走向局部最小值，从而优化模型的性能。无论如何，这里重要的是∂E/∂w（E 对 w 的导数）。我们需要找到网络中每个参数的表达式的值。

向后传播
在神经网络中，每一层都需要根据接收到的输出误差的变化率（导数）来计算输入误差的变化率。想象每一层都是一个工厂：这个工厂收到了一些产品（输出Y），并且得知了这批产品的质量问题（误差E）对销售的影响（即误差相对于输出的导数，∂E/∂Y）。为了找出是哪个原料（输入X）造成了问题，工厂就需要追踪并计算这些问题是如何从原料传递到产品的，即它需要确定原料的哪些问题（误差相对于输入的导数，∂E/∂X）导致了最终产品的质量问题。这样，工厂就能调整原料的使用或处理方式，来减少未来产品的缺陷。

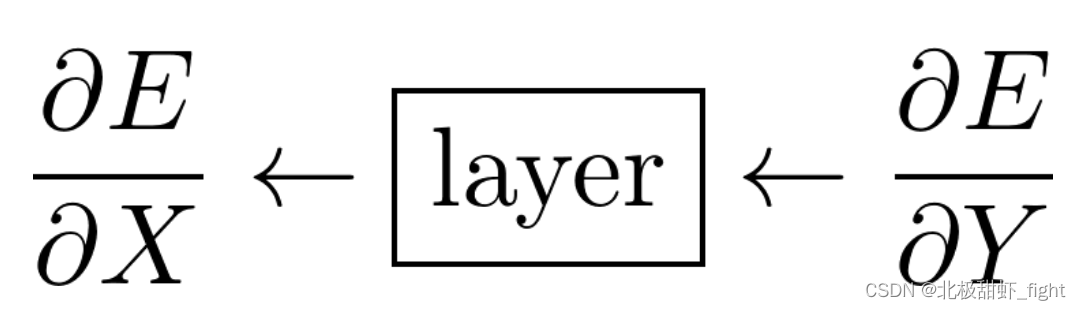
请记住，E是标量（数字） ，X和Y是矩阵
$$\begin{array}{rl}& \frac{\partial E}{\partial X}=\left[\begin{array}{llll}\frac{\partial E}{\partial x_1}& \frac{\partial E}{\partial x_2}& \dots & \frac{\partial E}{\partial x_i}\end{array}\right]\\ & \frac{\partial E}{\partial Y}=\left[\begin{array}{llll}\frac{\partial E}{\partial y_1}& \frac{\partial E}{\partial y_2}& \dots & \frac{\partial E}{\partial y_j}\end{array}\right]\end{array}$$
现在让我们不用管 ∂E/∂X。这里的技巧是，如果我们能够得到 ∂E/∂Y，我们就可以非常轻松地计算 ∂E/∂W（如果该层有可训练参数），而无需了解任何除了这层之外的网络架构信息！我们简单地使用链式法则：
$$\begin{array}{r}\frac{\partial E}{\partial w}=\sum _j\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial w}\end{array}$$
未知数是∂y_j/∂w，这完全取决于该层如何计算其输出。因此，如果每个层都可以访问 ∂E/∂Y，其中 Y 是其自己的输出，那么我们就可以更新我们的参数！

这样说可能有些抽象，我们举个简单的toy case来说明这件事：

理解反向传播的图表

第 3 层将使用 ∂E/∂Y 更新其参数，然后将 ∂E/∂H2 传递到前一层，即其自己的“∂E/∂Y”。然后，第 2 层将执行相同的操作，依此类推。

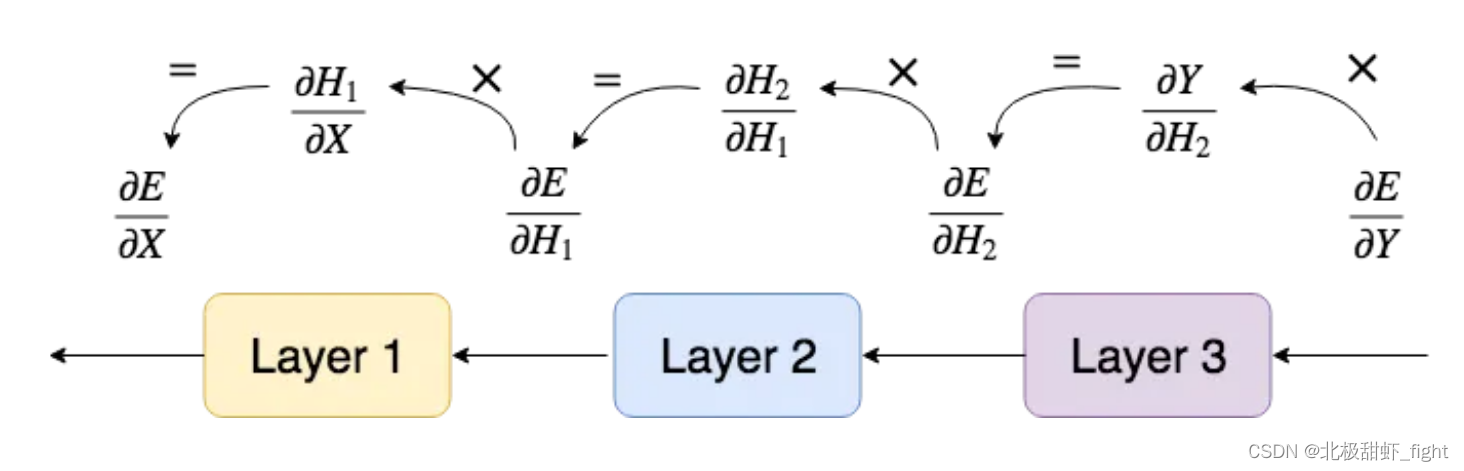
下面我们通过代码进一步具象化

抽象基类：layer
所有其他层都将从抽象类Layer继承，它处理简单的属性，即输入、输出以及前向和后向方法

# Base class
class Layer:
    def __init__(self):
        self.input = None
        self.output = None

    # computes the output Y of a layer for a given input X
    def forward_propagation(self, input):
        raise NotImplementedError

    # computes dE/dX for a given dE/dY (and update parameters if any)
    def backward_propagation(self, output_error, learning_rate):
        raise NotImplementedError

这里backward_propagation有一个没有提到的额外参数，它是learning_rate.这个参数类似于更新策略，或者是 Keras 中所说的优化器，但为了简单起见，我们只是传递一个学习率并使用梯度下降来更新我们的参数。

全连接层
现在让我们定义并实现第一种类型的层：全连接层或FC层。 FC 层是最基本的层，因为每个输入神经元都连接到每个输出神经元。

前向传播
每个输出神经元的值可以计算如下：
$$\begin{array}{r}{y}_j=b_j+\sum _i{x}_i{w}_{ij}\end{array}$$
通过矩阵，我们可以使用点积一次计算每个输出神经元的公式:

我们已经完成了前向传播。现在让我们进行FC层的向后传递

---

请注意，目前还没有使用任何激活函数，我们将在单独的层中实现它

---

向后传播
我们需要 ：

1. 误差相对于参数 (∂E/∂W, ∂E/∂B) 的导数
2. 误差相对于输入的导数 (∂E/∂X)

我们来计算 ∂E/∂W。该矩阵应与 W 本身大小相同：ixj 其中 i 是输入神经元的数量和 j 输出神经元的数量。我们需要为每个权重提供一个梯度：

使用前面提到的链式法则，我们可以写
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial w_{ij}}\end{array}& \begin{array}{r}=\frac{\partial E}{\partial y_1}\frac{\partial y_1}{\partial w_{ij}}+\dots +\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial w_{ij}}\end{array}\\ & =\frac{\partial E}{\partial y_j}{x}_i\end{array}$$
所以，
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial W}\end{array}& =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}{x}_1& \dots & \frac{\partial E}{\partial y_j}{x}_1\\ ⋮& \ddots & ⋮\\ \frac{\partial E}{\partial y_1}{x}_i& \dots & \frac{\partial E}{\partial y_j}{x}_i\end{array}\right]\\ & =\left[\begin{array}{c}{x}_1\\ ⋮\\ x_i\end{array}\right]\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}& \dots & \frac{\partial E}{\partial y_j}\end{array}\right]\\ & \begin{array}{r}=X^t\frac{\partial E}{\partial Y}\end{array}\end{array}$$
这就是我们第一个更新权重的公式！现在我们来计算 ∂E/∂B
$$\frac{\partial E}{\partial B}=\left[\begin{array}{cccc}\frac{\partial E}{\partial b_1}& \frac{\partial E}{\partial b_2}& \dots & \frac{\partial E}{\partial b_j}\end{array}\right]$$
同样，∂E/∂B 需要与 B 本身具有相同的大小，每个偏置项都会有一个梯度。我们可以再次使用链式法则
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial b_j}\end{array}& \begin{array}{r}=\frac{\partial E}{\partial y_1}\frac{\partial y_1}{\partial b_j}+\dots +\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial b_j}\end{array}\\ & =\frac{\partial E}{\partial y_j}\end{array}$$
并得出结论
$$\begin{array}{rl}\frac{\partial E}{\partial B}& =\left[\begin{array}{cccc}\frac{\partial E}{\partial y_1}& \frac{\partial E}{\partial y_2}& \dots & \frac{\partial E}{\partial y_j}\end{array}\right]\\ & =\frac{\partial E}{\partial Y}\end{array}$$
现在我们有了∂E/∂W和∂E/∂B， 剩下了∂E/∂X，这非常重要，因为它将“充当”该层之前的层的 ∂E/∂Y
$$\frac{\partial E}{\partial X}=\left[\begin{array}{cccc}\frac{\partial E}{\partial x_1}& \frac{\partial E}{\partial x_2}& \dots & \frac{\partial E}{\partial x_i}\end{array}\right]$$
再次，使用链式法则
$$\begin{array}{c}\begin{array}{r}\frac{\partial E}{\partial x_i}\end{array}\begin{array}{r}=\frac{\partial E}{\partial y_1}\frac{\partial y_1}{\partial x_i}+\dots +\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial x_i}\end{array}\\ =\frac{\partial E}{\partial y_1}{w}_{i1}+\dots +\frac{\partial E}{\partial y_j}{w}_{ij}\end{array}$$
最后，我们可以写出整个矩阵
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial X}\end{array}& =\left[\begin{array}{ccc}(\frac{\partial E}{\partial y_1}{w}_{11}+\dots +\frac{\partial E}{\partial y_j}{w}_{1j})& \dots & (\frac{\partial E}{\partial y_1}{w}_{i1}+\dots +\frac{\partial E}{\partial y_j}{w}_{ij})\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}& \dots & \frac{\partial E}{\partial y_j}\end{array}\right]\left[\begin{array}{ccc}{w}_{11}& \dots & w_{i1}\\ ⋮& \ddots & ⋮\\ w_{1j}& \dots & w_{ij}\end{array}\right]\\ & =\frac{\partial E}{\partial Y}{W}^t\end{array}$$
就是这样！我们有了 FC 层所需的三个公式！

$$\begin{array}{rl}& \begin{array}{r}\frac{\partial E}{\partial X}=\frac{\partial E}{\partial Y}{W}^t\end{array}\\ & \begin{array}{r}\frac{\partial E}{\partial W}=X^t\frac{\partial E}{\partial Y}\end{array}\\ & \begin{array}{r}\frac{\partial E}{\partial B}=\frac{\partial E}{\partial Y}\end{array}\end{array}$$

编码全连接层
我们现在可以编写一些 Python 代码来将这个数学表达变为现实！

from layer import Layer
import numpy as np

# inherit from base class Layer
class FCLayer(Layer):
    # input_size = number of input neurons
    # output_size = number of output neurons
    def __init__(self, input_size, output_size):
        self.weights = np.random.rand(input_size, output_size) - 0.5
        self.bias = np.random.rand(1, output_size) - 0.5

    # returns output for a given input
    def forward_propagation(self, input_data):
        self.input = input_data
        self.output = np.dot(self.input, self.weights) + self.bias
        return self.output

    # computes dE/dW, dE/dB for a given output_error=dE/dY. Returns input_error=dE/dX.
    def backward_propagation(self, output_error, learning_rate):
        input_error = np.dot(output_error, self.weights.T)
        weights_error = np.dot(self.input.T, output_error)
        # dBias = output_error

        # update parameters
        self.weights -= learning_rate * weights_error
        self.bias -= learning_rate * output_error
        return input_error

激活层

到目前为止我们所做的所有计算都是完全线性的。用这种模型无法用来学习任何东西。我们需要通过将非线性函数应用于某些层的输出来向模型添加非线性。

现在我们需要为神经网络层重做整个过程！

由于没有可学习的参数，它会更快。我们只需要计算∂E/∂X

我们将分别调用f和f’激活函数及其导数

前向传播

这步非常简单。对于给定的输入X，输出只是应用于 的每个元素的激活函数X。这意味着输入和输出具有相同的维度。
$$\begin{array}{rl}Y& =\left[\begin{array}{ccc}f(x_1)& \dots & f(x_i)\end{array}\right]\\ & =f(X)\end{array}$$
向后传播

给定∂E/∂Y，我们要计算∂E/∂X
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial X}\end{array}& =\left[\begin{array}{ccc}\frac{\partial E}{\partial x_1}& \dots & \frac{\partial E}{\partial x_i}\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}\frac{\partial y_1}{\partial x_1}& \dots & \frac{\partial E}{\partial y_i}\frac{\partial y_i}{\partial x_i}\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}{f}^{\prime }(x_1)& \dots & \frac{\partial E}{\partial y_i}{f}^{\prime }(x_i)\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}& \dots & \frac{\partial E}{\partial y_i}\end{array}\right]\odot \left[\begin{array}{ccc}{f}^{\prime }(x_1)& \dots & f^{\prime }(x_i)\end{array}\right]\\ & =\frac{\partial E}{\partial Y}\odot f^{\prime }(X)\end{array}$$
这里我们在两个矩阵之间使用逐元素乘法（而在上面的公式中，它是点积）

编写激活层

from layer import Layer

# inherit from base class Layer
class ActivationLayer(Layer):
    def __init__(self, activation, activation_prime):
        self.activation = activation
        self.activation_prime = activation_prime

    # returns the activated input
    def forward_propagation(self, input_data):
        self.input = input_data
        self.output = self.activation(self.input)
        return self.output

    # Returns input_error=dE/dX for a given output_error=dE/dY.
    # learning_rate is not used because there is no "learnable" parameters.
    def backward_propagation(self, output_error, learning_rate):
        return self.activation_prime(self.input) * output_error

还可以在单​​独的文件中编写一些激活函数及其派生函数。稍后将使用这些来创建ActivationLayer

import numpy as np

# activation function and its derivative
def tanh(x):
    return np.tanh(x);

def tanh_prime(x):
    return 1-np.tanh(x)**2;

损失函数

到目前为止，对于给定的层，我们假设∂E/∂Y是 给定的（由下一层）。但是最后一层会发生什么呢？如何得到∂E/∂Y？我们只是手动给出，这取决于我们如何定义错误。

网络的误差由你自行定义，它衡量网络对于给定输入数据的表现有多好或多坏。定义误差的方法有很多种，其中最著名的一种称为MSE——均方误差。
$$\begin{array}{r}E=\frac{1}{n}\sum _i^n(y_i^{\ast }-y_i{)}^2\end{array}$$
其中y*和分别y表示期望输出和实际输出。可以将损失视为最后一层，它将所有输出神经元压缩为一个神经元。与其他所有层一样，我们现在需要的是定义∂E/∂Y。但现在，我们终于到达了E！
$$\begin{array}{rl}\begin{array}{r}\frac{\partial E}{\partial Y}\end{array}& =\left[\begin{array}{ccc}\frac{\partial E}{\partial y_1}& \dots & \frac{\partial E}{\partial y_i}\end{array}\right]\\ & =\frac{2}{n}\left[\begin{array}{ccc}{y}_1-y_1^{\ast }& \dots & y_i-y_i^{\ast }\end{array}\right]\\ & =\frac{2}{n}(Y-Y^{\ast })\end{array}$$
这些只是两个 python 函数，可以将它们放在单独的文件中。创建网络时将使用它们

import numpy as np

# loss function and its derivative
def mse(y_true, y_pred):
    return np.mean(np.power(y_true-y_pred, 2));

def mse_prime(y_true, y_pred):
    return 2*(y_pred-y_true)/y_true.size;

网络类

快完成了！我们将创建一个Network类来非常容易地创建神经网络，类似于开头第一张图片

class Network:
    def __init__(self):
        self.layers = []
        self.loss = None
        self.loss_prime = None

    # add layer to network
    def add(self, layer):
        self.layers.append(layer)

    # set loss to use
    def use(self, loss, loss_prime):
        self.loss = loss
        self.loss_prime = loss_prime

    # predict output for given input
    def predict(self, input_data):
        # sample dimension first
        samples = len(input_data)
        result = []

        # run network over all samples
        for i in range(samples):
            # forward propagation
            output = input_data[i]
            for layer in self.layers:
                output = layer.forward_propagation(output)
            result.append(output)

        return result

    # train the network
    def fit(self, x_train, y_train, epochs, learning_rate):
        # sample dimension first
        samples = len(x_train)

        # training loop
        for i in range(epochs):
            err = 0
            for j in range(samples):
                # forward propagation
                output = x_train[j]
                for layer in self.layers:
                    output = layer.forward_propagation(output)

                # compute loss (for display purpose only)
                err += self.loss(y_train[j], output)

                # backward propagation
                error = self.loss_prime(y_train[j], output)
                for layer in reversed(self.layers):
                    error = layer.backward_propagation(error, learning_rate)

            # calculate average error on all samples
            err /= samples
            print('epoch %d/%d   error=%f' % (i+1, epochs, err))

构建神经网络

我们可以使用我们的类来创建一个具有任意层数的神经网络！我们将构建两个神经网络：一个简单的XOR和一个MNIST求解器

解决异或
从 XOR 开始始终很重要，因为它是判断网络是否正在学习任何内容的简单方法。

import numpy as np

from network import Network
from fc_layer import FCLayer
from activation_layer import ActivationLayer
from activations import tanh, tanh_prime
from losses import mse, mse_prime

# training data
x_train = np.array([[[0,0]], [[0,1]], [[1,0]], [[1,1]]])
y_train = np.array([[[0]], [[1]], [[1]], [[0]]])

# network
net = Network()
net.add(FCLayer(2, 3))
net.add(ActivationLayer(tanh, tanh_prime))
net.add(FCLayer(3, 1))
net.add(ActivationLayer(tanh, tanh_prime))

# train
net.use(mse, mse_prime)
net.fit(x_train, y_train, epochs=1000, learning_rate=0.1)

# test
out = net.predict(x_train)
print(out)

这里的输入样本维度是(4,1,2)

结果

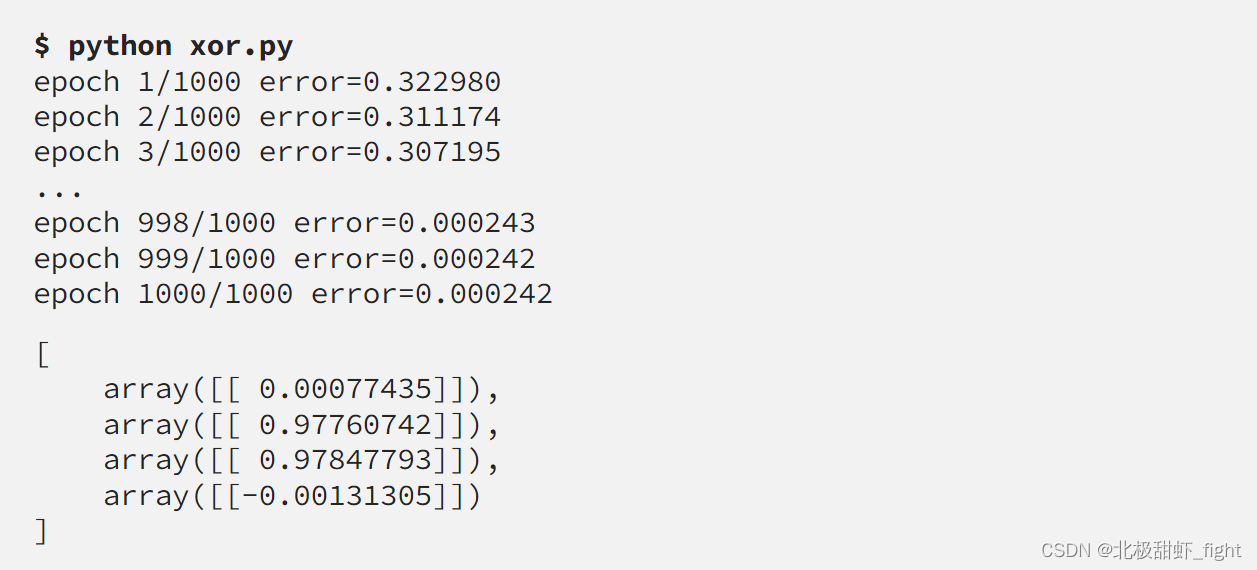
符合我们的预期！

解决 MNIST

我们没有实现卷积层，但这不是问题。我们需要做的就是重塑数据，使其适合全连接层。

MNIST 数据集由 0 到 9 的数字图像组成，形状为 28x28x1。目标是预测图片上绘制的数字。

import numpy as np

from network import Network
from fc_layer import FCLayer
from activation_layer import ActivationLayer
from activations import tanh, tanh_prime
from losses import mse, mse_prime

from keras.datasets import mnist
from keras.utils import np_utils

# load MNIST from server
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# training data : 60000 samples
# reshape and normalize input data
x_train = x_train.reshape(x_train.shape[0], 1, 28*28)
x_train = x_train.astype('float32')
x_train /= 255
# encode output which is a number in range [0,9] into a vector of size 10
# e.g. number 3 will become [0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
y_train = np_utils.to_categorical(y_train)

# same for test data : 10000 samples
x_test = x_test.reshape(x_test.shape[0], 1, 28*28)
x_test = x_test.astype('float32')
x_test /= 255
y_test = np_utils.to_categorical(y_test)

# Network
net = Network()
net.add(FCLayer(28*28, 100))                # input_shape=(1, 28*28)    ;   output_shape=(1, 100)
net.add(ActivationLayer(tanh, tanh_prime))
net.add(FCLayer(100, 50))                   # input_shape=(1, 100)      ;   output_shape=(1, 50)
net.add(ActivationLayer(tanh, tanh_prime))
net.add(FCLayer(50, 10))                    # input_shape=(1, 50)       ;   output_shape=(1, 10)
net.add(ActivationLayer(tanh, tanh_prime))

# train on 1000 samples
# as we didn't implemented mini-batch GD, training will be pretty slow if we update at each iteration on 60000 samples...
net.use(mse, mse_prime)
net.fit(x_train[0:1000], y_train[0:1000], epochs=35, learning_rate=0.1)

# test on 3 samples
out = net.predict(x_test[0:3])
print("\n")
print("predicted values : ")
print(out, end="\n")
print("true values : ")
print(y_test[0:3])

结果

Perfect！！！

感谢各位阅读~ 如果有所收获，欢迎关注。 您的支持是我创作的最大动力