测试算法有效性：显著性分析

最新推荐文章于 2023-12-01 17:27:32 发布

weixin_42001089

最新推荐文章于 2023-12-01 17:27:32 发布

阅读量5.1k

点赞数 5

分类专栏：算法文章标签：显著性 delta method

本文链接：https://blog.csdn.net/weixin_42001089/article/details/117188922

版权

算法专栏收录该内容

56 篇文章 2 订阅

订阅专栏

前言

今天偶尔刷到一篇博客如下，里面涉及到了很多数学小知识点，基本都是很实用的数学常识，不论从事什么领域，其实都很有帮助，为此记录一下吧。

十分钟读懂Delta Method在AB测试中的应用

下面分多个大标题，记录一下各个使用的点【下面多张图片均来源于以上博客】

显著性分析

这是非常重要了，可以参考

关于显著性检验，你想要的都在这儿了！！（基础篇）_championkai的博客-CSDN博客_显著性差异

基本上我们要分析两个变量或多个变量之间的差异有多大，就会用到显著性分析，而该场景可以说太多了，所以学好显著性分析非常有用，之间在大学和考研期间学过一些皮毛，脑海中能记得就是一堆假设检验，不过一般的话我们只需要使用这些简单的就够了

delta method

我们知道一个随机变量X的方差var(X)，那么经过线性变化Y=ax+b 后，Y的方差也是知道的： $a^{2}$ *var(X), 但如果不是线性变化呢即泛化成 f(X)？delta method就是解决这一类问题的,大概思路就是如果我们将f(X)转化成一个线性变化，而这个线性变化是逼近f(X)，那不就行了，即该线性变化又能代表f(X)，又能直接利用 $a^{2}$ *var(X)得到新构建随机变量Y的方差，所以问题转变为怎么求得f(X)的近似线性函数，delta method基于的是泰勒展开式，用近似的方法估计随机变量函数的方差。

复杂的变化，可以查看更多文献，但简单概括来说其解决了如下问题：

$Y = f(X) \\ D(Y) = ({f(X)}')^{2}D(X)$

即

这是一元的（一个随机变量），如果是多元的

下面我们通过一个例子来详细看看delta method的具体计算过程即博客中的一个例子推导：

博客中直接给出了结果，那么详细过程是什么呢？其实如下：

$var(\frac{\overline{X}}{\overline{Y}})=\begin{pmatrix} \frac{\partial g(\mu_{x},\mu_{y}))}{\partial \mu_{x}}& \frac{\partial g(\mu_{x},\mu_{y}))}{\partial \mu_{y}} \end{pmatrix}\begin{pmatrix} var(\overline{X}) & COV(\overline{X},\overline{Y}))\\ COV(\overline{Y},\overline{X})) & var(\overline{Y}) \end{pmatrix}\begin{pmatrix} \frac{\partial g(\mu_{x},\mu_{y}))}{\partial \mu_{x}}& \frac{\partial g(\mu_{x},\mu_{y}))}{\partial \mu_{y}} \end{pmatrix}^{T}\\= \begin{pmatrix} \frac{1}{\mu_{y}} & -\frac{\mu_{x}}{\mu_{y}^{2}} \end{pmatrix}\begin{pmatrix} var(\overline{X}) & COV(\overline{X},\overline{Y}))\\ COV(\overline{Y},\overline{X})) & var(\overline{Y}) \end{pmatrix}\begin{pmatrix} \frac{1}{\mu_{y}} & -\frac{\mu_{x}}{\mu_{y}^{2}} \end{pmatrix}^{T}$

$=\begin{pmatrix} \frac{var(\overline{X})}{\mu_{y}} -\frac{\mu_{x}COV(\overline{X},\overline{Y})}{\mu_{y}^{2}}& \frac{COV(\overline{X},\overline{Y})}{\mu_{y}}-\frac{\mu_{x}var(\overline{Y})}{\mu_{y}^{2}} \end{pmatrix}\begin{pmatrix} \frac{1}{\mu_{y}} & -\frac{\mu_{x}}{\mu_{y}^{2}} \end{pmatrix}^{T}$

$=\frac{var(\overline{X})}{\mu _{y}^{2}}-\frac{\mu_{x}COV(\overline{X},\overline{Y})}{\mu _{y}^{3}}-\frac{\mu _{x}COV(\overline{X},\overline{Y})}{\mu _{y}^{3}}+\frac{\mu _{x}^{2}var(\overline{Y})}{\mu _{y}^{4}}$

$=\frac{var(\overline{X})}{\mu _{y}^{2}}+\frac{\mu _{x}^{2}var(\overline{Y})}{\mu _{y}^{4}}-\frac{2\mu_{x}COV(\overline{X},\overline{Y})}{\mu _{y}^{3}}$

$=\frac{var(\overline{X})}{{\overline{Y}}^{2}}+\frac{\overline{X}^{2}var(\overline{Y})}{\overline{Y}^{4}}-2\frac{\overline{X}COV(\overline{X},\overline{Y})}{\overline{Y}^{3}}{\color{Red} (1)}$

$=\frac{var(\frac{X}{n})}{{\overline{Y}}^{2}}+\frac{\overline{X}^{2}var(\frac{Y}{n})}{\overline{Y}^{4}}-2\frac{\overline{X}COV(\frac{X}{n},\frac{Y}{n})}{\overline{Y}^{3}}$

$=\frac{1}{n}(\frac{var(X)}{{\overline{Y}}^{2}}+\frac{\overline{X}^{2}var(Y)}{\overline{Y}^{4}}-2\frac{\overline{X}COV(X,Y)}{\overline{Y}^{3}}) {\color{Green} (2)}$

上述(1)和(2)分别对应图片中的红框和绿框。其中

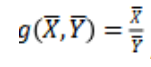
需要注意的是：

所以博客中开头中得到的公式是：

没有了协方差。

Delta Method的结果

博客中对比了传统的和新得到的即

$\frac{var(\bar{y_{t}})+var(\bar{y_{c}})}{y_{c}^{2}}$ 和 $\frac{var(\bar{y_{t}})+(\frac{\bar{y_{t}}}{\bar{y_{c}}})^{2}var(\bar{y_{c}})}{y_{c}^{2}}$ ,前者是下表中的错误方法，后者是Delta Method, Bootstrap是标准

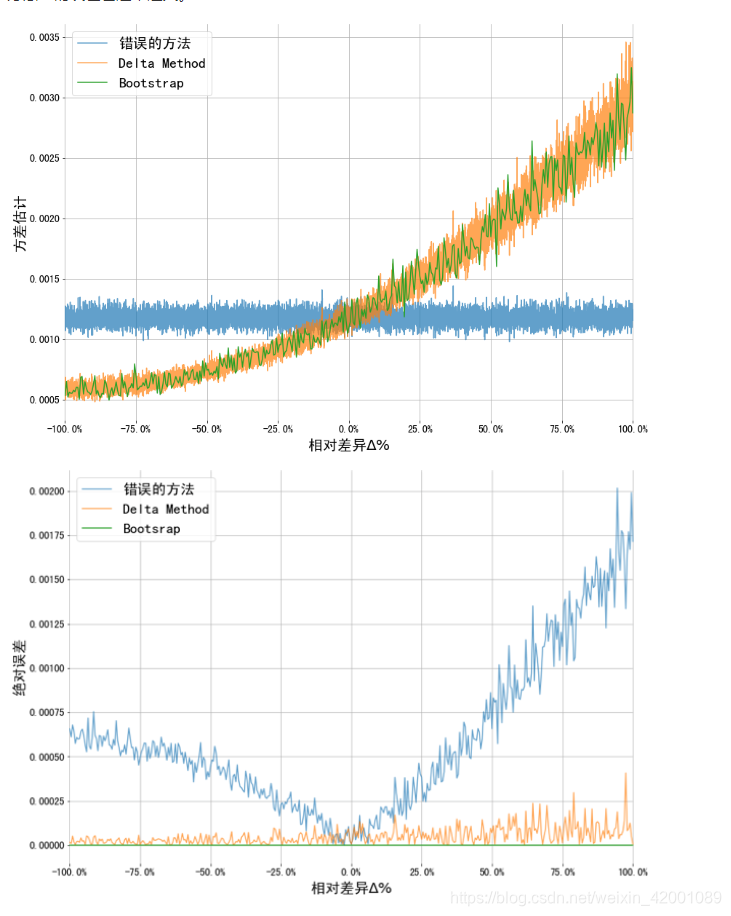
可以看到Delta Method是和Bootstrap标准更趋近。

一些其他有趣的讨论和优化

可以看博客中的特殊情况讨论一节，挺有意思

总结

（1）显著性分析，应用很广泛，一些基本概念要知道，比如原假设H0和备择假设H1，第一类错误和第二类错误，P值

（2）delta method可用于解决非线性多元随机变量方差求解

欢迎关注笔者微信公众号

weixin_42001089

关注

5
点赞
踩
23

收藏

觉得还不错? 一键收藏
1
评论
测试算法有效性：显著性分析

前言今天偶尔刷到一篇博客如下，里面涉及到了很多数学小知识点，基本都是很实用的数学常识，不论从事什么领域，其实都很有帮助，为此记录一下吧。https://mp.weixin.qq.com/s/RLbrf-HNc79P7jaU2Sr29Q下面分多个大标题，记录一下各个使用的点显著性分析这是非常重要了，可以参考https://blog.csdn.net/championkai/article/details/80206704基本上我们要分析两个变量或多个变量之间的差异有多大，就会用到显
复制链接

扫一扫