量子计算 5 量子货币
今天是周日,来个惊喜额外更新一次,今天学习一下不可克隆定理 (No-Cloning Theorem),这个知识点很重要,这是量子信息和量子密码学的基石;以及在其基础上的量子货币,因为不可能克隆,所以可以用来作为货币,这种物理上的不可能,让人感觉相当的高级,毕竟人类估计是无法违背物理学干活。
1 不可克隆定理 (No-Cloning Theorem)
1.1 可以超光速通讯?
在上一集中,我们学习了无通信定理(No-Communication theorem),对一个Bell pair = ∣ 00 ⟩ + ∣ 11 ⟩ 2 =\frac{|00\rangle+|11\rangle}{\sqrt{2}} =2∣00⟩+∣11⟩,张三李四不能超光速交流的原因是因为李四不知道他的量子态是在哪个基下面,但是如果李四可以制造无数个copy,通过不断的测量他是可以知道自己的量子态到底是多少的,这种通过测量一个量子态的多个copy获得其量子态信息的方法叫做量子层析(Quantum State Mography)。
显然这是不行的,原因就是我们不能copy一个量子态:
不可克隆定理 (No-Cloning Theorem):
即不可能构造一个能够完全复制任意量子比特,而不对原始量子比特产生干扰的系统。量子力学的线性特征是这个原理的根本原因。
1.2 证明 1
假设我们要复制一个量子比特
∣
ψ
⟩
=
α
∣
0
⟩
+
β
∣
1
⟩
|\psi\rangle=\alpha |0\rangle+ \beta |1\rangle
∣ψ⟩=α∣0⟩+β∣1⟩,我们也就能用用量子电路来表达这个系统了:

这个
U
U
U实际会做以下操作:
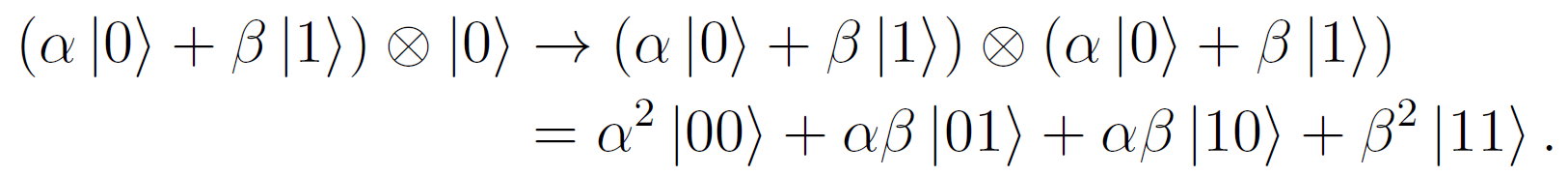
写成矩阵形式:

这个变换
U
U
U不可能是线性的,因为操作的结果含有二次项,因此我们无法通过量子电路去克隆,于是就证明结束了。
1.3 证明 2
首先我们先来说明,酉变换肯定不能改变两个量子态间的内积,因为对于 ∣ v ⟩ , ∣ w ⟩ |v\rangle, |w\rangle ∣v⟩,∣w⟩, 施加酉变换 U U U后是 U ∣ v ⟩ , U ∣ w ⟩ U|v\rangle, U|w\rangle U∣v⟩,U∣w⟩,其内积为 ⟨ v ∣ U † U ∣ w ⟩ = ⟨ v ∣ w ⟩ \langle v|U^{\dagger}U|w\rangle=\langle v | w \rangle ⟨v∣U†U∣w⟩=⟨v∣w⟩。
假设我们用
U
U
U进行克隆,则克隆
∣
v
⟩
,
∣
w
⟩
|v\rangle, |w\rangle
∣v⟩,∣w⟩的操作为:
∣
0
⟩
⊗
∣
v
⟩
→
∣
v
⟩
⊗
∣
v
⟩
∣
0
⟩
⊗
∣
w
⟩
→
∣
w
⟩
⊗
∣
w
⟩
|0\rangle \otimes|v\rangle \rightarrow |v\rangle \otimes|v\rangle \\ |0\rangle \otimes|w\rangle \rightarrow |w\rangle \otimes|w\rangle
∣0⟩⊗∣v⟩→∣v⟩⊗∣v⟩∣0⟩⊗∣w⟩→∣w⟩⊗∣w⟩则两边的内积应该是一样的,左边的内积为:
(
⟨
0
∣
⊗
⟨
v
∣
)
(
∣
0
⟩
⊗
∣
w
⟩
)
=
⟨
0
∣
0
⟩
⟨
v
∣
w
⟩
=
⟨
v
∣
w
⟩
(\langle 0| \otimes \langle v|)(|0\rangle \otimes|w\rangle)=\langle0|0\rangle\langle v|w\rangle=\langle v|w\rangle
(⟨0∣⊗⟨v∣)(∣0⟩⊗∣w⟩)=⟨0∣0⟩⟨v∣w⟩=⟨v∣w⟩
右边的内积为:
(
⟨
v
∣
⊗
⟨
v
∣
)
(
∣
w
⟩
⊗
∣
w
⟩
)
=
⟨
w
∣
v
⟩
⟨
v
∣
w
⟩
=
⟨
v
∣
w
⟩
2
(\langle v| \otimes \langle v|)(|w\rangle \otimes|w\rangle)=\langle w|v\rangle\langle v|w\rangle=\langle v|w\rangle^2
(⟨v∣⊗⟨v∣)(∣w⟩⊗∣w⟩)=⟨w∣v⟩⟨v∣w⟩=⟨v∣w⟩2 两者相等
⟨
v
∣
w
⟩
2
=
⟨
v
∣
w
⟩
\langle v|w\rangle^2=\langle v|w\rangle
⟨v∣w⟩2=⟨v∣w⟩ 因此
⟨
v
∣
w
⟩
\langle v|w\rangle
⟨v∣w⟩为0或者1,所以只有当
∣
v
⟩
|v\rangle
∣v⟩和
∣
w
⟩
|w\rangle
∣w⟩相等或正交的时候,才能进行克隆操作;或者说当
∣
v
⟩
|v\rangle
∣v⟩和
∣
w
⟩
|w\rangle
∣w⟩属于同一个正交基的时候才能进行克隆操作。就像是已经打开了箱子的猫咪,叠加态不重要了,退化成了经典的信息。
2 量子货币 (Quantum money)
对于传统货币,理论上总能做出复制品;对于银行的信用卡,需要相信银行不会把你的存款数目搞错;对于比特币,其一个缺点是耗费资源比较大,整个网络系统扮演的是银行的角色。
如果利用这个不可克隆原理,来搞个量子货币会怎么样呢?来看看对于货币的两个要求:1 货币应该可以被验证真伪; 2 如果已有一些真的货币,应该不能据此造出一张额外的假币;
物理上来说,使用经典信息,同时满足1和2是不可能的,因为经典信息可以被复制。
2.1 Wiesner’s Quantum Money Scheme
某种意义上这是量子信息领域的第一个idea,但是Wiesner提出了这个货币方案之后,就去搬砖了(manual laborer)。
每个货币包括:
- 经典信息 s ∈ { 0 , 1 } n s\in \{0,1\}^n s∈{0,1}n
- n n n个量子比特序列,每个量子比特可能的状态有四个 ∣ 0 ⟩ , ∣ 1 ⟩ , ∣ + ⟩ , ∣ − ⟩ |0\rangle, |1\rangle, |+\rangle, |-\rangle ∣0⟩,∣1⟩,∣+⟩,∣−⟩,有个函数或者数据库 f ( s ) f(s) f(s)可以查到每个量子比特的状态;
2.2 量子货币破解概率
已经获得了证明[1],Wiesner量子货币被破解的最大概率是 ( 3 4 ) n (\frac{3}{4})^n (43)n,当 n n n稍微大一些,这个概率便可以忽略不计。
我们来看一个简单的破解方案来理解一下,假设张三拿了一张量子货币,然后把每一个量子比特都用基 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩来测量,然后把结果制作一张新的货币,那么对于 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩基上的量子比特,这两张货币都能顺利通过检测。对于基为 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩的量子比特,该量子位同时通过检测的概率是 0.5 ∗ 0.5 = 0.25 0.5*0.5=0.25 0.5∗0.5=0.25,这个概率比较小,而且因为你私自测量了本来可以通过验证的货币,导致你可能连真钱也变成假的了。
[1] Molina A, Vidick T, Watrous J. Optimal counterfeiting attacks and generalizations for Wiesner’s quantum money[C]//Conference on Quantum Computation, Communication, and Cryptography. Springer, Berlin, Heidelberg, 2012: 45-64.
2.3 交互式破解方案 1
那假设银行不管你是否验证成功都还给你,你就可以一个一个的去尝试,直到复制好一张,美滋滋;但是银行完全可以在你验证失败后就报警把你抓起来,因为理论上失败的概率超级超级小。
2.4 交互式破解方案 2 (伊利泽-威德曼炸弹, Elitzur-Vaidman Bomb Attack)
但是呢,还有个更聪明的交互式破解方案,这个方案牵扯到前面的 量子计算 3 里面的测量特点,有个“你瞅我干啥(Watched pot effect)”效应,以及今天要看的伊利泽-威德曼炸弹(Elitzur-Vaidman Bomb Attack)。
伊利泽-威德曼炸弹(Elitzur-Vaidman Bomb Attack):
这里的基本思想是,通过一系列测量,在不触发恶性后果的情况下,了解到真实状态的方法。
- 基本规则是,有个量子比特 ∣ b ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |b\rangle=\alpha|0\rangle+\beta |1\rangle ∣b⟩=α∣0⟩+β∣1⟩,我们申请一次,如果没炸弹,就返回 ∣ b ⟩ |b\rangle ∣b⟩;如果有炸弹,就在 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩基下面进行测量,结果为 ∣ 1 ⟩ |1\rangle ∣1⟩的话炸弹会发生爆炸;
- 玩法是,从 ∣ 0 ⟩ |0\rangle ∣0⟩开始,我们施加一个旋转 R ϵ R_\epsilon Rϵ,这个量子比特就变成了 cos ( ϵ ) ∣ 0 ⟩ + sin ( ϵ ) ∣ 1 ⟩ \cos(\epsilon)|0\rangle+\sin(\epsilon)|1\rangle cos(ϵ)∣0⟩+sin(ϵ)∣1⟩,然后进行申请,如果没炸弹就原封不动;如果有炸弹,其爆炸的概率约等于 ϵ 2 \epsilon^2 ϵ2; 这样进行 π 2 ϵ \frac{\pi}{2\epsilon} 2ϵπ次;
- 基本逻辑是,如果有炸弹,其爆炸概率约等于 π ϵ 2 \frac{\pi\epsilon}{2} 2πϵ,相当的小,这个分析过程和 量子计算 3 里面的量子芝诺效应类似,且根据“你瞅我干啥(Watched pot effect)”效应,有很大的概率最后的结果是 ∣ b ⟩ |b\rangle ∣b⟩停留在 ∣ 0 ⟩ |0\rangle ∣0⟩,因为每次你都在 ∣ b ⟩ |b\rangle ∣b⟩很靠近 ∣ 0 ⟩ |0\rangle ∣0⟩的时候测量,每次都坍塌成 ∣ 0 ⟩ |0\rangle ∣0⟩;如果没炸弹,那 ∣ b ⟩ |b\rangle ∣b⟩就转成了 1 1 1;于是,在不引爆炸弹的时候,我们也可以获得是否有炸弹的状态了;
利用这个炸弹去破解Wiesner量子货币:
- 首先也是初始化 ∣ c ⟩ = ∣ 0 ⟩ |c\rangle=|0\rangle ∣c⟩=∣0⟩
- 同样重复
π
2
ϵ
\frac{\pi}{2 \epsilon}
2ϵπ次:
- 施加 R ϵ R_\epsilon Rϵ给 ∣ c ⟩ |c\rangle ∣c⟩
- 施加CNOT给 ∣ c ⟩ ∣ ψ i ⟩ |c\rangle|\psi_i\rangle ∣c⟩∣ψi⟩
- 送去银行验证
- 假设
∣
ψ
i
⟩
=
∣
0
⟩
|\psi_i\rangle=|0\rangle
∣ψi⟩=∣0⟩,每次施加CNOT门都会导致:
CNOT ( cos ( ϵ ) ∣ 0 ⟩ + sin ( ϵ ) ∣ 1 ⟩ ) ∣ 0 ⟩ = cos ( ϵ ) ∣ 00 ⟩ + sin ( ϵ ) ∣ 11 ⟩ \text{CNOT}(\cos(\epsilon)|0\rangle+\sin(\epsilon)|1\rangle)|0\rangle=\cos(\epsilon)|00\rangle+\sin(\epsilon)|11\rangle CNOT(cos(ϵ)∣0⟩+sin(ϵ)∣1⟩)∣0⟩=cos(ϵ)∣00⟩+sin(ϵ)∣11⟩ 在银行测量的时候,只有 ϵ 2 \epsilon^2 ϵ2的不通过概率;同样,整体的不通过概率非常小;这样,在不被抓住的情况下走完这一套, ∣ c ⟩ |c\rangle ∣c⟩都大概率会停留在 ∣ 0 ⟩ |0\rangle ∣0⟩;当 ∣ ψ i ⟩ |\psi_i\rangle ∣ψi⟩为其它 ∣ − ⟩ , ∣ + ⟩ , ∣ − ⟩ |-\rangle, |+\rangle, |-\rangle ∣−⟩,∣+⟩,∣−⟩的时候分析思路类似
于是,就可以在不被抓住的情况下得知每个量子比特的状态!
But,银行完全可以每次测量完之后给你发一张新的量子货币,那就玩不颠了。
2.5 Wiesner量子货币的缺点
最重要的两个缺点是
- 量子状态难以保持,因为你一观察就坍塌了
- 银行需要很大的数据库,但是用一个函数替代的话,需要真随机,也不好搞
再加上,如果只有银行能验证的话,就比较尴尬,我每次用现金都得拿去银行也太麻烦了。
2.6 公钥货币
所以,如果有个公钥,大家都能用公钥进行核对就好了,但是这个在安全性上需要假设张三的算力有限,不然他试算很多次总能破解的。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








