量子计算 20 量子算法 5 Shor Part II: QFT
上回书我们得到了如下所示的量子态,如果要从里面得到想要的周期信息,就要用到今天所介绍的量子傅里叶变换;傅里叶变换在各种学科里的应用超多,本质上可以看成是衡量周期信号的线性变换。
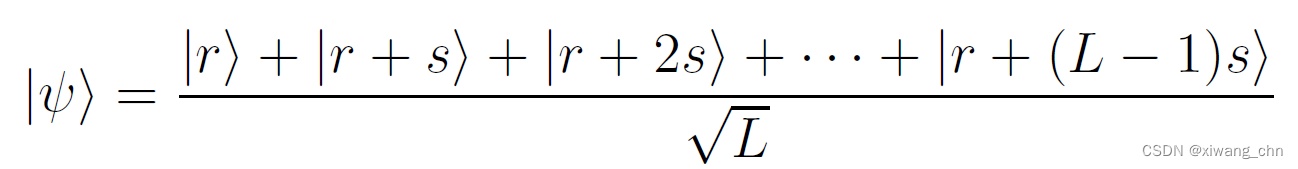
我们要用的量子傅里叶变换QFT就是个矩阵 F Q F_Q FQ: ( F Q ) i , j = ⟨ i ∣ F Q ∣ j ⟩ = w i j Q (F_Q)_{i,j}=\langle i|F_Q|j\rangle=\frac{w^{ij}}{\sqrt{Q}} (FQ)i,j=⟨i∣FQ∣j⟩=Qwij 其中 w i j = e 2 π i / Q w^{ij}=e^{2\pi i/Q} wij=e2πi/Q是1在复数范围的Q次根;通过验算向量的单位正交性,可知 F Q F_Q FQ是酉矩阵;其中 F 2 = H F_2=H F2=H,即二阶的 F Q F_Q FQ代表的就是Hadamard门。
接下来的两个问题:1 如何用QFT来获取有效周期信息?2 如何获取较小的量子电路来执行QFT?
对于第一个问题,其实直觉上可以感觉到,当我们采样或者测量的某个周期和真实周期相符时,获得的结果的量子幅会相同而一致叠加实现constructive interference,如果不一致时,获得的结果也会呈现周期变换最后叠加结果为零即destructive interference。
对第二个问题,我们将从快速傅里叶变换FFT中得到启发,最终以 O ( log 2 Q ) O(\log^2 Q) O(log2Q)或 O ( log Q log log Q ) O(\log Q \log\log Q) O(logQloglogQ)个门来建立量子电路。
1 Fast Fourier Transform (FFT)
给定向量 v ∈ C Q v\in \mathbb{C}^Q v∈CQ,使用FFT计算 v v v的傅里叶变换 F Q v F_Q v FQv,简单的经典计算方法复杂度为 O ( Q 2 ) O(Q^2) O(Q2),使用FFT则仅需要 O ( Q log Q ) O(Q\log Q) O(QlogQ)数值操作。
我们先来看
F
2
F_2
F2,第一行像是不断乘以
w
0
w^0
w0,第二行不断乘以
w
1
w^1
w1
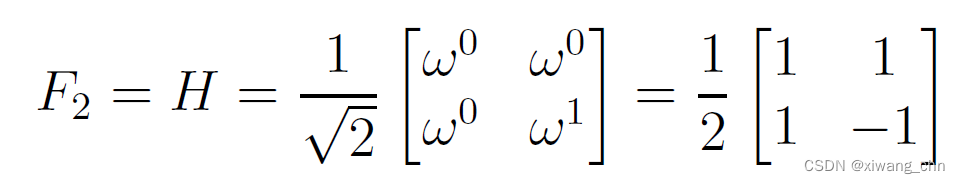
再来看
F
4
F_4
F4,第一行像是不断乘以
w
0
w^0
w0,第二行不断乘以
w
1
w^1
w1,第三行像是不断乘以
w
2
w^2
w2,第四行不断乘以
w
3
w^3
w3:

且,我们将列的序号,以二进制编码,比如0=00,1=01,2=10,3=11,然后将二进制编码的最小位提高最高位上,则0=00->00=0,1=01->10=2,2=10->01=1,3=11->11=3,效果相当于将原来的偶数列都放到左边,原来的奇数列都放到右边。
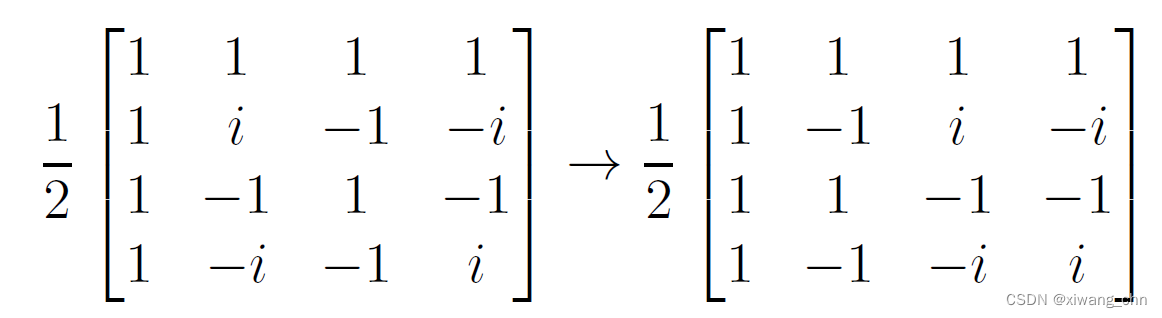
得到:
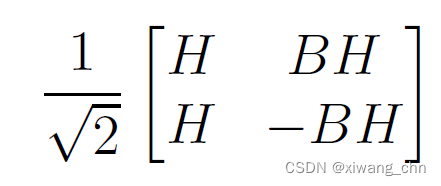
其中
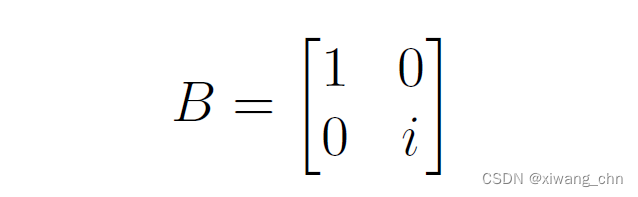
对于
F
8
F_8
F8做同样的操作可得:

递推公式:
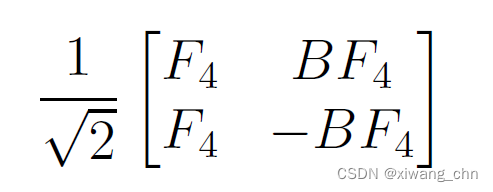
其中:
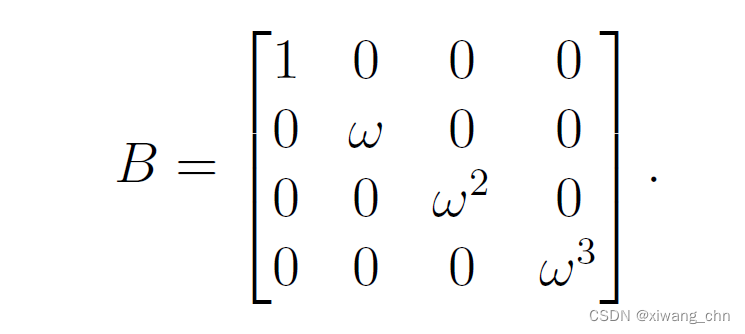
一般的递推公式可得:
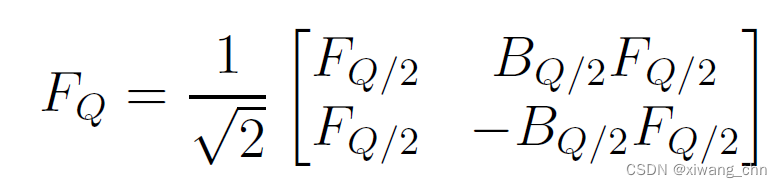
其中
B
Q
/
2
B_{Q/2}
BQ/2:

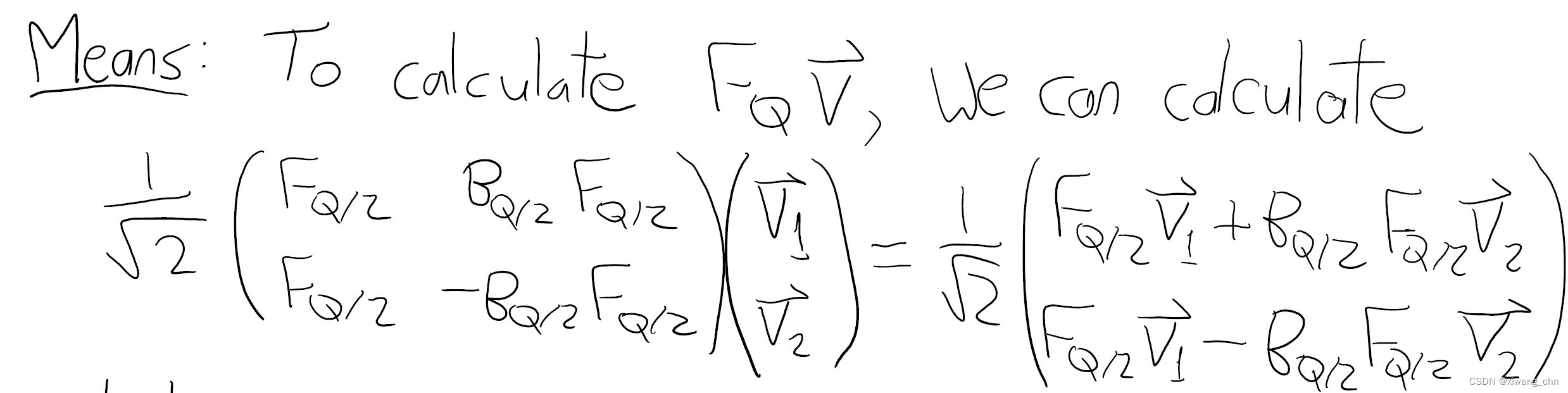
因此复杂度为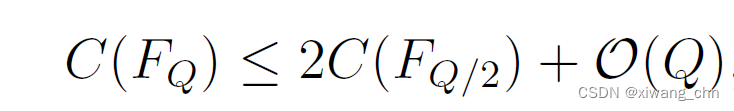
从该递推公式可得
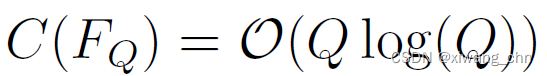
2 Quantum Fourier Transform and Circuit
在量子计算中,我们希望构建一个量子电路,能自动的实现以上所述的量子傅里叶变换 ∣ ψ ⟩ → F Q ∣ ψ ⟩ |\psi\rangle\rightarrow F_Q|\psi\rangle ∣ψ⟩→FQ∣ψ⟩,其中 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩是具有 log 2 Q \log_2 Q log2Q个qubit的量子态。
现在我们通过小的量子门计算来构建量子傅里叶变换的递推过程。
- 首先,先拓展既有的
F
Q
/
2
F_{Q/2}
FQ/2,每增加一个qubit,矩阵的维度其实是要乘以2的,因为多了一个维度,且维度的可能取值有两个,因此先对
F
Q
/
2
F_{Q/2}
FQ/2通过张量积对第一个多的比特进行单位矩阵操作,即
I
2
⊗
F
Q
/
2
I_2\otimes F_{Q/2}
I2⊗FQ/2,得到:
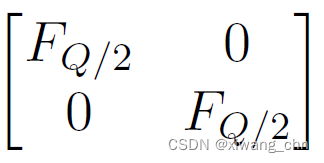
- 然后我们的
B
Q
/
2
B_{Q/2}
BQ/2,其实相当于是对除了所增加的第一个qubit之外的其它比特进行操作,在这里引进controlled-B,即当第一个bit为1的时候进行
B
Q
/
2
B_{Q/2}
BQ/2操作:
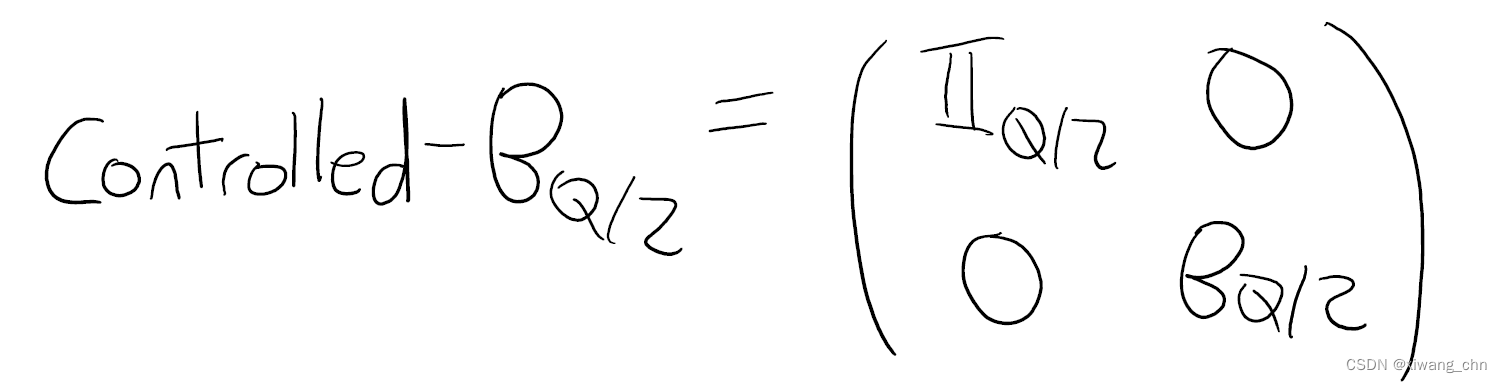
- 第三步是对新增的第一个qubit进行
H
H
H门操作,其相当于,
H
⊗
I
Q
/
2
H\otimes I_{Q/2}
H⊗IQ/2,得到了:
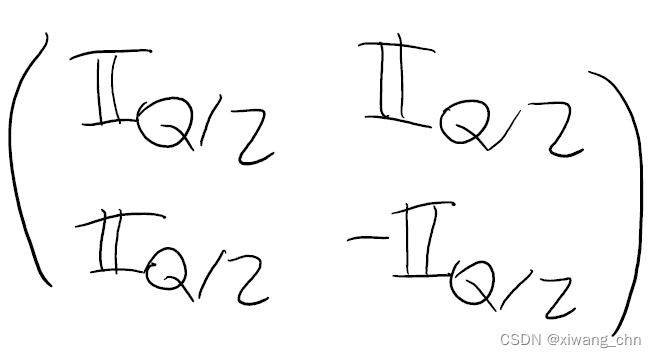
- 这一步其实是将我们一致视为添加的第一个qubit,也是最高位(most significant)的qubit给调回到最低位(least significant)上来。
最后得到的递推形式的量子电路如图:
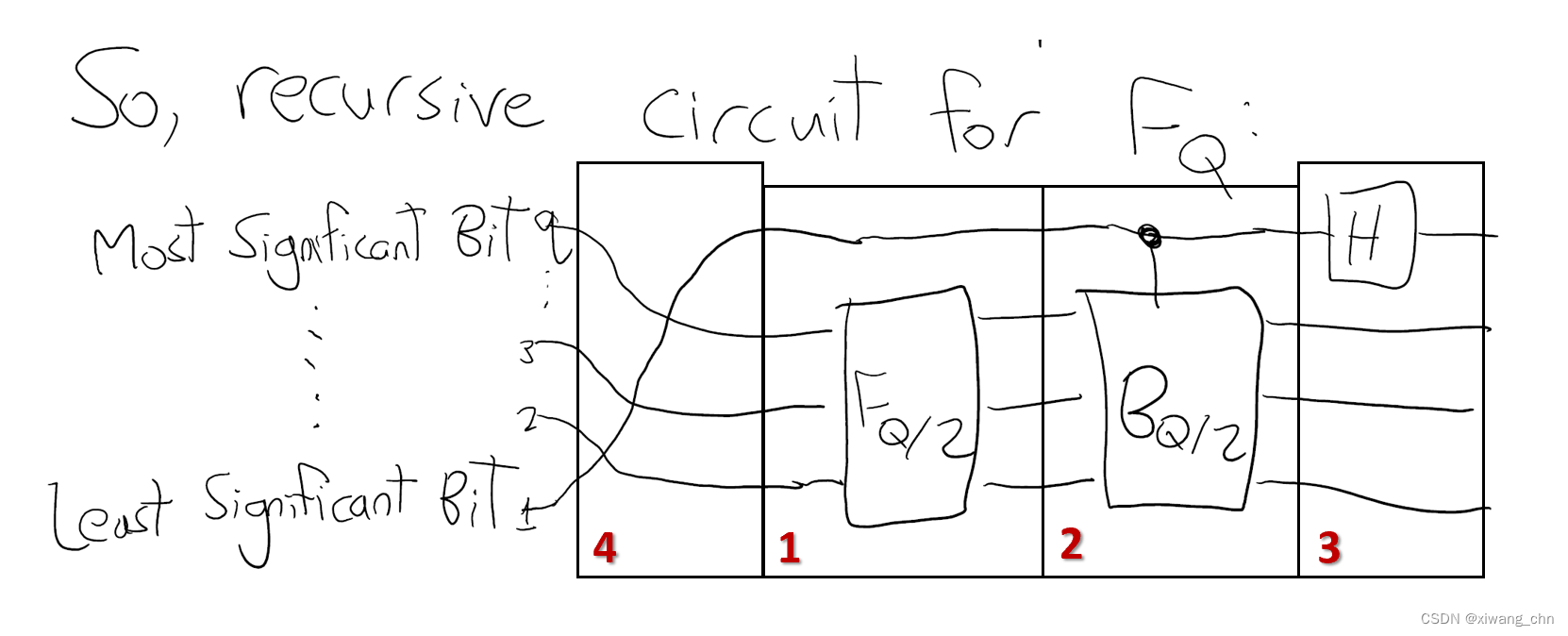
图中的1即代表了上述第一步操作,相当于对增加的新qubit做单位变换或者不做操作;
图中的2代表了上述的第二部操作,即施加controlle-B,操作,现在的累积操作如下:
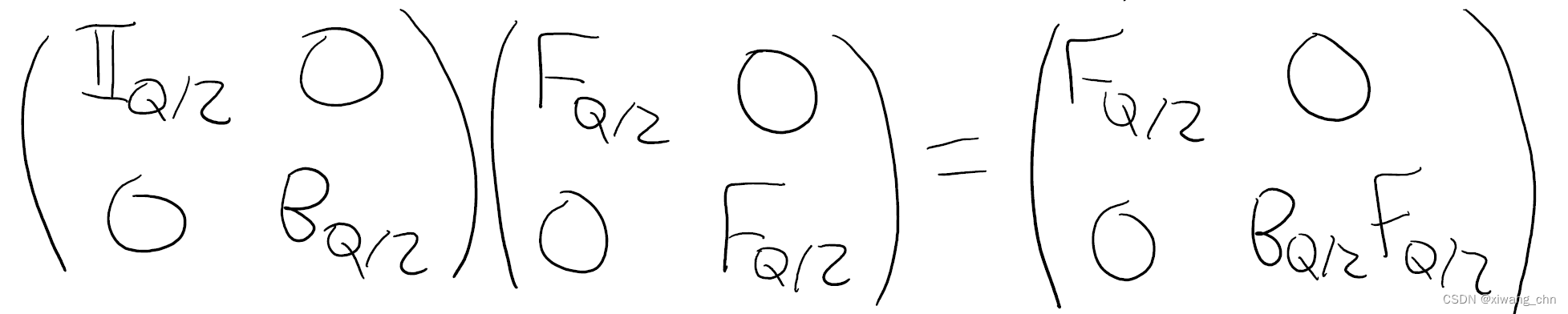
图中的3代表了上述第三步操作,即对新增的第一个qubit进行H门,累积操作如下:
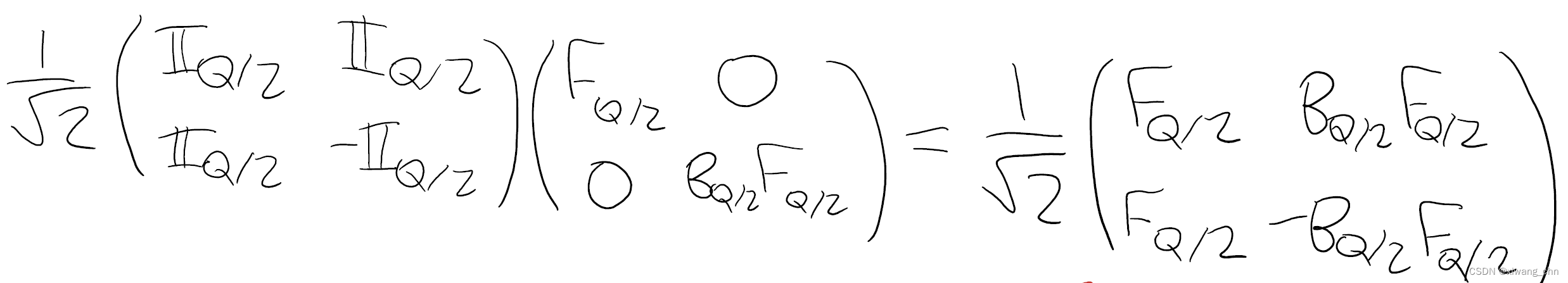
可以发现经过这三步操作我们其实已经实现了从
F
Q
/
2
F_{Q/2}
FQ/2到
F
Q
F_{Q}
FQ的递推,操作4,其实是效仿FFT中对列的调整,即将least significant的qubit放到了most significant上,这我们在一开始,即图中的1中,就已经完成了,因此我们就得到了
F
Q
F_{Q}
FQ。
还有的问题是
B
Q
/
2
B_{Q/2}
BQ/2是怎么执行的,如图:
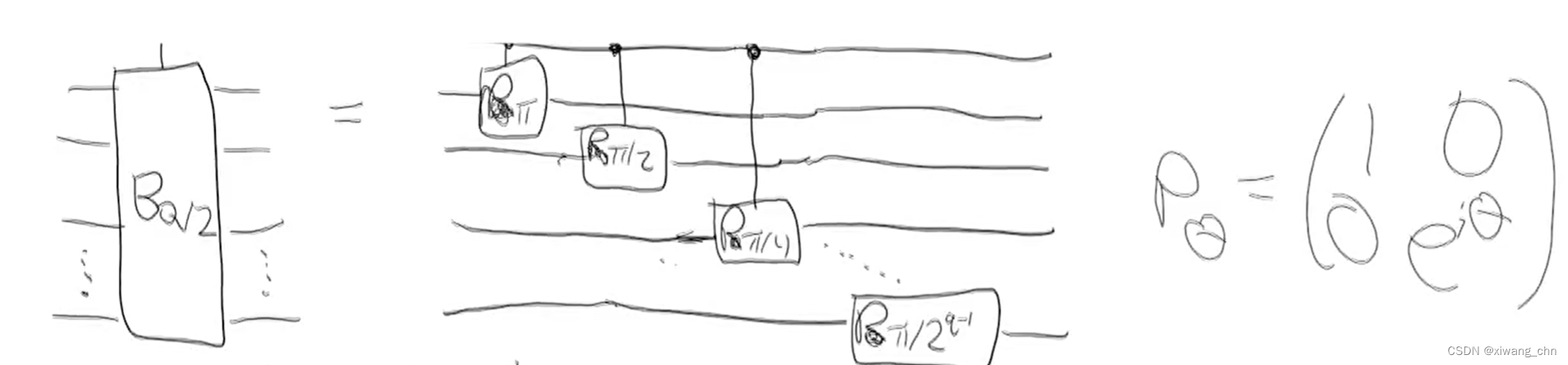
因此从
F
Q
/
2
F_{Q/2}
FQ/2到
F
Q
F_{Q}
FQ额外需要
log
2
Q
\log_2 Q
log2Q个门,则得复杂度:
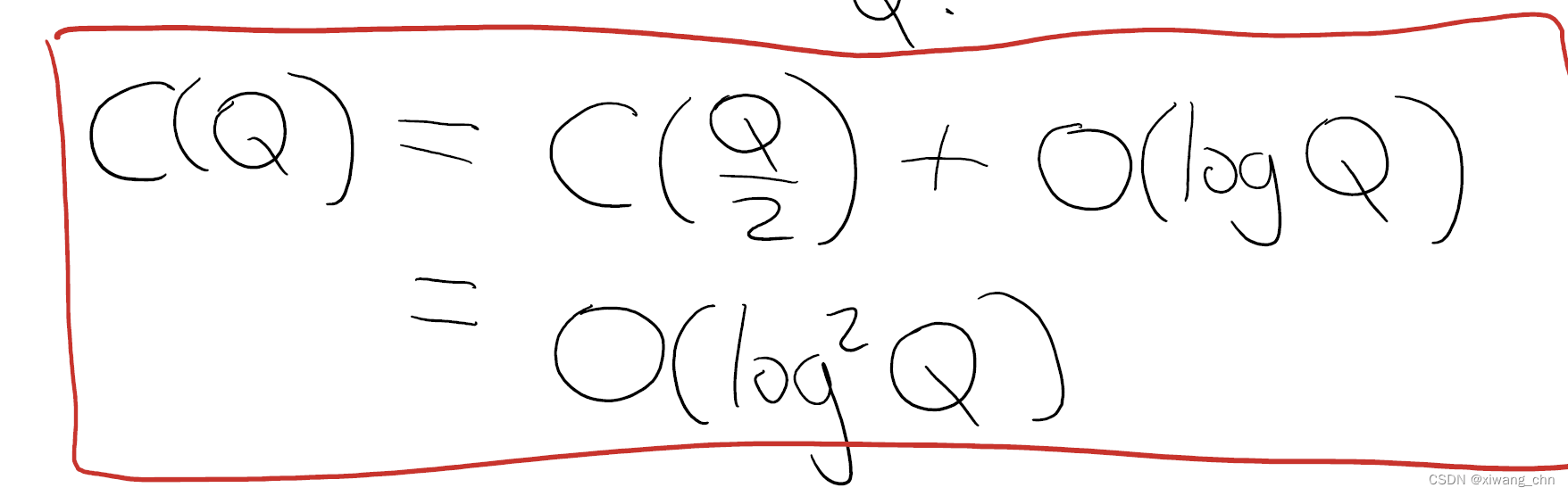
当我们忽略B中足够小的phase shift的时候,可得到
O
(
log
Q
log
log
Q
)
O(\log Q \log\log Q)
O(logQloglogQ)复杂度的量子电路。而phase shift貌似也是我们除了H门之外用到的第二个量子门了。






















 387
387











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








