量子计算 13 经典通用门 Classical Universal gates
上回书说到,想要搭建量子计算机,也就是要涉及量子电路,那应该采取什么样的量子门呢?哪些门能完成所有的计算呢?
本回书,先来讨论经典的通用门,有些门(reversible)也可以用在量子电路里面,这就是下回书的主题啦。
首先介绍经典通用门,是怎么实现任意的布尔函数(Boolean function): f : { 0 , 1 } n → { 0 , 1 } f:\{0,1\}^n\rightarrow \{0,1\} f:{0,1}n→{0,1}; 然后介绍可逆通用门;因为这些通用门实现任意逻辑函数需要ancilla bits,最后介绍可以将使用的ancilla bits复位的Uncomputing。
1 经典通用门 (Universal gates)
Theorem: { AND , OR , NOT } \{\text{AND}, \text{OR}, \text{NOT}\} {AND,OR,NOT} is universal.
Proof: Given any
f
:
{
0
,
1
}
n
→
{
0
,
1
}
f: \{0,1\}^n\rightarrow\{0,1\}
f:{0,1}n→{0,1}, look at its truth table.

大概的意思就是,任意给一个如图所示的函数,把结果为1的输入
x
,
y
,
z
x,y,z
x,y,z,用用NOT表示0,用AND表示一组
x
,
y
,
z
x,y,z
x,y,z,用OR表示几组
x
,
y
,
z
x,y,z
x,y,z一起,就可以实现该函数,所以
{
AND
,
OR
,
NOT
}
\{\text{AND}, \text{OR}, \text{NOT}\}
{AND,OR,NOT} 是通用的。
另外, { AND , NOT } \{\text{AND}, \text{NOT}\} {AND,NOT} 也是通用的,因为OR可以由他俩构成,也如上图所示;单个的与非门 { NAND } \{ \text{NAND}\} {NAND}和或非门 { NOR } \{ \text{NOR}\} {NOR}也是通用的;
而 { AND , OR } \{\text{AND}, \text{OR}\} {AND,OR}不是通用的,因为这两个门组成的函数一定是Monotone (单调)的,因为当我将输入从0变成1的时候,结果一定不会从1变成0。
另外 { NOT , XOR } \{\text{NOT}, \text{XOR}\} {NOT,XOR},即非门和异或门,也不通用的,因为异或相当于(x+y)mod2,而非相当于(x+y)mod2,而与相当于xy,所以可以看到这俩门只能进行线性运算,缺了xy不能进行非线性计算。
2 可逆通用门
由计算热力学(thermodynamics of computation)兴起的,想探索计算耗费能量,最后知道,擦除bit才会额外耗费热量,而擦除的bit也不是凭空消失了,根据物理上可逆的原则,其实可以知道bit只是转化成了热量的形式耗散掉了,但是这似乎和可逆通用门关系不大。
什么是可逆门?
一个k-bit的可逆门就是k-bit string的一个排列间的映射(permutation),一对一的将前后的状态对应起来,也能对应回去,所以可逆;比如一个CNOT门,
CNOT
∣
x
,
y
⟩
=
∣
x
,
x
⊕
y
⟩
\text{CNOT}|x,y\rangle=|x,x\oplus y\rangle
CNOT∣x,y⟩=∣x,x⊕y⟩,其就相当于一个permutation矩阵,这里的permutation相当于是原始状态与其重新排列后的状态一一对应,并不仅仅是01本身的0和1的位置转变:

没有2-bit的通用可逆门
列举检查一下即可;2-bit可逆门都是NOT,CNOT,SWAP的组合;甚至不能实现一个AND门;
Toffoli/CCNOT门 (3-bit 通用可逆门)

Toffoli或者CCNOT,跟CNOT相似,即前两个bit为真,则翻转第三个bit: ∣ x , y , z ⟩ → ∣ x , y , z ⊕ x y ⟩ |x,y,z\rangle\rightarrow |x,y,z\oplus xy\rangle ∣x,y,z⟩→∣x,y,z⊕xy⟩;
通过设置前两个bit为1,可以实现NOT门:
∣
1
,
1
,
z
⟩
→
∣
1
,
1
,
z
⊕
1
⟩
|1,1,z\rangle\rightarrow |1,1,z\oplus 1\rangle
∣1,1,z⟩→∣1,1,z⊕1⟩;通过设置第三个bit为0,可以实现AND门:
∣
x
,
y
,
0
⟩
→
∣
x
,
y
,
0
⊕
x
y
⟩
|x,y,0\rangle\rightarrow |x,y,0\oplus xy\rangle
∣x,y,0⟩→∣x,y,0⊕xy⟩;这里面异或门
⊕
\oplus
⊕的性质见附录;所以Toffoli门或CCNOT门是通用门。

如图,通过Toffoli门可以实现MAJ(x,y,z)函数,即取主要的输出,MAJ(0,0,1)=0。但是MAJ是不可逆的操作,为什么是由可逆的Toffoli门组成的呢?因为多了一些辅助的ancilla bits或称garbage bits,这些辅助的bits使得这个电路是可逆的。
Fredkin/CSWAP门 (3-bit 通用可逆门)
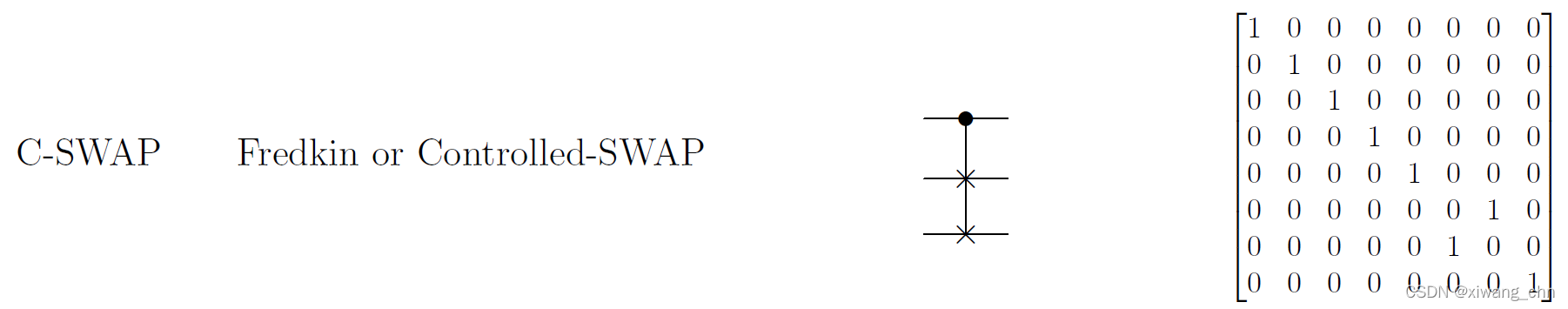

如图,可以实现
x
AND
y
x \text{AND}y
xANDy的操作

如图,可以实现
NOT
x
\text{NOT}x
NOTx的操作
所以,Fredkin/CSWAP门是通用可逆门。
但是Fredkin/CSWAP门有个限制,就是不能改变1的数量,因为只能作一个交换,也就是保持hamming weight不变,所以Fredkin/CWAP能实现所有Boolean function,但不能实现所有Reversible transformation
3 Uncomputing
Toffoli门(Fredkin不是),可以在更广义的情况下作为通用门,即对 { 0 , 1 } n \{0,1\}^n {0,1}n的任意permutation σ \sigma σ,或任意reversible transformation,都可以仅用Toffoli门实现 ∣ x ⟩ → ∣ σ ( x ) ⟩ |x\rangle\rightarrow|\sigma(x)\rangle ∣x⟩→∣σ(x)⟩ 如果要用到一些Ancilla或Garbage bits的话,要在计算结束的时候把他们复原。
Proof part I
给定任意布尔电路
C
\mathcal{C}
C(不一定可逆),可以用Toffoli电路实现以下可逆转换:
∣
x
,
a
⟩
→
∣
x
,
a
⊕
C
(
x
)
⟩
|x,a\rangle\rightarrow |x,a\oplus \mathcal{C}(x)\rangle
∣x,a⟩→∣x,a⊕C(x)⟩,采用如下图所示的uncomputing的技术

在这里电路
C
\mathcal{C}
C和
C
−
1
\mathcal{C}^{-1}
C−1显然可以由可逆通用的Toffoli电路实现,计算的结果在中间用CNOT存储起来,最下面的bit可以更泛化为
∣
a
⟩
|a\rangle
∣a⟩,则此uncomputing电路:
∣
x
,
a
⟩
→
∣
x
,
a
⊕
C
(
x
)
⟩
|x,a\rangle\rightarrow |x,a\oplus \mathcal{C}(x)\rangle
∣x,a⟩→∣x,a⊕C(x)⟩当然
a
=
0
a=0
a=0的时候
0
⊕
C
(
x
)
=
C
(
x
)
0\oplus \mathcal{C}(x)=\mathcal{C}(x)
0⊕C(x)=C(x),也就是
∣
x
,
0
⟩
→
∣
x
,
C
(
x
)
⟩
|x,0\rangle\rightarrow |x, \mathcal{C}(x)\rangle
∣x,0⟩→∣x,C(x)⟩
这里的前提是 C ( x ) \mathcal{C(x)} C(x)不是量子的,因为qubit根据不可克隆定理是复制不了的。
Proof part II
现在要做 ∣ x ⟩ → ∣ σ ( x ) ⟩ |x\rangle\rightarrow|\sigma(x)\rangle ∣x⟩→∣σ(x)⟩
也就是从 ∣ x , 0 n ⟩ → ∣ σ ( x ) , 0 n ⟩ |x,0^n\rangle\rightarrow|\sigma(x),0^n\rangle ∣x,0n⟩→∣σ(x),0n⟩
通过Proof I中的uncomputing可以得到: ∣ x , 0 n ⟩ → ∣ x , σ ( x ) ⟩ |x,0^n\rangle\rightarrow|x, \sigma(x)\rangle ∣x,0n⟩→∣x,σ(x)⟩,SWAP一下就得到了 ∣ σ ( x ) , x ⟩ | \sigma(x),x\rangle ∣σ(x),x⟩,然后再用uncomputing算一下 σ − 1 \sigma^{-1} σ−1就得到了 ∣ σ ( x ) , x ⊕ σ − 1 ( σ ( x ) ) ⟩ | \sigma(x),x\oplus\sigma^{-1}(\sigma(x))\rangle ∣σ(x),x⊕σ−1(σ(x))⟩,也就是 ∣ σ ( x ) , x ⊕ x ⟩ = ∣ σ ( x ) , 0 n ⟩ | \sigma(x),x\oplus x\rangle=| \sigma(x),0^n\rangle ∣σ(x),x⊕x⟩=∣σ(x),0n⟩,证明完毕。
4 可逆运算与加密运算的矛盾?
从Proof I里面的uncomputing,我们看到运算 ∣ x ⟩ → ∣ σ ( x ) ⟩ |x\rangle\rightarrow|\sigma(x)\rangle ∣x⟩→∣σ(x)⟩貌似很容易就能逆过来,如果这样那就没法加密了,因为加密的前提就是逆运算不好算。不过注意的是上面的具体计算是 ∣ x , a ⟩ → ∣ x , a ⊕ σ ( x ) ⟩ |x,a\rangle\rightarrow|x,a\oplus\sigma(x)\rangle ∣x,a⟩→∣x,a⊕σ(x)⟩,即要知道 x x x才能进行运算,那都要知道 x x x了也就没有逆运算的必要了。
附录:常见门操作
-
与AND: A B AB AB
-
或OR: A + B A+B A+B
-
非NOT: A ˉ \bar{A} Aˉ
-
异或XOR:相同为0,不同为1;与0异或不变,与1异或翻转; ( A + B ) mod 2 (A+B)\text{mod}2 (A+B)mod2; A ⊕ B = A B ˉ + A ˉ B A\oplus B=A\bar{B}+\bar{A}B A⊕B=ABˉ+AˉB;满足异或结合律;
-
与非:AND NOT
-
或非:OR NOT
-
CNOT: CNOT ∣ x , y ⟩ = ∣ x , x ⊕ y ⟩ \text{CNOT}|x,y\rangle=|x,x\oplus y\rangle CNOT∣x,y⟩=∣x,x⊕y⟩

-
Toffoli, CCNOT: ∣ x , y , z ⟩ → ∣ x , y , x ⊕ x y ⟩ |x,y,z\rangle\rightarrow |x,y,x\oplus xy\rangle ∣x,y,z⟩→∣x,y,x⊕xy⟩

-
Fredkin or CSWAP
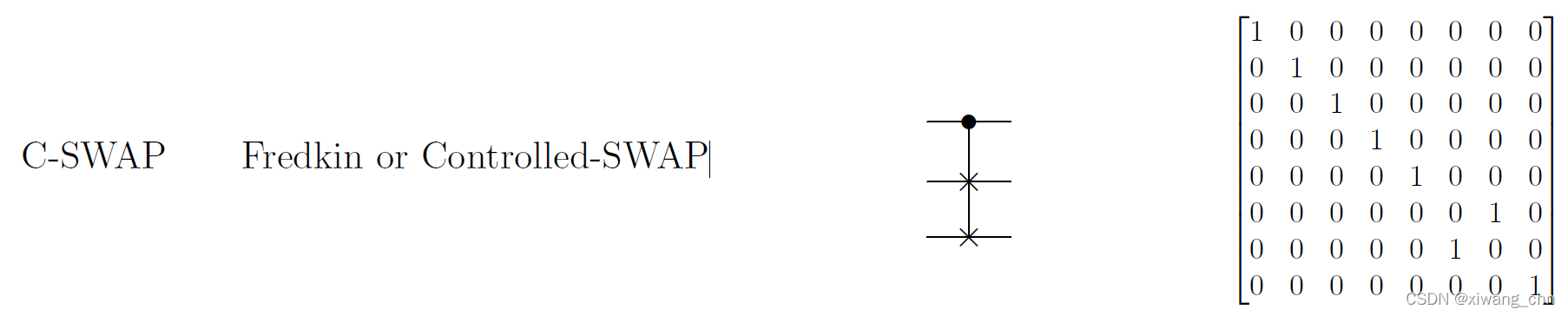








 本文介绍了量子计算中的经典通用门,如AND, OR, NOT及其组合,证明了它们的通用性。接着探讨了可逆门的概念,包括3-bit的通用可逆门Toffoli/CCNOT和Fredkin/CSWAP门。同时,解释了Uncomputing过程以及可逆运算与加密运算之间的关系。文章还提到了可逆运算在保持能量效率方面的意义,并讨论了其与经典加密的冲突点。
本文介绍了量子计算中的经典通用门,如AND, OR, NOT及其组合,证明了它们的通用性。接着探讨了可逆门的概念,包括3-bit的通用可逆门Toffoli/CCNOT和Fredkin/CSWAP门。同时,解释了Uncomputing过程以及可逆运算与加密运算之间的关系。文章还提到了可逆运算在保持能量效率方面的意义,并讨论了其与经典加密的冲突点。
















 1007
1007

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








