从信息论到机器学习的损失函数

从信息论到机器学习的损失函数

信息论

最大互信息原则：多层神经网络的突触连接以这样一种方式进行；在网络的每个处理阶段 ，当进行信号变换时，为保留的信息量达到最大，要遵从一定的约束条件。

感知系统的信息论作用：感知机制的一个主要功能是减小刺激的冗余，以一种比它冲击接收器的形式更经济的公式对信息进行描述或编码。

一个随机变量x的每一个出现可看作一个消息。严格说，如果随机变量x的幅度值是连续的，则它带着无穷的信息，但这是没有意义的，这就是可以把x的值一致量化到有限的离散水平。把x看成是离散的随机变量，其模型为
x = { x k ∣ k = 0 , ± 1 , ⋯   , ± k } x=\left\{x_{k} | k=0, \pm 1, \cdots, \pm k\right\} x={xk​∣k=0,±1,⋯,±k}

让事件$x=x_k$以 $p_k=p\left(x=x_k\right)$ 的概率发生，其中这个概率在0-1之间，且
$$\sum _{k=-k}^k{p}_k=1$$
首先，我们定义观察到具有概率p_k 的事件$x=x_k$后获得的信息增益量为对数函数
$$I\left(x_k\right)=\log \left(\frac{1}{p_k}\right)=-\log p_k$$

(即信息量与事件发生概率成反比)底数为𝑒时，单位是奈特,底数为2时；单位是比特或香农。由此得到，$I\left(x_k\right)=0$ ，当$p_k=1$ 。信息量$I\left(x_k\right)$也是一个具有概率$p_k$的离散随机变量。$I\left(x_k\right)$全部2𝑘+1个离散数值上的平均值上的平均值定义为：
$$H(X)=E\left(I\left(x_k\right)\right)=\sum _{k=-k}^k{p}_{k}I\left(x_k\right)=-\sum _{k=-k}^k{p}_k\log p_k$$

𝐻(𝑋)即为一个可取离散随机变量𝑥的熵，意义为每一个消息所携带的消息的平均量。

==
注：以下用I(a)表示a事件发生的信息量有两个事件a,b：
1、0<p(a)<p(b)<1,则 I(a)>I(b)
2、p(a)=0,则 I(a)->infinity
3、p(a)=1,则 I(a)=0
4、p(a,b)=p(a)p(b),I(a,b)=I(a)+I(b)
经过严格证明满足上述条件的信息函数一定有些形式（充分必要）：I(a)=-logp(a) 这里的底数是大于1的均可。

==

接下来引入微分熵的概念，h(x)为连续随机变量的熵定义为x的微分熵
$$h(x)=-{\int }_{-\infty }^{\infty }{p}_x(x)\log p_x(x)dx=-E\left[\log p_x(x)\right]$$
其与H(x)联系为$$H(x)=h(x)-\underset{\delta \to 0}{\lim }\log p_x(x)$$上式中x为单值变量。

最大熵原则：当根据不完整的信息作为依据进行推断时，应该由满足分布限制条件的具有最大熵的概率分布推得。熵的概念在概率分布空间定义一种度量，使得具有较高熵的分布比其他的分布具有更大的值。

互信息

考虑一对连续随机变量𝑋和𝑌，这两者是相关的。由
$$p(x,y)=p(x)p(y|x)$$以及微分熵的定义$$h(X,Y)=h(X)+h(Y|X)=h(Y)+h(X|Y)$$
h(X,Y)为X和Y的联合微分熵，h(Y|X)为条件微分熵。

令
$$\begin{array}{rl}I(X;Y)=& h(X)-h(X|Y)=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{P}_{X,Y}(x,y)\log P_X(x)dxdy\\ & +{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{P}_{X,Y}(x,y)\log P_X(x/y)dxdy\\ =& {\int }_{-\infty }^{\infty }{P}_{X,Y}(x,y)\log \left(\frac{P_{X,Y}(x,y)}{P_X(x)P_Y(y)}\right)dxdy\end{array}$$
这一熵差称为系统输入𝑥和系统输出𝑌之间的互信息,意义为观察系统输出𝑌所决定的系统输入𝑥的不确定性。

相对熵

对于同一个随机变量𝑥有两个单独的概率分布𝑃(𝑋)和𝑄(𝑋)。即针对同一事件，有两个概率分布𝑃（代表真实概率）和𝑄（代表模型概率）可以用相对熵来衡量这两个分布差异：
$$D_{p\Vert q}={\int }_{-\infty }^{\infty }{P}_X(x)\log \left(\frac{P_X(x)}{Q_X(x)}\right)dx=E_{x\sim p}\left[\log \left(\frac{P_X(x)}{Q_X(x)}\right)\right]=E_{x\sim P}[\log P(x)-\log Q(x)]$$
相对熵又被称为KL散度。

==
注：
$$由I(X;Y)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{P}_{X,Y}(x,y)\log \left(\frac{P_{X,Y}(x,y)}{P_X(x)P_Y(y)}\right)dxdy$$

$$=D_{P_{X,Y}\Vert P_X(x)P_Y(y)}$$

即𝑋和𝑌之间的互信息𝐼(𝑋;𝑌)等于联合概率密度函数$P_{X,Y}(x,y)$以及概率密度函数𝑃_𝑋 (𝑥)和𝑃_𝑌 (𝑦)的积的相对熵。

==

交叉熵

$$H(P,Q)=H(P)+D_{KL}(P\Vert Q)$$

$$=-E_{x\sim p}[\log P(x)]+E_{x\sim p}\left[\log \frac{P(x)}{Q(x)}\right]$$

$$=-E_{x\sim p}[\log Q(x)]=-{\int }_{-\infty }^{\infty }P(x)\log Q(x)dx$$

或是$$=-\sum _{x}P(x)\log Q(x)$$

==
注：并且由此式可以看出只有当𝑃(𝑥)与𝑄(𝑥)完全一致时 𝐻(𝑃,𝑄)=𝐻(𝑃)，其他情况都是𝐻(𝑃,𝑄)>𝐻(𝑃)；
综上相对熵与交叉熵，我们衡量两个分布的差异本来是用相对熵（𝐾𝐿散度），但是当𝑃(𝑥)固定时，即事件𝑥满足的先验分布一定时，由𝐻(𝑃,𝑄)=𝐻(𝑃)+𝐷_𝐾𝐿 (𝑃||𝑄)也即𝐻(𝑃)不变，那么我们可以用𝐻(𝑃,𝑄)即𝑃和𝑄的交叉熵来代替相对熵来评估模型！！！

==

logistic回归

在𝑙𝑜𝑔𝑖𝑠𝑡𝑖𝑐回归中𝑠𝑖𝑔𝑚𝑜𝑖𝑑函数的输出了表征了当前样本标签为1的概率：
$$h_{\theta }(x)=P(y=1|x)$$

因此，样本标签为0的概率就可以表达成:
$$1-h_{\theta }(x)=P(y=0|x)$$

代入交叉熵损失函数中，即为:
$$y\log h_{\theta }(x)+(1-y)\log \left(1-h_{\theta }(x)\right)$$

由于上式是在最后一层所分出的一个类的一个样本的𝑙𝑜𝑠𝑠 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
那么整个样本的cost 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛为:

$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}\log h_{\theta }{\left(x^{(i)}\right)}_k+\left(1-y_k^{(i)}\right)\log \left(1-h_{\theta }{\left(x^{(i)}\right)}_k\right)\right]$$

(由于平方误差函数用于线性回归中很好，但是当用于逻辑回归时呈现的是非凸状态，有很多鞍点，不容易取到最值，所以在逻辑回归中，最常用的是交叉熵代价函数，在神经网络中也会用到。)

从最大似然角度看，设
$$P\left({\hat{y}}^{(i)}=1|x^{(i)};\theta \right)=h_{\theta }\left(x^{(i)}\right)$$

则$$P\left({\hat{y}}^{(i)}=0|x^{(i)};\theta \right)=1-h_{\theta }\left(x^{(i)}\right)$$

将上述两种情况整合到一起：
$$P(y|x)={\hat{y}}^y(1-\hat{y}{)}^{1-y}$$

那么对于多个样本的概率函数推导为：
$$p(y|x)=\left[p\left({\hat{y}}^{(i)}=1|x^{(i)};\Theta \right)\right]y^{(i)}\left[p\left({\hat{y}}^{(i)}=0|x^{(i)};\Theta \right)\right]\left(1-y^{(i)}\right)$$

将概率取对数，其单调性不变：
$$\log P\left({\hat{y}}^{(i)}=1|x^{(i)};\theta \right)=\log h_{\theta }\left(x^{(i)}\right)$$

$$\log P\left({\hat{y}}^{(i)}=0|x^{(i)};\theta \right)=\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)$$

$$\log p(y|x)=\log \left\{\left[p\left({\hat{y}}^{(i)}=1|x^{(i)};\Theta \right)\right]y^{(i)\ast }\left[p\left({\hat{y}}^{(i)}=0|x^{(i)};\Theta \right)\right]\left(1-y^{(i)}\right)\right\}$$

$$\begin{array}{l}=y^{(i)}\log P\left({\hat{y}}^{(i)}=1|x^{(i)};\theta \right)+\left(1-y^{(i)}\right)\log P\left({\hat{y}}^{(i)}=0|x^{(i)};\theta \right)\\ =y^{(i)}\log h_{\theta }\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)\end{array}$$

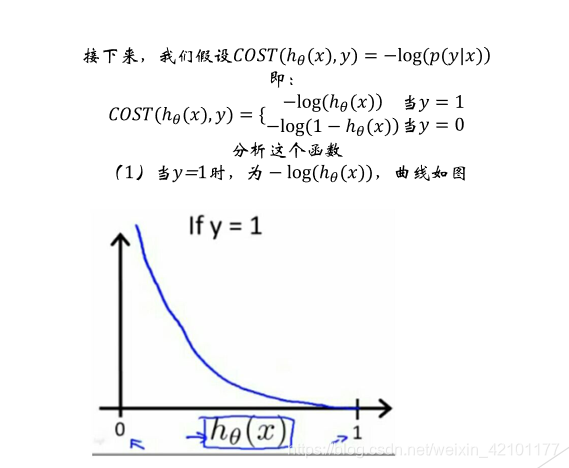
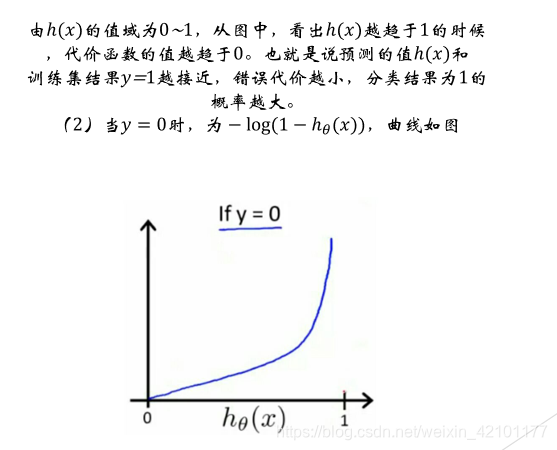
当ℎ(𝑥)的值趋于0时，代价函数的值越趋于0，也就是预测的值和训练集真实值越接近，错误代价越小，此时，分类为0的概率1−ℎ(𝑥)接近于1。综上所述，所设函数符合代价函数要求，即所设函数可以作为代价函数

由以上表征正确的概率含义可知，我们希望其值越大，模型对数据的表达能力@越好。而我们在参数更新或衡量模型优劣时是需要一个能充分反映模型表现误@差的损失函数或者代价函数的，而且我们希望损失函数越小越好。由这两个矛@盾，我们不妨让代价函数为上述组合对数函数的相反数：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K\left[y_k^{(i)}\log h_{\theta }{\left(x^{(i)}\right)}_k+\left(1-y_k^{(i)}\right)\log \left(1-h_{\theta }{\left(x^{(i)}\right)}_k\right)\right]$$
此式即为从最大似然角度来形成的交叉熵代价函数。

交叉熵代价函数的另一种推导：

$$\begin{array}{rl}\frac{\partial L}{\partial b}& =\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}\frac{\partial z}{\partial b}\\ & =\frac{\partial L}{\partial a}{\delta }^{\prime }(z)\frac{\partial (wx+b)}{\partial b}\\ & =\frac{\partial L}{\partial a}{\delta }^{\prime }(z)\\ & =\frac{\partial L}{\partial a}a(1-a)\end{array}$$

$$由({\delta }^{\prime }(z)=\delta (z)(1-\delta (z)))$$
而在均方误差代价函数中推导的b梯度公式为：
$$\frac{\partial L}{\partial b}=(a-y){\delta }^{\prime }(z)$$
为了消掉该公式中的${\delta }^{\prime }(z)$ ,我们想找到一个代价函数使得：
$$\frac{\partial L}{\partial b}=(a-y)$$
即为：
$$\frac{\partial L}{\partial a}a(1-a)=(a-y)$$
对偏微分方程求解，可得：
$$L=-[y\ln a+(1-a)\ln (1-a)]+\text{constant }$$
即为交叉熵代价函数。

[参考文档]
1、统计学习方法
2、机器学习与神经网络（机械工业出版社）