向然学习资料网为同学们提供北京大学高等代数第3版下册考试题库
北京大学数学系《高等代数》(第3版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(下册)

课程目录
第一部分 名校考研真题
第6章 线性空间
第7章 线性变换
第8章 λ-矩阵
第9章 欧几里得空间
第10章 双线性函数与辛空间
第二部分 课后习题
第6章 线性空间
第7章 线性变换
第8章 λ-矩阵*
第9章 欧几里得空间
第10章 双线性函数与辛空间
第三部分 章节题库
第6章 线性空间
第7章 线性变换
第8章 λ-矩阵
第9章 欧几里得空间
第10章 双线性函数与辛空间
第四部分 模拟试题
北京大学数学系《高等代数》(第3版)配套模拟试题及详解
课程简介
本书是详解研究生入学考试指定考研参考书目为北京大学数学系《高等代数》的配套题库,包括名校考研真题、课后习题、章节题库和模拟试题四大部分。为了方便题库上线和读者阅读,本题库分上、下两册,每章包括以下四部分:
第一部分为名校考研真题及详解。本部分从指定北京大学数学系编写的《高等代数》(第3版)为考研参考书目的名校历年考研真题中挑选具有代表性的部分,并对其进行了详细的解答。所选考研真题既注重对基础知识的掌握,让学员具有扎实的专业基础;又对一些重难点部分(包括教材中未涉及到的知识点)进行详细阐释,以使学员不遗漏任何一个重要知识点。
第二部分为课后习题及详解。本部分对北京大学数学系编写的《高等代数》(第3版)教材每一章的课后习题进行了详细的分析和解答,并对个别知识点进行了扩展。课后习题答案经过多次修改,质量上乘,特别适合应试作答和临考冲刺。
第三部分为章节题库及详解。本部分严格按照北京大学数学系编写的《高等代数》(第3版)教材内容进行编写,每一章都精心挑选经典常见考题,并予以详细解答。熟练掌握本书考题的解答,有助于学员理解和掌握有关概念、原理,并提高解题能力。
第四部分为模拟试题及详解。参照北京大学数学系编写的《高等代数》(第3版)教材,根据各高校历年考研真题的命题规律及热门考点精心编写了1套考前模拟试题,并提供详尽的解答。通过模拟试题的练习,学员既可以用来检测学习该考试科目的效果,又可以用来评估对自己的应试能力。
本书提供电子书及纸质书,方便对照复习。
【试读部分内容】
第一部分 名校考研真题
第6章 线性空间
一、选择题
1.下面哪一种变换是线性变换( ).[西北工业大学研]
A.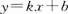 B.
B.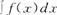 C.
C.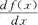
【答案】C查看答案
【解析】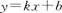 不一定是线性变换,比如
不一定是线性变换,比如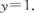 则
则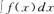 也不是线性变换,比如给
也不是线性变换,比如给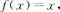 而
而 不是惟一的.
不是惟一的.
2.在n维向量空间取出两个向量组,它们的秩( ).[西北工业大学研]
A.必相等 B.可能相等亦可能不相等 C.不相等
【答案】B查看答案
【解析】比如在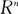 中选三个向量组
中选三个向量组
(I):0
(Ⅱ)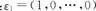
(Ⅲ)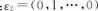 .
.
若选(I)(II),秩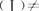 秩(II),从而否定A,若选(Ⅱ)(Ⅲ),秩(Ⅲ)=秩(Ⅱ),从而否定C,故选B.
秩(II),从而否定A,若选(Ⅱ)(Ⅲ),秩(Ⅲ)=秩(Ⅱ),从而否定C,故选B.
二、填空题
1.若
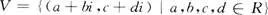
则V对于通常的加法和数乘,在复数域C上是______维的,而在实数域R上是______维的.[中国人民大学研]
【答案】2;4.查看答案
【解析】在复数域上令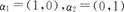 ;则
;则 是线性无关的.
是线性无关的.
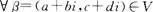
则
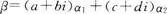
此即证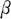 可由
可由 线性表出.
线性表出.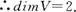
在实数域上,令
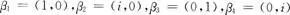
若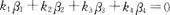 ,其中
,其中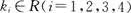 ,则
,则
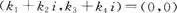
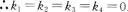 此即
此即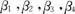 在R上线性关.
在R上线性关.
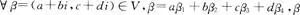 可由
可由 线性表出,所以在实数域R上,有
线性表出,所以在实数域R上,有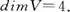
三、分析计算题
1.设V是复数域上n维线性空间,V1和V2各为V的r1维和r2维子空间,试求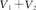 之维数的一切可能值.[南京大学研]
之维数的一切可能值.[南京大学研]
解:取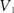 的一组基
的一组基 ,再取
,再取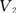 的一组基
的一组基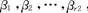 则
则
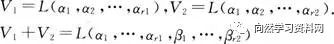
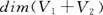 =秩
=秩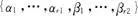
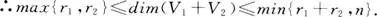
2.设U是由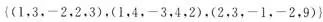 生成的
生成的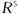 的子空间,W是由
的子空间,W是由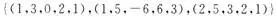 生成的
生成的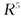 的子空间,求
的子空间,求
(1)U+W:
(2)L∩W的维数与基底.[同济大学研]
解:(1)令
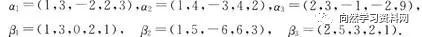
可得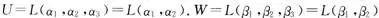 .所以
.所以
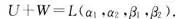
由于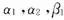 为
为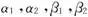 的一个极大线性无关组,因此又可得
的一个极大线性无关组,因此又可得
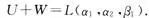
且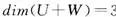 ,故
,故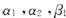 为U+W的一组基.
为U+W的一组基.
(2)令
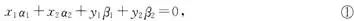
因为秩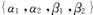 =3.所以齐次方程组①的基础解系由一个向量组成:
=3.所以齐次方程组①的基础解系由一个向量组成:
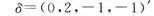
再令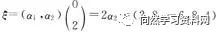 ,则
,则
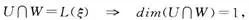
故ζ为U∩W的一组基.
3.设A是数域K上的一个m×n,矩阵,B是一个m维非零列向量.令
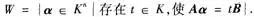
(1)证明:W关于Kn的运算构成Kn的一个子空间;
(2)设线性方程组AX=B的增广矩阵的秩为r.证明W的维数dimW=n-r+1:
(3)对于非齐次线性方程组
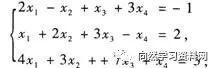
求W的一个基.[华东师范大学研]
证明:(1)显然W≠ ,又
,又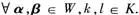
因为存在t1,t2使Aα=t1B,Aβ=t2B.所以
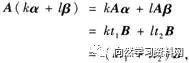
即kα+lβ∈W,此说明W是Kn的子空间.
(2)对线性方程组(A,B)Xn+1=0,由题设,其解空间V的维数为(n+1)-r(A,B)=n-r+1.
任取α∈W,存在t∈K,使
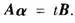
所以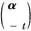 是线性方程组(A,B)Xn+1=0的解.
是线性方程组(A,B)Xn+1=0的解.
相关资料推荐:北京大学数学系《高等代数》(第3版)网授精讲班【教材精讲+考研真题串讲】
向然学习资料网:xrxxzlw
为您提供优质资料助你顺利通关!

免费试看/下载:








 这是一份详细解读北京大学数学系《高等代数》(第3版)下册的考试题库,包含名校考研真题、课后习题、章节题库和模拟试题,覆盖线性空间、线性变换、λ-矩阵等核心章节,旨在帮助学生全面掌握高等代数知识。
这是一份详细解读北京大学数学系《高等代数》(第3版)下册的考试题库,包含名校考研真题、课后习题、章节题库和模拟试题,覆盖线性空间、线性变换、λ-矩阵等核心章节,旨在帮助学生全面掌握高等代数知识。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








