655-输出二叉树
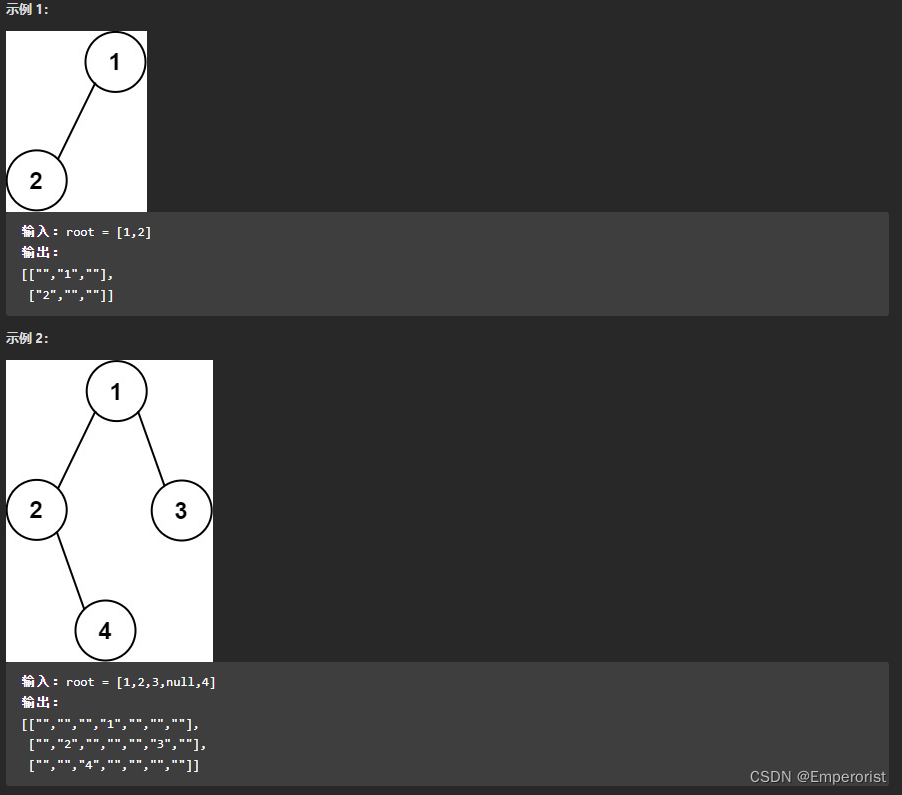
给你一棵二叉树的根节点 root ,请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ,用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则:
树的 高度 为 height ,矩阵的行数 m 应该等于 height + 1 。
矩阵的列数 n 应该等于 2height+1 - 1 。
根节点 需要放置在 顶行 的 正中间 ,对应位置为 res[0][(n-1)/2] 。
对于放置在矩阵中的每个节点,设对应位置为 res[r][c] ,将其左子节点放置在 res[r+1][c-2height-r-1] ,右子节点放置在 res[r+1][c+2height-r-1] 。
继续这一过程,直到树中的所有节点都妥善放置。
任意空单元格都应该包含空字符串 “” 。
返回构造得到的矩阵 res 。
方法一:深度优先搜索
思路与算法
我们可以通过深度优先搜索来解决此题。首先通过深度优先搜索来得到二叉树的高度height(注意高度从 0 开始),然后创建一个行数为 m=height+1,列数为 n=2^(height+1) −1 的答案数组res 放置节点的值(字符串形式)。根节点的值应当放在当前空间的第一行正中间。根节点所在的行与列会将剩余空间划分为两部分(左下部分和右下部分),然后递归地将左子树输出在左下部分空间,右子树输出在右下部分空间即可。
class Solution {
public:
int calDepth(TreeNode* root) {
int h = 0;
if (root->left) {
h = max(h, calDepth(root->left) + 1);
}
if (root->right) {
h = max(h, calDepth(root->right) + 1);
}
return h;
}
void dfs(vector<vector<string>>& res, TreeNode* root, int r, int c, const int& height) {
res[r][c] = to_string(root->val);
if (root->left) {
dfs(res, root->left, r + 1, c - (1 << (height - r - 1)), height);
}
if (root->right) {
dfs(res, root->right, r + 1, c + (1 << (height - r - 1)), height);
}
}
vector<vector<string>> printTree(TreeNode* root) {
int height = calDepth(root);
int m = height + 1;
int n = (1 << (height + 1)) - 1;
vector<vector<string>> res(m, vector<string>(n, ""));
dfs(res, root, 0, (n - 1) / 2, height);
return res;
}
};
class Solution:
def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
def calDepth(node: Optional[TreeNode]) -> int:
return max(calDepth(node.left) + 1 if node.left else 0, calDepth(node.right) + 1 if node.right else 0)
height = calDepth(root)
m = height + 1
n = 2 ** m - 1
ans = [[''] * n for _ in range(m)]
def dfs(node: Optional[TreeNode], r: int, c: int) -> None:
ans[r][c] = str(node.val)
if node.left:
dfs(node.left, r + 1, c - 2 ** (height - r - 1))
if node.right:
dfs(node.right, r + 1, c + 2 ** (height - r - 1))
dfs(root, 0, (n - 1) // 2)
return ans
- 时间复杂度:O(height×2^height ),其中height 是二叉树的高度。需要填充 (height+1)×(2^(height+1) −1) 的数组。
- 空间复杂度:O(height),其中height 是二叉树的高度。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度。注意返回值不计入空间复杂度。
方法二:广度优先搜索
思路与算法
我们也可以通过广度优先搜索来解决此题。首先通过广度优先搜索来得到二叉树的高度height,然后创建一个行数为m=height+1,列数为 n=2^(height+1)−1 的答案数组 res 放置节点的值(字符串形式)。使用广度优先搜索遍历每一个节点时,记录每一个节点对应的放置空间,每一个节点的值放置在对应空间的第一行正中间,然后其所在的行和列会将剩余空间划分为两部分(左下部分和右下部分),并把它的非空左子节点和非空右子节点以及它们的对应的放置空间放入队列即可。特别地,根节点的放置空间为整个 res 数组。
class Solution {
public:
int calDepth(TreeNode* root) {
int res = -1;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int len = q.size();
res++;
while (len) {
len--;
auto t = q.front();
q.pop();
if (t->left) {
q.push(t->left);
}
if (t->right) {
q.push(t->right);
}
}
}
return res;
}
vector<vector<string>> printTree(TreeNode* root) {
int height = calDepth(root);
int m = height + 1;
int n = (1 << (height + 1)) - 1;
vector<vector<string>> res(m, vector<string>(n, ""));
queue<tuple<TreeNode*, int, int>> q;
q.push({root, 0, (n - 1) / 2});
while (!q.empty()) {
auto t = q.front();
q.pop();
int r = get<1>(t), c = get<2>(t);
res[r][c] = to_string(get<0>(t)->val);
if (get<0>(t)->left) {
q.push({get<0>(t)->left, r + 1, c - (1 << (height - r - 1))});
}
if (get<0>(t)->right) {
q.push({get<0>(t)->right, r + 1, c + (1 << (height - r - 1))});
}
}
return res;
}
};
class Solution:
def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
def calDepth(root: Optional[TreeNode]) -> int:
h = -1
q = [root]
while q:
h += 1
tmp = q
q = []
for node in tmp:
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
return h
height = calDepth(root)
m = height + 1
n = 2 ** m - 1
ans = [[''] * n for _ in range(m)]
q = deque([(root, 0, (n - 1) // 2)])
while q:
node, r, c = q.popleft()
ans[r][c] = str(node.val)
if node.left:
q.append((node.left, r + 1, c - 2 ** (height - r - 1)))
if node.right:
q.append((node.right, r + 1, c + 2 ** (height - r - 1)))
return ans
时间复杂度和空间复杂度同方法一
654-最大二叉树
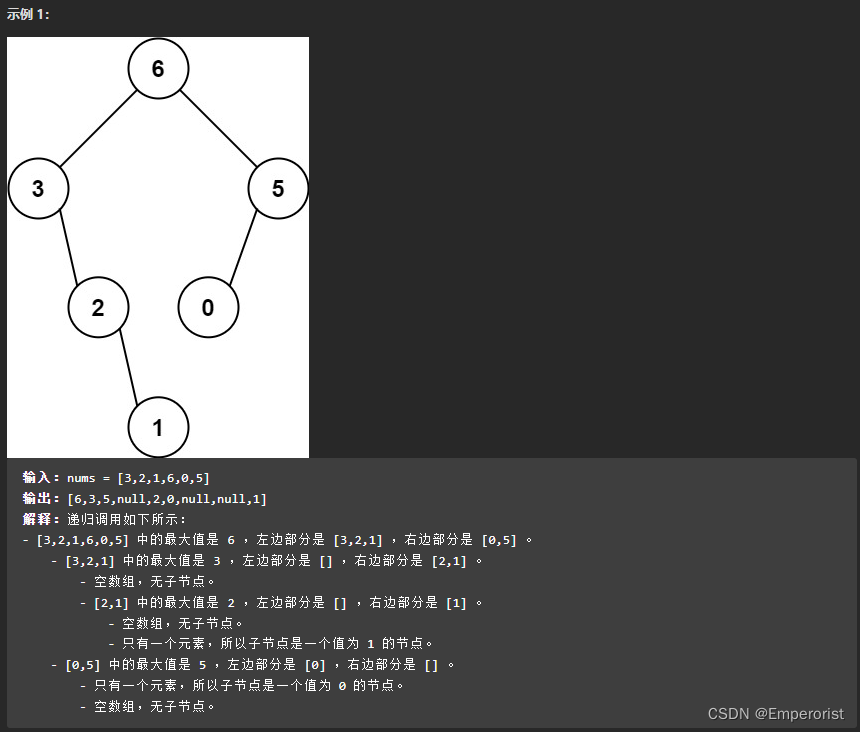
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
方法一:深度优先搜索
使用递归的方法:
首先寻找数组中的最大值,构造根节点;
寻找根节点左子数组的最大值,构造根节点的左儿子;不断递归
寻找根节点右子数组的最大值,构造根节点的右儿子;不断递归
递归截止条件为数组为空,返回nullptr
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.empty())
return nullptr;
int index=IndexMax(nums);
TreeNode *node=new TreeNode(nums[index]);
vector<int>num;
num.assign(nums.begin(), nums.begin()+index );
node->left = constructMaximumBinaryTree(num);
num.assign(nums.begin() + index + 1, nums.end());
node->right = constructMaximumBinaryTree(num);
return node;
}
int IndexMax(vector<int>nums)
{
int n=nums.size(),value=0,index=0;
for(int i=0;i<n;++i)
{
if(nums[i]>value)
{
index=i;
value=nums[i];
}
}
return index;
}
};
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
def construct(left: int, right: int) -> Optional[TreeNode]:
if left > right:
return None
best = left
for i in range(left + 1, right + 1):
if nums[i] > nums[best]:
best = i
node = TreeNode(nums[best])
node.left = construct(left, best - 1)
node.right = construct(best + 1, right)
return node
return construct(0, len(nums) - 1)
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
632-在二叉树中增加一行
给定一个二叉树的根 root 和两个整数 val 和 depth ,在给定的深度 depth 处添加一个值为 val 的节点行。
注意,根节点 root 位于深度 1 。
加法规则如下:
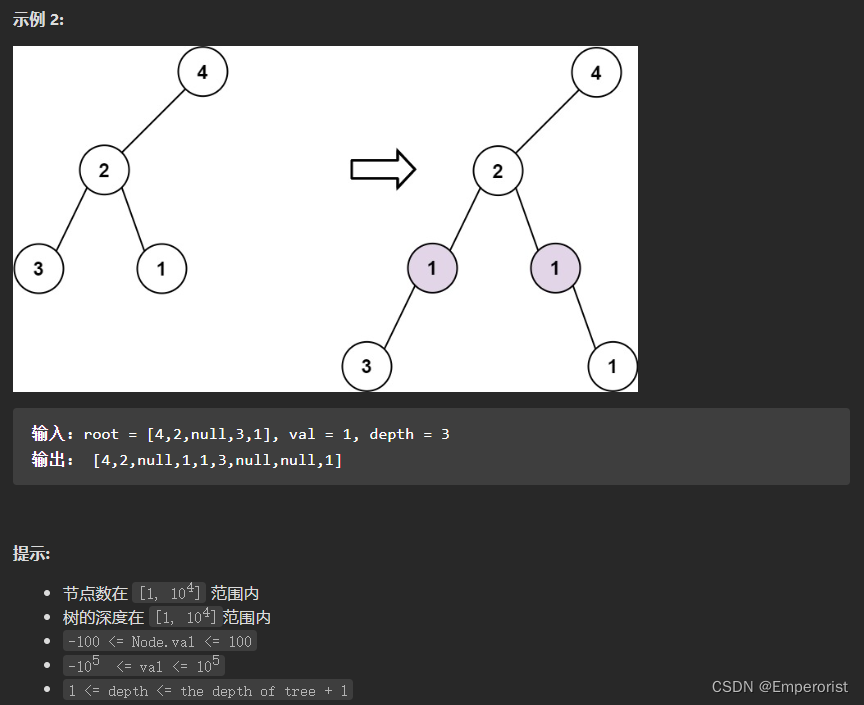
给定整数 depth,对于深度为 depth - 1 的每个非空树节点 cur ,创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
cur 原来的左子树应该是新的左子树根的左子树。
cur 原来的右子树应该是新的右子树根的右子树。
如果 depth == 1 意味着 depth - 1 根本没有深度,那么创建一个树节点,值 val 作为整个原始树的新根,而原始树就是新根的左子树。
方法一:深度优先搜索
思路
当输入depth 为 1 时,需要创建一个新的 root,并将原 root 作为新 root 的左子节点。当depth 为 2 时,需要在 root 下新增两个节点left 和 right 作为root 的新子节点,并把原左子节点作为left 的左子节点,把原右子节点作为 right 的右子节点。当 depth 大于 2 时,需要继续递归往下层搜索,并将depth 减去 1,直到搜索到 depth 为 2。
class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
if (root == nullptr) {
return nullptr;
}
if (depth == 1) {
return new TreeNode(val, root, nullptr);
}
if (depth == 2) {
root->left = new TreeNode(val, root->left, nullptr);
root->right = new TreeNode(val, nullptr, root->right);
} else {
root->left = addOneRow(root->left, val, depth - 1);
root->right = addOneRow(root->right, val, depth - 1);
}
return root;
}
};
class Solution:
def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:
if root == None:
return
if depth == 1:
return TreeNode(val, root, None)
if depth == 2:
root.left = TreeNode(val, root.left, None)
root.right = TreeNode(val, None, root.right)
else:
root.left = self.addOneRow(root.left, val, depth - 1)
root.right = self.addOneRow(root.right, val, depth - 1)
return root
- 时间复杂度:O(n),其中 n 为输入的树的节点数。最坏情况下,需要遍历整棵树。
- 空间复杂度:O(n),递归的深度最多为 O(n)。
606-根据二叉树创建字符串
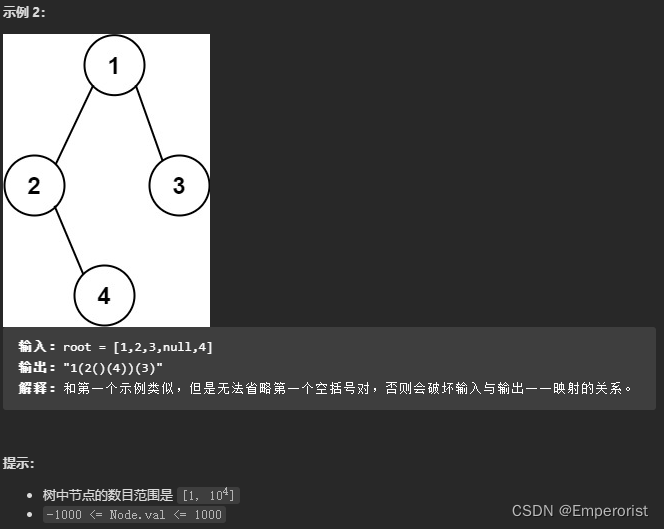
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 “()” 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
方法一:递归
我们可以使用递归的方法得到二叉树的前序遍历,并在递归时加上额外的括号。
会有以下 4 种情况:
如果当前节点有两个孩子,那我们在递归时,需要在两个孩子的结果外都加上一层括号;
如果当前节点没有孩子,那我们不需要在节点后面加上任何括号;
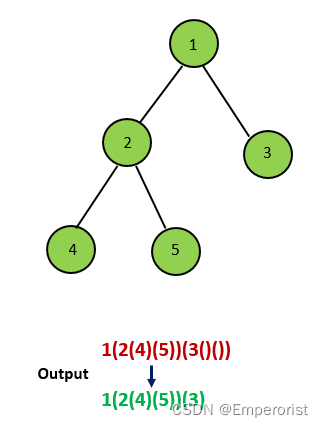
如果当前节点只有左孩子,那我们在递归时,只需要在左孩子的结果外加上一层括号,而不需要给右孩子加上任何括号;
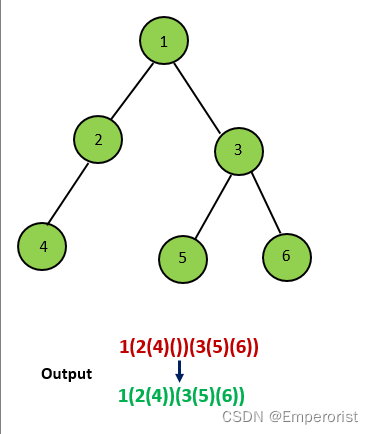
如果当前节点只有右孩子,那我们在递归时,需要先加上一层空的括号 ‘()’ 表示左孩子为空,再对右孩子进行递归,并在结果外加上一层括号。
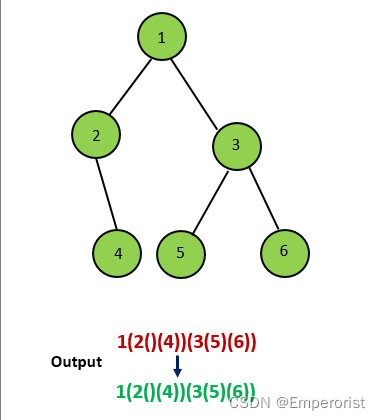
class Solution {
public:
string tree2str(TreeNode *root) {
if (root == nullptr) {
return "";
}
if (root->left == nullptr && root->right == nullptr) {
return to_string(root->val);
}
if (root->right == nullptr) {
return to_string(root->val) + "(" + tree2str(root->left) + ")";
}
return to_string(root->val) + "(" + tree2str(root->left) + ")(" + tree2str(root->right) + ")";
}
};
class Solution:
def tree2str(self, root: Optional[TreeNode]) -> str:
if root is None:
return ""
if root.left is None and root.right is None:
return str(root.val)
if root.right is None:
return f"{root.val}({self.tree2str(root.left)})"
return f"{root.val}({self.tree2str(root.left)})({self.tree2str(root.right)})"
- 时间复杂度:O(n),其中 n 是二叉树中的节点数目。
- 空间复杂度:O(n)。在最坏情况下会递归 n 层,需要 O(n) 的栈空间。
331-验证二叉树的前序序列化
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
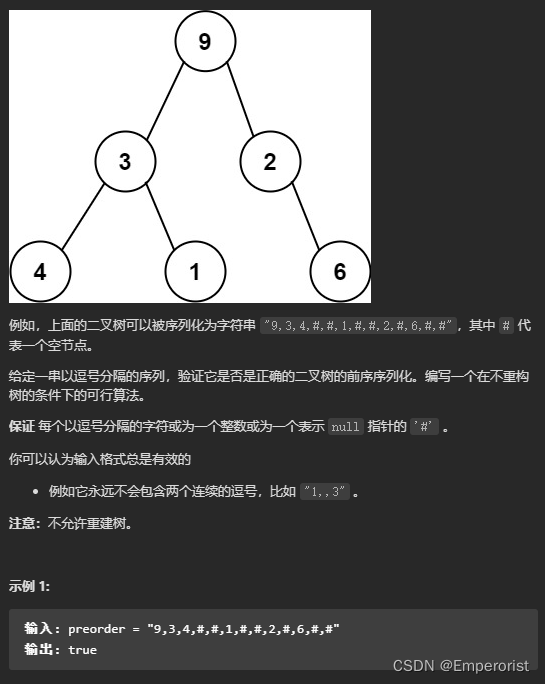
方法一:栈
我们可以定义一个概念,叫做槽位。一个槽位可以被看作「当前二叉树中正在等待被节点填充」的那些位置。
二叉树的建立也伴随着槽位数量的变化。每当遇到一个节点时:
如果遇到了空节点,则要消耗一个槽位;
如果遇到了非空节点,则除了消耗一个槽位外,还要再补充两个槽位。
此外,还需要将根节点作为特殊情况处理。

我们使用栈来维护槽位的变化。栈中的每个元素,代表了对应节点处剩余槽位的数量,而栈顶元素就对应着下一步可用的槽位数量。当遇到空节点时,仅将栈顶元素减 1;当遇到非空节点时,将栈顶元素减 1 后,再向栈中压入一个 2。无论何时,如果栈顶元素变为 0,就立刻将栈顶弹出。
遍历结束后,若栈为空,说明没有待填充的槽位,因此是一个合法序列;否则若栈不为空,则序列不合法。此外,在遍历的过程中,若槽位数量不足,则序列不合法。
class Solution {
public:
bool isValidSerialization(string preorder) {
int n = preorder.length();
int i = 0;
stack<int> stk;
stk.push(1);
while (i < n) {
if (stk.empty()) {
return false;
}
if (preorder[i] == ',') {
i++;
} else if (preorder[i] == '#'){
stk.top() -= 1;
if (stk.top() == 0) {
stk.pop();
}
i++;
} else {
// 读一个数字
while (i < n && preorder[i] != ',') {
i++;
}
stk.top() -= 1;
if (stk.top() == 0) {
stk.pop();
}
stk.push(2);
}
}
return stk.empty();
}
};
- 时间复杂度:O(n),其中 n 为字符串的长度。我们每个字符只遍历一次,同时每个字符对应的操作都是常数时间的。
- 空间复杂度:O(n)。此为栈所需要使用的空间。
方法二:前序遍历
class Solution {
public:
int n;
bool dfs(string& s, int& pos){ //dfs递归按前序顺序(根左右)建树
if(pos >= n) return false; //递归有两个出口,越界返回false, s[pos] =='#'代表空节点,自然为true
if(s[pos] == '#'){
pos += 2; //因为有逗号,故应加2
return true;
}
while(pos < n && isdigit(s[pos])) pos++; //对当前节点访问只需要读数移动pos即可
pos++; //同样跳过逗号
if(!dfs(s, pos)) return false; //对左右节点dfs建树,若有任意节点建树不成功,则代表整个序列不合法
if(!dfs(s, pos)) return false;
return true;
}
bool isValidSerialization(string preorder) {
n = preorder.size();
int pos = 0;
return dfs(preorder, pos) && pos >= n; //成功建树且序列无多余节点才算合格
}
};
563-二叉树的 坡度
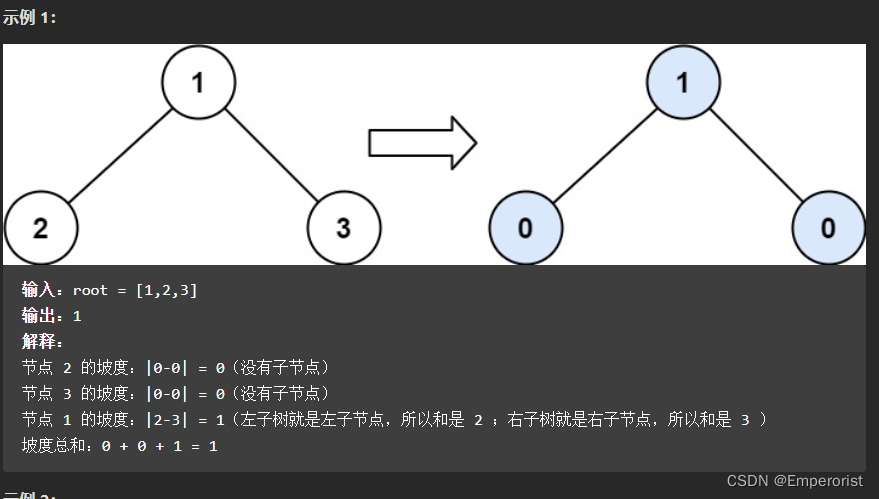
给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
深度优先搜索
根据题意,我们需要累计二叉树中所有结点的左子树结点之和与右子树结点之和的差的绝对值。因此,我们可以使用深度优先搜索,在遍历每个结点时,累加其左子树结点之和与右子树结点之和的差的绝对值,并返回以其为根结点的树的结点之和。
具体地,我们实现算法如下:
从根结点开始遍历,设当前遍历的结点为node;
遍历node 的左子结点,得到左子树结点之和sum_left;遍历 node 的右子结点,得到右子树结点之和 sum_right;
将左子树结点之和与右子树结点之和的差的绝对值累加到结果变量ans;
返回以node 作为根结点的树的结点之和 sum_left+sum_right+node.val。
class Solution {
public:
int ans = 0;
int findTilt(TreeNode* root) {
dfs(root);
return ans;
}
int dfs(TreeNode* node) {
if (node == nullptr) {
return 0;
}
int sumLeft = dfs(node->left);
int sumRight = dfs(node->right);
ans += abs(sumLeft - sumRight);
return sumLeft + sumRight + node->val;
}
};
class Solution:
def __init__(self):
self.ans = 0
def findTilt(self, root: TreeNode) -> int:
self.dfs(root)
return self.ans
def dfs(self, node):
if not node:
return 0
sum_left = self.dfs(node.left)
sum_right = self.dfs(node.right)
self.ans += abs(sum_left - sum_right)
return sum_left + sum_right + node.val
- 时间复杂度:O(n),其中 n 为二叉树中结点总数。我们需要遍历每一个结点。
- 空间复杂度:O(n)。在最坏情况下, 当树为线性二叉树(即所有结点都只有左子结点或没有结点)时,树的高度为 n−1,在递归时我们需要存储 n 个结点。
257-二叉树的所有路径
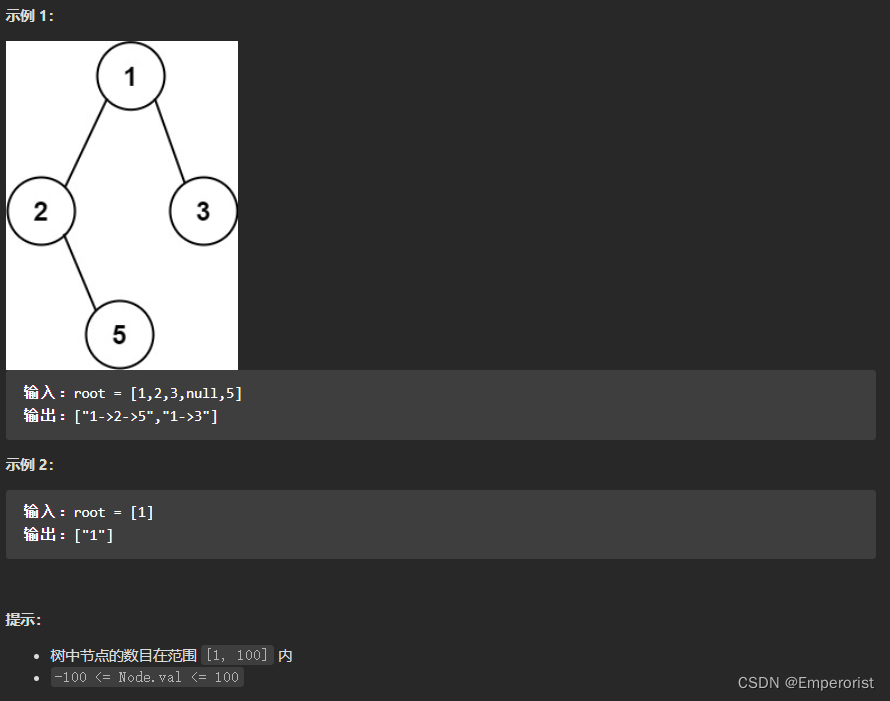
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
方法一:深度优先搜索
最直观的方法是使用深度优先搜索。在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。
如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
class Solution {
public:
void construct_paths(TreeNode* root, string path, vector<string>& paths) {
if (root != nullptr) {
path += to_string(root->val);
if (root->left == nullptr && root->right == nullptr) { // 当前节点是叶子节点
paths.push_back(path); // 把路径加入到答案中
} else {
path += "->"; // 当前节点不是叶子节点,继续递归遍历
construct_paths(root->left, path, paths);
construct_paths(root->right, path, paths);
}
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> paths;
construct_paths(root, "", paths);//“”处不能传入字符串的引用
return paths;
}
};
class Solution:
def binaryTreePaths(self, root):
"""
:type root: TreeNode
:rtype: List[str]
"""
def construct_paths(root, path):
if root:
path += str(root.val)
if not root.left and not root.right: # 当前节点是叶子节点
paths.append(path) # 把路径加入到答案中
else:
path += '->' # 当前节点不是叶子节点,继续递归遍历
construct_paths(root.left, path)
construct_paths(root.right, path)
paths = []
construct_paths(root, '')
return paths
- 时间复杂度:O(N^2),其中 N 表示节点数目。在深度优先搜索中每个节点会被访问一次且只会被访问一次,每一次会对 path 变量进行拷贝构造,时间代价为O(N),故时间复杂度为 O(N^2)。
- 空间复杂度:O(N^2),其中 N 表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。在最坏情况下,当二叉树中每个节点只有一个孩子节点时,即整棵二叉树呈一个链状,此时递归的层数为 N,此时每一层的 path 变量的空间代价的总和为 O(∑ i=1Ni)=O(N^2) 空间复杂度为 O(N^2)。最好情况下,当二叉树为平衡二叉树时,它的高度为logN,此时空间复杂度为 O((logN) ^2)。
方法二:广度优先搜索
我们也可以用广度优先搜索来实现。我们维护一个队列,存储节点以及根到该节点的路径。一开始这个队列里只有根节点。在每一步迭代中,我们取出队列中的首节点,如果它是叶子节点,则将它对应的路径加入到答案中。如果它不是叶子节点,则将它的所有孩子节点加入到队列的末尾。当队列为空时广度优先搜索结束,我们即能得到答案。
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> paths;
if (root == nullptr) {
return paths;
}
queue<TreeNode*> node_queue;
queue<string> path_queue;
node_queue.push(root);
path_queue.push(to_string(root->val));
while (!node_queue.empty()) {
TreeNode* node = node_queue.front();
string path = path_queue.front();//会把1->2一起取出来,不只是单个数,带箭头的
node_queue.pop();
path_queue.pop();
if (node->left == nullptr && node->right == nullptr) {
paths.push_back(path);
} else {
if (node->left != nullptr) {
node_queue.push(node->left);
path_queue.push(path + "->" + to_string(node->left->val));
}
if (node->right != nullptr) {
node_queue.push(node->right);
path_queue.push(path + "->" + to_string(node->right->val));
}
}
}
return paths;
}
};
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
paths = list()
if not root:
return paths
node_queue = collections.deque([root])
path_queue = collections.deque([str(root.val)])
while node_queue:
node = node_queue.popleft()
path = path_queue.popleft()
if not node.left and not node.right:
paths.append(path)
else:
if node.left:
node_queue.append(node.left)
path_queue.append(path + '->' + str(node.left.val))
if node.right:
node_queue.append(node.right)
path_queue.append(path + '->' + str(node.right.val))
return paths
- 时间复杂度:O(N^2),其中 N 表示节点数目。分析同方法一。
- 空间复杂度:O(N^2),其中 N 表示节点数目。在最坏情况下,队列中会存在 N 个节点,保存字符串的队列中每个节点的最大长度为 N,故空间复杂度为 O(N^2)。
199-二叉树的右视图
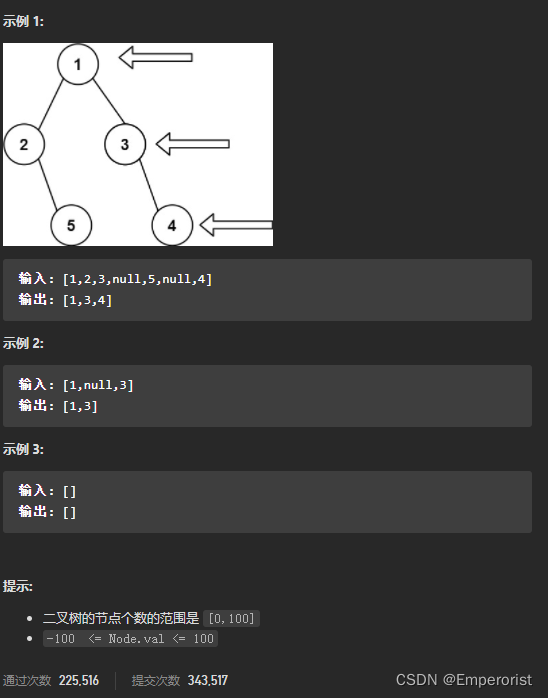
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
广度优先搜索
利用二叉树的层次遍历,右视图就是每一层的最后一个节点。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector <int> ret;
if (!root) {
return ret;
}
queue <TreeNode*> q;
q.push(root);
while (!q.empty()) {
int currentLevelSize = q.size();
for (int i = 1; i <= currentLevelSize; ++i) {
auto node = q.front(); q.pop();
if(i==currentLevelSize)
ret.push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
};
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
max_depth = -1
queue = deque([(root, 0)])
while queue:
node, depth = queue.popleft()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmost_value_at_depth[depth] = node.val
queue.append((node.left, depth + 1))
queue.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
- 时间复杂度 : O(n)。 每个节点最多进队列一次,出队列一次,因此广度优先搜索的复杂度为线性。
- 空间复杂度 : O(n)。每个节点最多进队列一次,所以队列长度最大不不超过 n,所以这里的空间代价为O(n)。
python中deque 数据类型来自于collections 模块,支持从头和尾部的常数时间 append/pop 操作。若使用 Python 的 list,通过 list.pop(0) 去除头部会消耗 O(n) 的时间。
226-二叉树翻转
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。

方法一:递归
/**
* 递归方式遍历反转
*/
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
- 时间复杂度:O(N),其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点,对每个节点而言,我们在常数时间内交换其两棵子树。
- 空间复杂度:O(N)。使用的空间由递归栈的深度决定,它等于当前节点在二叉树中的高度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)。
方法二:BFS、DFS
/**
* 层序遍历方式反转,从左到右遍历
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==nullptr)
return nullptr;
queue<TreeNode*>q;
q.push(root);
while(!q.empty())
{
TreeNode *node=q.front();
q.pop();
TreeNode*temp=node->left;
node->left=node->right;
node->right=temp;
if(node->left!=nullptr)
q.push(node->left);
if(node->right!=nullptr)
q.push(node->right);
}
return root;
}
};
/**
* 深度优先遍历的方式反转,,向下遍历
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==nullptr)
return nullptr;
stack<TreeNode*>stk;
stk.push(root);
while(!stk.empty())
{
int sz=stk.size();
for(int i=0;i<sz;++i)
{
TreeNode *node=stk.top();
stk.pop();
TreeNode*temp=node->left;
node->left=node->right;
node->right=temp;
if(node->left!=nullptr)
stk.push(node->left);
if(node->right!=nullptr)
stk.push(node->right);
}
}
return root;
}
};
时间复杂度和空间复杂度同上
116-填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。

方法一:递归
class Solution {
public:
Node* connect(Node* root) {
if(root==nullptr)
return nullptr;
helper(root->left,root->right);
return root;
}
void helper(Node*left1,Node*right1)
{
if(left1==nullptr||right1==nullptr)
return;
left1->next=right1;
helper(left1->left,left1->right); //左子树的左右指针
helper(right1->left,right1->right);//右子树的左右指针
helper(left1->right,right1->left); //左子树的右指针和左子树的左指针
}
};
方法二:层序遍历
题目本身希望我们将二叉树的每一层节点都连接起来形成一个链表。因此直观的做法我们可以对二叉树进行层次遍历,在层次遍历的过程中将我们将二叉树每一层的节点拿出来遍历并连接。
层次遍历基于广度优先搜索,它与广度优先搜索的不同之处在于,广度优先搜索每次只会取出一个节点来拓展,而层次遍历会每次将队列中的所有元素都拿出来拓展,这样能保证每次从队列中拿出来遍历的元素都是属于同一层的,因此我们可以在遍历的过程中修改每个节点的 next 指针,同时拓展下一层的新队列。
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr) {
return root;
}
// 初始化队列同时将第一层节点加入队列中,即根节点
queue<Node*> Q;
Q.push(root);
// 外层的 while 循环迭代的是层数
while (!Q.empty()) {
// 记录当前队列大小
int size = Q.size();
// 遍历这一层的所有节点
for(int i = 0; i < size; i++) {
// 从队首取出元素
Node* node = Q.front();
Q.pop();
// 连接
if (i < size - 1) {
node->next = Q.front();
}
// 拓展下一层节点
if (node->left != nullptr) {
Q.push(node->left);
}
if (node->right != nullptr) {
Q.push(node->right);
}
}
}
// 返回根节点
return root;
}
};
import collections
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
# 初始化队列同时将第一层节点加入队列中,即根节点
Q = collections.deque([root])
# 外层的 while 循环迭代的是层数
while Q:
# 记录当前队列大小
size = len(Q)
# 遍历这一层的所有节点
for i in range(size):
# 从队首取出元素
node = Q.popleft()
# 连接
if i < size - 1:
node.next = Q[0]
# 拓展下一层节点
if node.left:
Q.append(node.left)
if node.right:
Q.append(node.right)
# 返回根节点
return root
- 时间复杂度:O(N)。每个节点会被访问一次且只会被访问一次,即从队列中弹出,并建立next 指针。
- 空间复杂度:O(N)。这是一棵完美二叉树,它的最后一个层级包含N/2 个节点。广度优先遍历的复杂度取决于一个层级上的最大元素数量。这种情况下空间复杂度为 O(N)。
方法三::使用已建立的next 指针
思路:
一棵树中,存在两种类型的next指针。
1.第一种情况是连接同一个父节点的两个子节点。它们可以通过同一个节点直接访问到,因此执行下面操作即可完成连接。
node.left.next = node.right
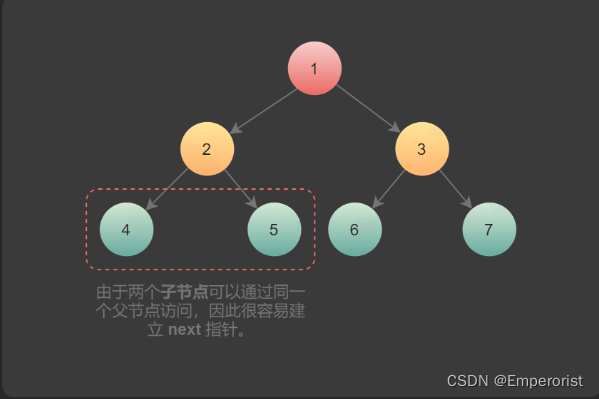
2.第二种情况在不同父亲的子节点之间建立连接,这种情况不能直接连接。
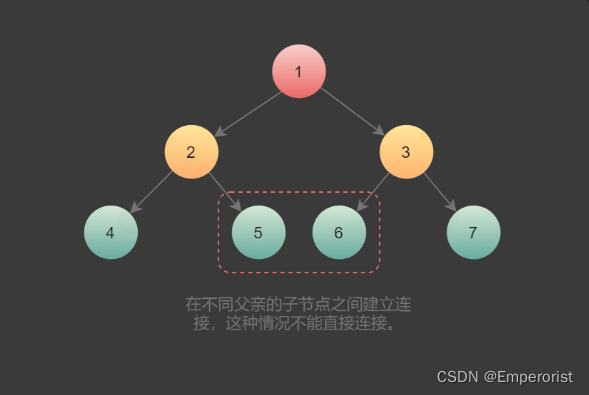
如果每个节点有指向父节点的指针,可以通过该指针找到next 节点。如果不存在该指针,则按照下面思路建立连接:
第 N 层节点之间建立 next 指针后,再建立第 N+1 层节点的next 指针。可以通过 next 指针访问同一层的所有节点,因此可以使用第 N 层的 next 指针,为第 N+1 层节点建立next 指针。
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr) {
return root;
}
// 从根节点开始
Node* leftmost = root;
while (leftmost->left != nullptr) {
// 遍历这一层节点组织成的链表,为下一层的节点更新 next 指针
Node* head = leftmost;
while (head != nullptr) {
// CONNECTION 1
head->left->next = head->right;
// CONNECTION 2
if (head->next != nullptr) {
head->right->next = head->next->left;
}
// 指针向后移动
head = head->next;
}
// 去下一层的最左的节点
leftmost = leftmost->left;
}
return root;
}
};
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
# 从根节点开始
leftmost = root
while leftmost.left:
# 遍历这一层节点组织成的链表,为下一层的节点更新 next 指针
head = leftmost
while head:
# CONNECTION 1
head.left.next = head.right
# CONNECTION 2
if head.next:
head.right.next = head.next.left
# 指针向后移动
head = head.next
# 去下一层的最左的节点
leftmost = leftmost.left
return root
- 时间复杂度:O(N),每个节点只访问一次。
- 空间复杂度:O(1),不需要存储额外的节点。
617-合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。

方法一:深度优先遍历
可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树,并将对应的节点进行合并。
两个二叉树的对应节点可能存在以下三种情况,对于每种情况使用不同的合并方式。
如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,此时需要显性合并两个节点。
对一个节点进行合并之后,还要对该节点的左右子树分别进行合并。这是一个递归的过程。
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == nullptr) {
return t2;
}
if (t2 == nullptr) {
return t1;
}
auto merged = new TreeNode(t1->val + t2->val);
merged->left = mergeTrees(t1->left, t2->left);
merged->right = mergeTrees(t1->right, t2->right);
return merged;
}
};
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if not t1:
return t2
if not t2:
return t1
merged = TreeNode(t1.val + t2.val)
merged.left = self.mergeTrees(t1.left, t2.left)
merged.right = self.mergeTrees(t1.right, t2.right)
return merged
- 时间复杂度:O(min(M,N)),其中 M 和 N 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索,只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作,因此被访问到的节点数不会超过较小的二叉树的节点数。
- 空间复杂度:O(min(M,N)),其中M 和N 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数,递归调用的层数不会超过较小的二叉树的最大高度,最坏情况下,二叉树的高度等于节点数。
236-二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”

方法一:递归
我们递归遍历整棵二叉树,定义 fx
表示 x节点的子树中是否包含 p 节点或 q 节点,如果包含为 true,否则为 false。那么符合条件的最近公共祖先 x 一定满足如下条件:
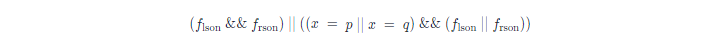
其中lson 和rson 分别代表 x 节点的左孩子和右孩子。初看可能会感觉条件判断有点复杂,我们来一条条看,flson && frson说明左子树和右子树均包含 p 节点或 q 节点,如果左子树包含的是 p节点,那么右子树只能包含 q 节点,反之亦然,因为 p 节点和 q 节点都是不同且唯一的节点,因此如果满足这个判断条件即可说明 x 就是我们要找的最近公共祖先。再来看第二条判断条件,这个判断条件即是考虑了 x 恰好是 p 节点或 q 节点且它的左子树或右子树有一个包含了另一个节点的情况,因此如果满足这个判断条件亦可说明 x 就是我们要找的最近公共祖先。
下图展示了一个示例,搜索树中两个节点 9 和 11 的最近公共祖先。

class Solution {
public:
TreeNode* ans;
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr) return false;
bool lson = dfs(root->left, p, q);
bool rson = dfs(root->right, p, q);
if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {
ans = root;
}
return lson || rson || (root->val == p->val || root->val == q->val);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root, p, q);
return ans;
}
};
- 时间复杂度:O(N),其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次,因此时间复杂度为 O(N)。
- 空间复杂度:O(N) ,其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度,二叉树最坏情况下为一条链,此时高度为 N,因此空间复杂度为 O(N)。
方法二:存储父节点
我们可以用哈希表存储所有节点的父节点,然后我们就可以利用节点的父节点信息从 p 结点开始不断往上跳,并记录已经访问过的节点,再从 q 节点开始不断往上跳,如果碰到已经访问过的节点,那么这个节点就是我们要找的最近公共祖先。
算法
从根节点开始遍历整棵二叉树,用哈希表记录每个节点的父节点指针。
从 p 节点开始不断往它的祖先移动,并用数据结构记录已经访问过的祖先节点。
同样,我们再从 q 节点开始不断往它的祖先移动,如果有祖先已经被访问过,即意味着这是 p 和 q 的深度最深的公共祖先,即 LCA 节点。
class Solution {
public:
unordered_map<int, TreeNode*> fa;
unordered_map<int, bool> vis;
void dfs(TreeNode* root){
if (root->left != nullptr) {
fa[root->left->val] = root;
dfs(root->left);
}
if (root->right != nullptr) {
fa[root->right->val] = root;
dfs(root->right);
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
fa[root->val] = nullptr;
dfs(root);
while (p != nullptr) {
vis[p->val] = true;
p = fa[p->val];
}
while (q != nullptr) {
if (vis[q->val]) return q;
q = fa[q->val];
}
return nullptr;
}
};
- 时间复杂度:O(N)
- 空间复杂度:O(N)
100-相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
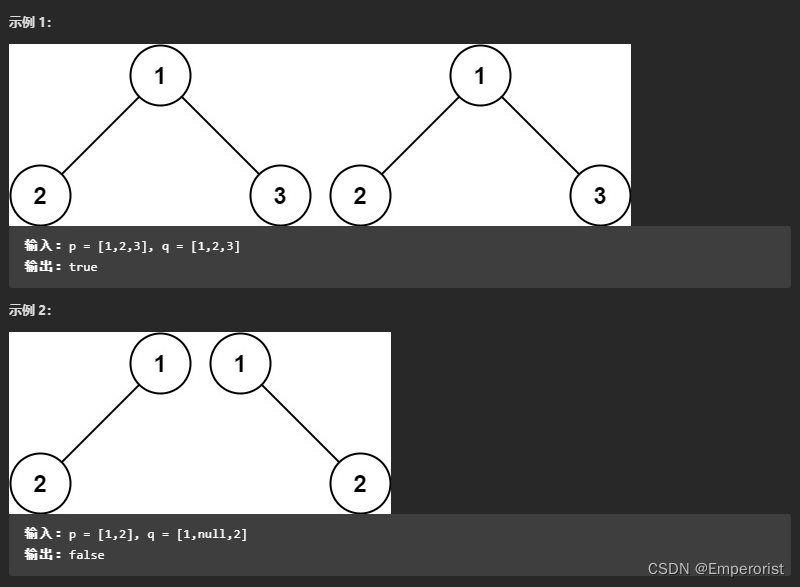
方法一:深度优先遍历
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(p==nullptr||q==nullptr) return p==q;
if(p->val!=q->val) return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
};
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q:
return True
elif not p or not q:
return False
elif p.val != q.val:
return False
else:
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
- 时间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行深度优先搜索,只有当两个二叉树中的对应节点都不为空时才会访问到该节点,因此被访问到的节点数不会超过较小的二叉树的节点数。
- 空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于递归调用的层数,递归调用的层数不会超过较小的二叉树的最大高度,最坏情况下,二叉树的高度等于节点数。
方法二:广度优先遍历
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr || q == nullptr) {
return p==q;
}
queue <TreeNode*> queue1, queue2;
queue1.push(p);
queue2.push(q);
while (!queue1.empty() && !queue2.empty()) {
auto node1 = queue1.front();
queue1.pop();
auto node2 = queue2.front();
queue2.pop();
if (node1->val != node2->val) {
return false;
}
auto left1 = node1->left, right1 = node1->right, left2 = node2->left, right2 = node2->right;
if ((left1 == nullptr) ^ (left2 == nullptr)) {
return false;
}
if ((right1 == nullptr) ^ (right2 == nullptr)) {
return false;
}
if (left1 != nullptr) {
queue1.push(left1);
}
if (right1 != nullptr) {
queue1.push(right1);
}
if (left2 != nullptr) {
queue2.push(left2);
}
if (right2 != nullptr) {
queue2.push(right2);
}
}
return queue1.empty() && queue2.empty();
}
};
- 时间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行广度优先搜索,只有当两个二叉树中的对应节点都不为空时才会访问到该节点,因此被访问到的节点数不会超过较小的二叉树的节点数。
- 空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于队列中的元素个数,队列中的元素个数不会超过较小的二叉树的节点数。






















 109
109











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








