《精密测量基础》综合实验报告
弓高弦长仪
学 院 精仪学院 专 业 测控技术与仪器
2019年12月1日
目 录
第一章 任务目标
设计一种大轴径（φ1000mm）测量的弓高弦长仪，给出方案设计图（结构示意图）和主要结构参数；画出原理图，分析测量原理，建立测量模型；根据测量模型讨论测量分辨力，分析测量误差源，评估目标测量不确定度。
第二章 弓高弦长仪的结构
“弓高弦长”法是分别对被测工件的一段圆弧的弦长和弓高进行测量,再通过公式计算间接得出被测圆直径的方法。该测量方法测量原理简单、测量范围大、操作简便。对于大直径工件,尤其是不完整圆工件或其他用直接测量法测量直径非常困难的工件进行检测,“弓高弦长”法是行之有效的常用方法。
对于大轴径（φ1000mm）测量，选择定弦长，求弓高的方式。在对测量直径进行标定时, 弓高弦长仪的2个测量头的中心距离为固定弦长, 而轴轮边缘处与测量头之间的高度差为弓高。具体操作过程为:在水平面的 3 个固定位置(测量仪两测量头及中间测轮下方)放置一定高度的量块, 改变测量仪中间7处或者两测量头下的量块的高度, 得到不同的高度差(弓高的变化)，以模拟出不同直径。
设计测量头的直径 d=30mm，两测量头间距为L=435.89mm，测量弓高为50mm。具体结构如图2.1。
图2.1 弓高弦长仪结构
第三章 弓高弦长法数学模型的建立与分析
3.1 弓高弦长法的数学模型
图3.1中的h为弓高,弦长为L(即测量仪的两支承圆柱的中心距),O为被测工件的理想圆心,O’为测量仪支承圆柱的圆心,被测工件的公称直径为D。测量仪器的结构方案为固定弦长L,测量弓高h。当测量外径时,被测工件的直径D由下式确定:
(D+d2)2=(L2)2+(D+d2-h)2
D=L24h+h-d
通过直接测量弓高h,而弦长L和支承轮直径d已知,带入式中便可算得被测圆的直径D。
3.2 弓高弦长法的误差分析
因为全部输入量彼此相互独立时,对式
D=L24h+h-d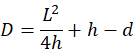
进行全微分,可得：
dD=∂D∂LdL+∂D∂hdh+∂D∂ddd=L2hdL+1-L24h2dh-dd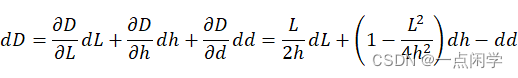
3.2.1 弦长L的误差
采用弓高弦长法测量被测工件的直径是一种间接测量，因此由公式uiy=∂f∂xiuxi
知，弦长L带来的不确定度分量为：
uLD=∂D∂LuL=L2huL
式中 uLD
为弓高带来的测量不确定度分量
D为被测工件直径
L为弦长的长度
uL
为L的标准不确定度
由上式可知, uLD
随着L的增大而增大,故应控制L的长度,以便减小L带来的误差。弓高h越小, uLD
越大。可见,弦长带来的系统误差uLD
对测量结果的影响是不容忽视的。在大直径测量仪中,该测量误差为不变的系统误差,是可以修正的,即在测量前先通过分段优化固定弦长的长度,测得实际值,求得uL
,并将其补偿到系统中,以满足系统的要求。
3.2.2 弓高h的误差
由公式uiy=∂f∂xiuxi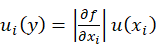
知，弓高h带来的不确定度分量为：
uhD=∂D∂huh=1-L24h2uh
由上式可知, uhD
随着L的减小而增大,故应尽可能增大L的长度,以便减小L带来的误差。弓高h越大,uhD
越大,弓高应尽可能控制在一定范围内。可见,弓高h带来的误差对测量结果的影响也是不容忽视的。同理,该测量误差也为不变的系统误差,是可以修正的,即在测量前,通过选取固定弦长的长度,求得uh
,并将其补偿到系统中,以满足系统的要求。
3.2.3 支承轮直径d的误差
由公式uiy=∂f∂xiuxi
知，弓高h带来的不确定度分量为：
udD=∂D∂dud=-ud
从上式中可知,支承轮直径d的误差直接反映到测量结果误差上,因而在大直径测量仪中对支承轮直径的要求很高,支承轮与工件接触时,应具有较小的压力,从而避免支承轮因压力变形而造成的尺寸变化产生误差。另外支承轮应具有良好的耐磨性,避免因磨损而造成尺寸变化从而带来更大的误差。
3.2.4 合成标准不确定度
由公式ucy=i=1nui2y
得合成标准不确定度为：
ucD=uL2D+uh2D+ud2D
=L2huL2+(1-L24h2uh)2+ud2
为了更方便分析，由数学模型进行推导。
D=L24h+h-d
4hD=L2+4h2-4hd
4hD+4hd-4h2=L2
4hD+4hd-4h2h2=L2h2
4D+dh-4=L2h2
4D+dh-1=Lh2
假设c=D+dh
为灵敏系数，则Lh=2c-1
，所以∂D∂L=L2h=c-1
, ∂D∂h=1-L24h2=2-c
,则合成标准不确定度为：
ucD=uL2D+uh2D+ud2D
=c-1uL2+2-c2uh2+ud2
其中，uL2
--弦长的测量不确定度
uh2
--弓高的测量不确定度
ud2
--支承轮直径的测量不确定度
一般情况下,在测量设备、测量人员、测量环境都相同时,可近似地认为uLD=uhD=udD=K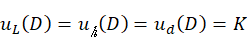
,则式一可化简为:
ucD=c-1+2-c2+1K
=c2-3c+4K
其中Q=c2-3c+4
称为弓高弦长测量法的综合灵敏系数。当c=1时, ucD=1.414K
，测量弓高就是测量直径,即直径的直接测量法。当c=2时, ucD=1.414K
，测量弦长也就是测量直径,即直径的直接测量法. 当1<c<2,在c=1.5式，测量不确定度ucD=1.323K
，为极小值。说明当h=1.5D时,测量不确定度最佳,说明此时用“弓高弦长”法测量比用直径的直接测量法更可靠。如图3.2所示。
图3.2 综合灵敏系数与c的关系
由图3.2中综合灵敏系数曲线可知当c≤10
,1.323K≤ucD≤8.61K
时，使用弓高弦长法测量较准确。根据c=D+dh
，h越大c越小,测量不确定度越稳定,该测量方法也越可靠。
当c≥20
,ucD≥15.55K
,由于误差急剧增大,测量不确定度随之不稳定且迅速变坏,使用“弓高弦长”法测量会使测量精度达不到工程测量的要求,故此时不宜采用“弓高弦长”法测量工件的直径。
第四章 不确定度计算
4.1 支承轮直径d与弦长L的标准不确定度
在对测量仪标定前, 首先用测长机测出测量仪两端测量头的直径d和测量头中心距L的值。JJF 1066 —2000《测长机校准规范》规定, 测长机示值误差为δ=±(0.5 +L/100) μm( L 为测量长度) 。测量仪测量头直径理论值为30mm, 则其误差为±0.80μm; 测量仪中心距理论值为435.89mm, 则其误差为 4.85μm。按均匀分布估计, 测长机示值误差引起的标准不确定度为:
ud=0.803=0.46 μm
uL=4.853=2.80 μm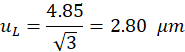
4.2 模拟弓高h的标准不确定度
模拟弓高 h的变化是通过量块实现的。在模拟不同直径时, 量块的组合方式不同, 引起的不确定度也不同。另外, 千分表也是影响模拟弓高 h 不确定度的因素之一。
4.2.1 量块引入的不确定度分量
根据量块的使用规程, 当量块组合使用时, 设单个 量块的长度为 L1, L2, …, Ln, 其长度测量不确定度为 u1, u2, … , un, 其研合后的长度测量不确定度为:
u1=u12+u22+u32+…+un2+(n-1)δ
其中：δ
--由于研合厚度发散而带来的不确定度, 一般为 0.02μm;
n--组合量块的块数。
采用二级量块, 查表可知, 不同组合量块引入的不确定度不同: 长度60 mm量块的测量不确定度为0.09μ m, 长度50mm、30 mm量块的测量不确定度为0.08μm, 长度20 mm 量块的测量不确定度为 0.07μm, 长度 ≤10 mm 量块的测量不确定度为 0.06 μm。
模拟直径为1000mm，模拟弓高为50mm，中间量块组合50 mm，uh=
0.08μm。
4.2.1 千分表引入的不确定度分量
千分表分辨力引入的标准不确定度u2。数字仪器不确定度的来源之一是其指示装置的分辨力。千分表的分辨力δx=1μm, 则
u2=0.29δx=0.29μm
测力变化引入的标准不确定度u3。千分表对测长机的接触为球面对平面接触, 根据经验值, 有u3
=0.05μm。
所以千分表引入的不确定度分量为u22+u32
。
各因素引起的模拟弓高h的合成标准不确定度为：
uh=u12+u22+u32=0.30μm
4.3 温度的标准不确定度
整个标定过程在环境温度为 25 ℃的条件下进行, 温度变化引起的不确定度可忽略。
4.4 合成标准不确定度
ucD =uL2D+uh2D+ud2D
=L2huL2+(1-L24h2uh)2+ud2
=
13.35 μm
4.5 拓展不确定度
置信概率99%, k取3。
U=k×uc=3×13.35μm=40.05μm
2614
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
