目录
HJ151 模意义下最大子序列和(Easy Version)
入门难度
HJ7 取近似值
描述:
对于给定的正实数x,输出其四舍五入后的整数。更具体地说,若x的小数部分大于等于0.5,则输出向上取整后的整数;否则输出向下取整后的整数。
输入描述:
输入一个小数点后位数不超过5位的实数x(0<x≦20)。保证实数不存在前导零和后导零。
输出描述:
在一行上输出一个整数,代表x四舍五入后的结果。
解题思路:
BigDecimal.setScale(int newScale, int roundingMode),格式化小数点,小数点为0,近似方法为四舍五入BigDecimal.ROUND_HALF_UP
import java.math.*;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String string = in.nextLine();
BigDecimal bigDecimal = new BigDecimal(string);
System.out.println(bigDecimal.setScale(0, BigDecimal.ROUND_HALF_UP));
}
}HJ9 提取不重复的整数
描述:
对于给定的正整数n,按照从右向左的阅读顺序,返回一个不含重复数字的新的整数。具体地,如果遇到相同数字,保留在最右侧出现的第一个数字。
输入描述:
在一行上输入一个整数n(1≦n≦10⁸)代表给定的整数。保证n的最后一位不为0。
输出描述:
在一行上输出一个整数,代表处理后的数字。
解题思路:
StringBuffer.reverse(),翻转字符串,String.toCharArray(),字符串转字符数组,再用LinkedHashSet依次获取出现的字符,LinkedHashSet保证Set内元素按输入次序排序
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
StringBuffer stringBuffer = new StringBuffer(in.nextLine()).reverse();
char[] chars = stringBuffer.toString().toCharArray();
Set<Character> set = new LinkedHashSet<>();
for (char c : chars) {
set.add(c);
}
for (Character c : set) {
System.out.print(c);
}
}
}HJ42 构造C的歪
描述:
小歪有两个整数a和b,他想找到这样一个整数c,使得这三个整数在经过排序后能成为一个等差数列。
输入描述:
在一行上输入两个整数a,b(1≦a,b≦10⁶)代表已有的数字。
输出描述:
在一行上输出一个整数代表你所找到的第三个数字。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。
解题思路:
a加上a减b的差,一定能和a,b组成等差数列
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int b = in.nextInt();
System.out.println(a + (a - b));
}
}HJ46 截取字符串
描述:
对于给定的字符串s和整数k,截取字符串s的前k个字符后输出。
输入描述:
第一行输入一个长度为1≦len(s)≦10³、由小写字母和大写字母混合构成的字符串s。
第二行输入一个整数k(1≦k≦len(s))代表截取字符串的长度。输出描述:
输出一个长度为k的字符串,表示截取字符串s的前k个字符。
解题思路:
String.substring(int beginIndex, int endIndex),beginIndex为0,endIndex为截取的长度
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String string = in.nextLine();
int k = in.nextInt();
System.out.println(string.substring(0, k));
}
}HJ47 【模板】排序
描述:
给定一个长度为n的整数数组A(允许元素重复),请将其按非递减顺序排序并输出。
输入描述:
第一行输入整数 n(1≦n≦10⁵),表示数组长度。
第二行输入n个整数a₁,a₂,…,aₙ(−10⁹≦aᵢ≦10⁹)。输出描述:
在一行上输出排序后的数组,各元素以空格分隔。
解题思路:
Arrays.sort(int[] a),对数组升序排序,然后输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] ints = new int[n];
for (int i = 0; i < n; i++) {
ints[i] = in.nextInt();
}
Arrays.sort(ints);
for (int i = 0; i < n; i++) {
System.out.print(ints[i]);
if (i != n - 1) {
System.out.print(" ");
}
}
}
}HJ58 输入n个整数,输出其中最小的k个
描述:
对于输入的n个整数,升序输出其中最小的k个。
输入描述:
第一行输入两个整数n,k(1≦n≦1000;1≦k≦n)。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁴)代表给定的数字。输出描述:
在一行中升序输出最小的k个整数。
解题思路:
Arrays.sort(int[] a),对数组升序排序,然后输出前k个
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
int[] ints = new int[n];
for (int i = 0; i < n; i++) {
ints[i] = in.nextInt();
}
Arrays.sort(ints);
for (int i = 0; i < k; i++) {
System.out.print(ints[i]);
if (i != k - 1) {
System.out.print(" ");
}
}
}
}HJ101 排序
描述:
对于给出的n个整数组成的数组{a₁,a₂,…,aₙ},根据输入要求,按升序或降序排列后输出。
输入描述:
第一行输入一个整数n(1≦n≦10³)代表数组中的元素个数。
第二行输入n个整数a₁,a₂,…,aₙ(0≦aᵢ≦10⁵)代表数组中的元素。
第三行输入一个整数op(0≦op≦1)代表排序方式,其中,op=0表示按升序,op=1表示按降序。输出描述:
在一行上输出n个整数,代表排序后的数组。
解题思路:
Arrays.sort(int[] a),对数组升序排序,然后根据参数op,正序或者倒叙遍历数组
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] ints = new int[n];
for (int i = 0; i < n; i++) {
ints[i] = in.nextInt();
}
int op = in.nextInt();
Arrays.sort(ints);
if (op == 0) {
for (int i = 0; i < n; i++) {
System.out.print(ints[i]);
if (i != n - 1) {
System.out.print(" ");
}
}
} else {
for (int i = n - 1; i >= 0; i--) {
System.out.print(ints[i]);
if (i != 0) {
System.out.print(" ");
}
}
}
}
}HJ107 构造A+B
描述:
对于给定的两个正整数n和k,是否能构造出k对不同的正整数(x,y),使得x+y=n。
我们认为两对正整数(x,y)和(x′,y′)是不同的,当且仅当x≠x′。
输入描述:
第一行输入两个整数n,k(1≦n,k≦10⁵),含义如题中所述。
输出描述:
如果存在满足题意的k对不同正整数,在一行上输出YES;否则,直接输出NO。
解题思路:
如果n-1≥k,则成立,因为从1开始和为n的正整数对,有n-1种
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
if (n - 1 >= k) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}HJ114 小红的正整数构造
描述:
给定一个闭区间[l,r]以及一个正整数x。
请在区间内找到一个整数y,满足y是x的倍数,即y≡0(mod x)。
若存在多个满足条件的y,输出任意一个;若不存在,输出−1。输入描述:
在一行上输入三个整数l,r,x(1≦l≦r≦10²; 1≦x≦10²)——区间左右端点与基准倍数。
输出描述:
若存在满足条件的整数y,在一行上输出y;否则输出−1。
如果存在多个答案,可以输出任意一个,系统会自动判断其正确性。
解题思路:
[l,r]区间循环对x取余,余数为0,然后输出返回,如果循环到最后仍然余数不为0,输出-1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int l = in.nextInt();
int r = in.nextInt();
int x = in.nextInt();
for (int i = l; i <= r; i++) {
if (i % x == 0) {
System.out.println(i);
return;
}
}
System.out.println(-1);
}
}HJ120 彩虹糖的梦
描述:
有红橙黄绿青蓝紫七种不同颜色的彩虹糖,第i种颜色的彩虹糖有aᵢ个。
每一位小朋友都想要吃到全部七种颜色的彩虹糖。最多可以分给多少个小朋友?输入描述:
第一行输入七个整数a₁,a₂,…,a₇(1≤aᵢ≤10⁹)代表七种颜色的彩虹糖数量。
输出描述:
在一行上输出一个整数,代表最多可以分给多少个小朋友。
解题思路:
本质就是获取数组中最小值,Arrays.sort(int[] a),对数组升序排序,然后输出a[0]
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int[] ints = new int[7];
for (int i = 0; i < 7; i++) {
ints[i] = in.nextInt();
}
Arrays.sort(ints);
System.out.println(ints[0]);
}
}HJ126 小红的正整数计数
描述:
小红拿到了一个区间[l,r](这代表从数字l开始,l+1,l+2,⋯一直到r这r−l+1个数字),她想知道该区间内有多少个数是2的倍数。你能帮帮她吗?
输入描述:
在一行上输入两个整数l,r(1≦l≦r≦100)代表区间的左右边界。
输出描述:
输出一个整数,表示区间内2的倍数的个数。
解题思路:
[l,r]区间循环对2取余,余数为0时,增加计数,然后输出计数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int l = in.nextInt();
int r = in.nextInt();
int result = 0;
for (int i = l; i <= r; i++) {
if (i % 2 == 0) {
result++;
}
}
System.out.println(result);
}
}HJ140 小红的合数寻找
描述:
小红拿到了一个正整数x,她希望你在[x,2×x]区间内找到一个合数,你能帮帮她吗?
一个数为合数,当且仅当这个数是大于1的整数,并且不是质数。输入描述:
在一行上输入一个正整数x(1≦x≦100)。
输出描述:
如果范围内不存在符合条件的合数,则输出−1。否则,输出一个正整数代表答案。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确
解题思路:
输入是1返回-1,因为1和2都不是合数,否则返回原数2倍,一定是合数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int x = in.nextInt();
if (x == 1) {
System.out.println(-1);
} else {
System.out.println(2 * x);
}
}
}HJ146 谐距下标对
描述:
给定一个长度为n的整数数组{a₁,a₂,…,aₙ}。若下标满足i<j且aⱼ−aᵢ=j−i,则称(i,j) 为一对谐距下标对。
请计算数组中的谐距下标对数量。输入描述:
第一行输入整数n(1≦n≦10⁵)。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁵)。输出描述:
输出一个整数,表示谐距下标对数量。
解题思路:
计算数组第i个元素,和i之间的差,如果差相同,则差出现次数记录加1,存入Map,Map.getOrDefault(Object key, V defaultValue),为Map中元素不存在时的默认值,遍历Map,累加差出现次数大于等于2次的n*(n - 1)/2,即Cn2
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
Map<Integer, Integer> counts = new HashMap<>();
int n = in.nextInt();
for (int i = 0; i < n; i++) {
int a = in.nextInt();
int diff = a - i;
counts.put(diff, counts.getOrDefault(diff, 0) + 1);
}
long totalParis = 0;
for (int count : counts.values()) {
if (count > 1) {
totalParis += (long) count * (count - 1) / 2;
}
}
System.out.println(totalParis);
}
}HJ165 小红的优惠券
描述:
小红的购物车结算金额为n元,她手中有m张优惠券。第j张优惠券的规则为“满aⱼ元立减bⱼ元”,即若n≧aⱼ,则使用该券后需支付n−bⱼ元。
小红至多使用一张优惠券,请问最少需要支付多少元?输入描述:
第一行输入两个整数n,m(1≦n≦10⁵; 1≦m≦100)。
接下来m行,第j行输入两个整数aⱼ,bⱼ(1≦bⱼ≦aⱼ≦10⁵),描述第j张优惠券。输出描述:
输出一个整数,表示小红使用最优策略后需支付的最少金额。
解题思路:
循环读取,检查是否满足优惠券条件,满足计算折扣后金额,Math.min(int a, int b),获取最小值,即最小折扣后金额
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int result = n;
for (int i = 0; i < m; i++) {
int i1 = in.nextInt();
int i2 = in.nextInt();
if (n >= i1) {
result = Math.min(result, n - i2);
}
}
System.out.print(result);
}
}HJ166 讨厌鬼进货
描述:
讨厌鬼需要采购n种货物,每种货物可通过以下方式获取:
- 在供应商A以aᵢ元购得第i种;
- 在供应商B以bᵢ元购得第i种;
- 在网购平台一次性购买全部n种,花费x元(不能拆分)。
可以自由组合以上方式,只要最终每种货物都至少购买一件。求最小总花费。
输入描述:
第一行输入两个整数n,x(1≦n≦10⁵; 1≦x≦10⁹)。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁴)。
第三行输入n个整数b₁,b₂,…,bₙ(1≦bᵢ≦10⁴)。输出描述:
输出一个整数,表示完成采购的最少花费。
解题思路:
获取从A和B进货的每一件产品的最小值,Math.min(int a, int b),获取最小值,对每一件产品的最小值相加,比较网购总价,获取最小总价
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int x = in.nextInt();
int[] aInts = new int[n];
int[] bInts = new int[n];
int total = 0;
for (int i = 0; i < n; i++) {
aInts[i] = in.nextInt();
}
for (int i = 0; i < n; i++) {
bInts[i] = in.nextInt();
}
for (int i = 0; i < n; i++) {
total += Math.min(aInts[i], bInts[i]);
}
System.out.println(Math.min(total, x));
}
}简单难度
HJ1 字符串最后一个单词的长度
描述:
对于给定的若干个单词组成的句子,每个单词均由大小写字母混合构成,单词间使用单个空格分隔。输出最后一个单词的长度。
输入描述:
在一行上输入若干个字符串,每个字符串代表一个单词,组成给定的句子。
除此之外,保证每个单词非空,由大小写字母混合构成,且总字符长度不超过10³ 。输出描述:
在一行上输出一个整数,代表最后一个单词的长度。
解题思路:
String.split(String regex),按" "切分字符串获取String数组,取最后一个数组元素的长度
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] words = in.nextLine().split(" ");
String lastWord = words[words.length - 1];
System.out.println(lastWord.length());
}
}HJ2 计算某字符出现次数
描述:
对于给定的由大小写字母、数字和空格混合构成的字符串s,给定字符c,按要求统计:
- 若c为大写或者小写字母,统计其大小写形态出现的次数和;
- 若c为数字,统计其出现的次数。
保证字符c要么为字母、要么为数字。
输入描述:
第一行输入一个长度 1≦length(s)≦10³,由大小写字母、数字和空格构成的字符串s。保证首尾不为空格。
第二行输入一个字符c,保证c为大小写字母或数字。输出描述:
在一行上输出一个整数,代表统计结果。
解题思路:
String.toLowerCase(),字符串和需要匹配的字符,同时转成小写,再转为字符数组,再依次比较,算出匹配的字符出现的次数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.nextLine().toLowerCase().trim().toCharArray();
char matchChar = in.nextLine().toLowerCase().trim().charAt(0);
int result = 0;
for (char c : chars) {
if (matchChar == c) {
result++;
}
}
System.out.println(result);
}
}HJ4 字符串分隔
描述:
对于给定的由小写字母和数字混合构成的字符串s,你需要按每8个字符换一行的方式书写它,具体地:
- 书写前8个字符,换行;
- 书写接下来的8个字符,换行;
- 重复上述过程,直到字符串被完全书写。
特别地,如果最后一行不满8个字符,则需要在字符串末尾补充0,直到长度为8。
输入描述:
在一行上输入一个长度 1≦length(s)≦100,由小写字母和数字构成的字符串s。
输出描述:
输出若干行,每行输出8个字符,代表按题意书写的结果。
解题思路:
用字符串长度取余,补上8-余数%8,然后每8个字符打印
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String string = in.nextLine();
if (string.length() % 8 != 0) {
int add = 8 - string.length() % 8;
for (int i = 0; i < add; i++) {
string += "0";
}
}
for (int i = 0; i < string.length(); i += 8) {
System.out.println(string.substring(i, i + 8));
}
}
}HJ5 进制转换
描述:
对于给定的十六进制数,输出其对应的十进制表示。
在本题中,十六进制数的格式为:0x开头,后跟若干个十六进制数字(保证为0-9和A-F中的一个)。其中,A-F依次代表十进制中的10∼15。输入描述:
在一行上输入一个十六进制数s,代表待转换的十六进制数,格式见题干。保证s转化得到的十进制数x的范围为1≦x<2³¹。
输出描述:
在一行上输出一个整数,代表s对应的十进制数。
解题思路:
String.replace(CharSequence target, CharSequence replacement),把字符串的0x或者0X子串去掉,Long.parseLong(String s, int radix),使用Long类自带的16进制转10进制方法
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String hexString = in.nextLine().replace("0x","").replace("0X","");;
long result = Long.parseLong(hexString, 16);
System.out.println(result);
}
}HJ6 质数因子
描述:
对于给定的整数n从小到大依次输出它的全部质因子。即找到这样的质数p₁,p₂,⋯ ,pₖ,使得n=p₁×p₂×⋯×pₖ。
输入描述:
在一行上输入一个整数n(2≦n≦2×10⁹+14)代表待分解的整数。
输出描述:
在一行上从小到大输出若干个整数,代表n的质因子。
解题思路:
从2开始,将输入参数取余,取余为0代表这个数是质因子,将这个数加入结果集合,然后将入参除以这个质因子,然后重新从2开始算,一直取到入参的开方数,如果这个过程最后的除以数字不为1,就将最后的余数加入结果集合,然后遍历打印
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int inputInt = in.nextInt();
int maxSplit = (int) Math.sqrt(inputInt);
List<Integer> intList = new ArrayList<>();
for (int i = 2; i <= maxSplit; ) {
if (inputInt % i == 0) {
inputInt = inputInt / i;
intList.add(i);
i = 2;
} else {
i++;
}
}
if (inputInt != 1) {
intList.add(inputInt);
}
for (int i = 0; i < intList.size(); i++) {
System.out.print(intList.get(i));
if (i != intList.size() - 1) {
System.out.print(" ");
}
}
}
}HJ8 合并表记录
描述:
数据表中,一条记录包含表索引和数值两个值。请对表索引相同的记录进行合并(即将相同索引的数值进行求和运算),随后按照索引值的大小从小到大依次输出。
输入描述:
第一行输入一个整数n(1≦n≦500)代表数据表的记录数。
此后n行,第i行输入两个整数xᵢ,yᵢ(0≦xᵢ≦11111111;1≦yᵢ≦10⁵)代表数据表的第i条记录的索引和数值。输出描述:
一共若干行(视输入数据变化),第i行输出两个整数,代表合并后数据表中第i条记录的索引和数值。
解题思路:
使用TreeMap,TreeMap按照key排序,依次遍历打印
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
Map<Integer, Integer> map = new TreeMap<>();
for (int i = 0; i < n; i++) {
int a = in.nextInt();
int b = in.nextInt();
map.put(a, map.getOrDefault(a, 0) + b);
}
for (int key : map.keySet()) {
System.out.println(key + " " + map.get(key));
}
}
}HJ10 字符个数统计
描述:
对于给定的字符串,统计其中的ASCII码在0到127范围内的不同字符的个数。
输入描述:
输入一个长度 1≦length(s)≦500,仅由图片中的可见字符构成的字符串s。
输出描述:
在一行上输出一个整数,代表给定字符串中ASCII码在0到127范围内的不同字符的个数。
解题思路:
字符串转字符数组,遍历字符数组,使用Set集合去重,获取Set大小
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] input = in.nextLine().toCharArray();
Set<Character> set = new HashSet<>();
for (int i = 0; i < input.length; i++) {
set.add(input[i]);
}
System.out.println(set.size());
}
}HJ11 数字颠倒
描述:
对于给定的非负整数n,将其以字符串的形式颠倒后输出。这意味着,如果n的末尾含0,那么返回的字符串开头也需要含0。
输入描述:
在一行上输入一个非负整数 n(0≦n<2³⁰)代表给定的整数。
输出描述:
在一行上输出一个字符串,代表颠倒后的数字。
解题思路:
使用StringBuilder类reverse方法颠倒
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
StringBuilder stringBuilder = new StringBuilder(s);
System.out.println(stringBuilder.reverse());
}
}HJ12 字符串反转
描述:
对于给定的仅由小写字母构成的字符串s,将其倒过来输出。
输入描述:
在一行上输入一个长度 1≦length(s)≦10³,仅由小写字母构成的字符串s。
输出描述:
在一行上输出一个字符串,代表颠倒后的字符串。
解题思路:
使用StringBuilder类reverse方法颠倒
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
StringBuilder stringBuilder = new StringBuilder(s);
System.out.println(stringBuilder.reverse());
}
}HJ13 句子逆序
描述:
对于给定的若干个单词组成的句子,每个单词均由大小写字母混合构成,单词间使用单个空格分隔。输出以单词为单位逆序排放的结果,即仅逆序单词间的相对顺序,不改变单词内部的字母顺序。
输入描述:
在一行上输入若干个字符串,每个字符串代表一个单词,组成给定的句子。
除此之外,保证每个单词非空,由大小写字母混合构成,且总字符长度不超过10³。输出描述:
在一行上输出一个句子,代表以单词为单位逆序排放的结果。
解题思路:
使用split拆分为String数组,逆向拼接打出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] s = in.nextLine().split(" ");
for (int i = s.length - 1; i >= 0; i--) {
System.out.print(s[i]);
if (i != 0) {
System.out.print(" ");
}
}
}
}HJ14 字符串排序
描述:
对于给定的由大小写字母混合构成的n个单词,输出按字典序从小到大排序后的结果。
输入描述:
第一行输入一个整数n(1≦n≦10³)代表给定的单词个数。
此后n行,每行输入一个长度1≦length(s)≦100,由大小写字母构成的字符串s,代表一个单词。输出描述:
一共n行,每行输出一个字符串,代表排序后的结果。第一行输出字典序最小的单词。
解题思路:
使用List类接收,sort方法排序,然后输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
List<String> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
list.add(in.next());
}
list.sort(null);
for (int i = 0; i < n; i++) {
System.out.println(list.get(i));
}
}
}HJ15 求int型正整数在内存中存储时1的个数
描述:
对于给定的int型的十进制整数n,统计其在内存中存储时1的个数。换句话说,即统计其二进制表示中1的个数。
输入描述:
在一行上输入一个整数n(0≦n<2³¹),代表给定的数字。
输出描述:
在一行上输出一个整数,代表n的二进制表示中1的个数。
解题思路:
使用Integer类toBinaryString方法转为二进制字符串,然后转为字符数组,然后匹配'1'字符
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] binCharArray= Integer.toBinaryString(in.nextInt()).toCharArray();
int result = 0;
for (int i = 0 ; i < binCharArray.length ; i ++) {
if ('1' == binCharArray[i]) {
result++;
}
}
System.out.println(result);
}
}HJ21 简单密码
描述:
规定这样一种密码的变换方法:
- 对于密码中的小写字母,参考九键手机键盘,将它们映射为对应的数字,具体地,abc对应数字2、def对应数字3 、ghi对应数字4 、jkl对应数字5 、mno对应数字6 、pqrs对应数字7、tuv对应数字8、wxyz对应数字9;
- 对于密码中的大写字母,先将其转换为小写,然后向后移动一位,即Z转换为a,A转换为b,B转换为c,⋯⋯ ,Y转换为z,Z转换为a。
- 对于密码中的数字,保持不变。
现在,请你将给定的密码按照上述规则进行变换。
输入描述:
在一行上输入一个长度为1≦length(s)≦100的字符串s,代表给定的密码。
输出描述:
在一行上输出一个字符串,代表变换后的密码。
解题思路:
按照ASCII码和Character方法转换
import java.util.Scanner;
public class Main {
// 按照ASCII码转换
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] inputArray = in.next().toCharArray();
StringBuffer result = new StringBuffer();
for (int i = 0; i < inputArray.length; i++) {
// abc对应数字2
if (inputArray[i] >= 97 && inputArray[i] <= 99) {
result.append(2);
// def对应数字3
} else if (inputArray[i] >= 100 && inputArray[i] <= 102) {
result.append(3);
// ghi对应数字4
} else if (inputArray[i] >= 103 && inputArray[i] <= 105) {
result.append(4);
// jkl对应数字5
} else if (inputArray[i] >= 106 && inputArray[i] <= 108) {
result.append(5);
// mno对应数字6
} else if (inputArray[i] >= 109 && inputArray[i] <= 111) {
result.append(6);
// pqrs对应数字7
} else if (inputArray[i] >= 112 && inputArray[i] <= 115) {
result.append(7);
// tuv对应数字8
} else if (inputArray[i] >= 116 && inputArray[i] <= 118) {
result.append(8);
// wxyz对应数字9
} else if (inputArray[i] >= 119 && inputArray[i] <= 122) {
result.append(9);
// 大写字母,先将其转换为小写,然后向后移动一位,Z转为a
} else if (Character.isUpperCase(inputArray[i])) {
if (inputArray[i] == 'Z') {
result.append("a");
} else {
char temp = Character.toLowerCase(inputArray[i]);
char[] s = Character.toChars(temp + 1);
result.append(s);
}
} else {
result.append(inputArray[i]);
}
}
System.out.println(result);
}
}HJ22 汽水瓶
描述:
某商店规定:三个空汽水瓶可以换一瓶汽水,允许向老板借空汽水瓶(但是必须要归还)。
小张手上有n个空汽水瓶,她想知道自己最多可以喝到多少瓶汽水。输入描述:
本题将会给出1≦T≦10组测试数据,确切数字未知,您需要一直读入直到特定的结尾;每组测试数据描述如下:
在一行上输入一个整数n(0≦n≦100),代表小张手上的空汽水瓶数量。特别地,n=0代表输入结束,您只需要立即退出,不需要针对这种情况进行处理。输出描述:
对于每一组测试数据,新起一行。输出
解题思路:
小于3个是0,大于等于3个是数量/2
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (true) {
int input = in.nextInt();
if (input == 0) {
return;
}
if (input < 3) {
System.out.println(0);
} else {
System.out.println(input / 2);
}
}
}
}HJ23 删除字符串中出现次数最少的字符
描述:
对于给定的仅由小写字母构成的字符串,删除字符串中出现次数最少的字符。输出删除后的字符串,字符串中其它字符保持原来的顺序。
特别地,若有多个字符出现的次数都最少,则把这些字符都删除。输入描述:
在一行上输入一个长度为1≦length(s)≦20,仅由小写字母构成的字符串s,代表待处理的字符串。
输出描述:
在一行上输出一个字符串,代表删除后的答案。保证这个字符串至少包含一个字符。
解题思路:
字符串转字符数组,然后对字符用Map进行计数,然后遍历,获取出现最少的字符的数量,然后将原始字符串中出现最少的字符替换掉
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String input = in.next();
char[] array = input.toCharArray();
Map<Character, Integer> map = new HashMap<>();
for (int i = 0; i < array.length; i++) {
map.put(array[i], map.getOrDefault(array[i], 0) + 1);
}
int min = Integer.MAX_VALUE;
for (char key : map.keySet()) {
if (map.get(key) < min) {
min = map.get(key);
}
}
for (char key : map.keySet()) {
if (map.get(key) == min) {
input = input.replaceAll(key + "", "");
}
}
System.out.println(input);
}
}HJ31 单词倒排
描述:
对于给定的若干个单词组成的句子,每个单词均由大小写字母构成,单词间使用非字母字符分隔。输出以单词为单位逆序排放的结果,即仅逆序单词间的相对顺序,不改变单词内部的字母顺序。
特别地,在输出结果中,去除原有的分隔符,转而使用单个空格间隔单词。输入描述:
在一行上输入若干个字符串,每个字符串长度为1≦length(s)≦20,仅由大小写字母构成,代表一个单词。单词间还夹杂了一定数量的非字母字符(但保证是可见字符),代表分隔符。
除此之外,保证总字符长度不超过10⁴。输出描述:
在一行上输出一个句子,代表以单词为单位逆序排放的结果。单词间使用单个空格分隔。
解题思路:
字符串转字符数组,遍历数组,拼接字符,碰到特殊字符,将之前拼接好的字符串放入list,list倒序输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] inputCharArray = in.nextLine().toCharArray();
String tempString = "";
List<String> list = new ArrayList<>();
for (int i = 0; i < inputCharArray.length; i++) {
if (Character.isAlphabetic(inputCharArray[i])) {
tempString += inputCharArray[i];
} else {
if (tempString != "") {
list.add(tempString);
tempString = "";
}
}
if (i == inputCharArray.length - 1) {
if (tempString != "") {
list.add(tempString);
tempString = "";
}
}
}
Collections.reverse(list);
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i));
if (i != list.size() - 1) {
System.out.print(" ");
}
}
}
}HJ34 图片整理
描述:
对于给定的由大小写字母和数字组成的字符串,请按照ASCII码值将其从小到大排序。
输入描述:
在一行上输入一个长度为1≦length(s)≦10³,仅由大小写字母和数字构成的字符串s,代表输入的字符串。
输出描述:
在一行上输出一个字符串s,代表排序后的答案。
解题思路:
字符串转字符数组,字符数组根据ASCII码排序,字符数组默认就是按ASCII码排序,然后输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] inputCharArray = in.next().toCharArray();
Arrays.sort(inputCharArray);
String str = new String(inputCharArray);
System.out.println(str);
}
}HJ35 蛇形矩阵
描述:
你需要输出一个n行n列的上三角形蛇形矩阵。
具体的构造方法为,从1开始填充自然数,记第i行第1列的元素为=k,将其右上角的元素
依次赋值为k+1,k+2,⋯ ,k+i−1,随后,将
赋值为k+i,并重复上述过程,直到填满上三角范围n*(n+1)/2个格子。
输入描述:
在一行上输入一个整数n(1≦n≦100)代表矩阵的大小。
输出描述:
输出一个n行n列的上三角蛇形矩阵。
解题思路:
矩阵第i行,排i个元素,按1,2,3……顺序依次排,然后把每一列,都按顺序移动到最前面,这样就是蛇形矩阵,然后打印
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[][] array = new int[n][n];
int temp = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
temp++;
array[i][j] = temp;
}
}
for (int j = 0; j < n; j++) {
for (int i = 0; i < n; i++) {
if (array[i][j] != 0) {
temp = array[i][j];
array[i][j] = 0;
array[i - j][j] = temp;
}
}
}
for (int i = 0; i < n; i++) {
String s = "";
for (int j = 0; j < n; j++) {
if (array[i][j] != 0) {
s += array[i][j];
s += " ";
}
}
System.out.println(s.trim());
}
}
}HJ37 统计每个月兔子的总数
描述:
有一种兔子,从出生后第三个月起,每个月都会生一只兔子,生出来的兔子同理。假设兔子都不死,求解第n个月时的兔子总数。
输入描述:
在一行上输入一个整数n(1≦n≦31)代表查询的月份。
输出描述:
在一行上输出一个整数,代表第n个月的兔子总数。
解题思路:
典型的斐波那契数列
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
System.out.println(calc(a));
}
public static int calc(int a) {
if (a == 1 || a == 2) {
return 1;
} else {
return calc(a - 1) + calc(a - 2);
}
}
}HJ40 统计字符
描述:
对于给定的由可见字符和空格组成的字符串,统计其中英文字母、空格、数字和其它字符的个数。
字符串由 ASCII 码在32到126范围内的字符组成。您可以参阅下表获得其详细信息。输入描述:
在一行上输入一个长度为1≦length(s)≦1000的字符串。
输出描述:
第一行输出一个整数,代表字符串中英文字母的个数。
第二行输出一个整数,代表字符串中空格的个数。
第三行输出一个整数,代表字符串中数字的个数。
第四行输出一个整数,代表字符串中其它字符的个数。
解题思路:
字符串转字符数组,遍历数组,按照Character类isAlphabetic,isDigit方法统计,然后输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] array = in.nextLine().toCharArray();
int[] result = new int[4];
for (char c : array) {
if (Character.isAlphabetic(c)) {
result[0]++;
} else if (c == ' ') {
result[1]++;
} else if (Character.isDigit(c)) {
result[2]++;
} else {
result[3]++;
}
}
for (int i = 0; i < result.length; i++) {
System.out.println(result[i]);
}
}
}HJ49 分数线划定
描述:
某市为世博会选拔志愿者,先进行笔试,再按笔试成绩划定面试分数线。规则如下:
- 计划最终录取m名志愿者;
- 面试名额定为m的150%,向下取整,记为t=⌊1.5m⌋;
- 将所有报名号及笔试成绩按成绩从高到低、成绩相同报名号从小到大排序;
第t名选手的成绩即为面试分数线;
- 所有笔试成绩不低于该分数线的选手均进入面试。
请输出面试分数线及所有进入面试选手的信息(按排序后的顺序)。
输入描述:
第一行输入两个整数n,m(5≦n≦5000; 3≦m≦n),分别表示报名人数与计划录取人数。
接下来n行,每行输入两个整数k,s(1000≦k≦9999; 1≦s≦100),分别为报名号与笔试成绩。报名号保证唯一。输出描述:
第一行输出两个整数:面试分数线line与进入面试的人数cnt。
接下来cnt行,按排序顺序输出每位选手的报名号k与成绩s,每行两个整数,用空格分隔。
解题思路:
设置Person实体类,计算面试入围人员,按照分数和编号依次排名,获取list中排名为面试入围人数-1的人的分数做为入围分数线,分数大于等于入围分数线的再加入一个新list,获取分数和人数和名单
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int countLine = (int) (m * 1.5);
List<Person> personList = new ArrayList<>();
for (int i = 0; i < n; i++) {
int order = in.nextInt();
int scole = in.nextInt();
personList.add(new Person(order, scole));
}
personList.sort((a1, b1) -> {
if (a1.scole != b1.scole) {
return b1.scole - a1.scole;
} else {
return a1.order - b1.order;
}
});
Person line = personList.get(countLine - 1);
List<Person> person2List = new ArrayList<>();
for (Person p : personList) {
if (p.scole >= line.scole) {
person2List.add(p);
} else {
break;
}
}
System.out.println(line.scole + " " + person2List.size());
for (Person p : person2List) {
System.out.println(p.order + " " + p.scole);
}
}
public static class Person {
public int order;
public int scole;
public Person(int order, int scole) {
this.order = order;
this.scole = scole;
}
}
}HJ51 输出单向链表中倒数第k个结点
描述:
输入一个单向链表,输出该链表中倒数第k个结点,链表的倒数第1个结点为链表的尾指针。
链表结点定义如下:
struct ListNode { int val; ListNode* m_pNext; };正常返回倒数第k个结点指针。
输入描述:
每一个测试用例会有多组。每一组的测试用例格式如下:
第一行输入链表结点个数n,1≤n≤1000
第二行输入长度为n的数组val,表示链表的每一项,0≤val[i]≤10000
第三行输入k的值,k≤n
输出描述:
每一组,输出倒数第k个结点的值
解题思路:
存入数组,然后根据k拿到数组中的元素
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int n = in.nextInt();
int[] val = new int[n];
for (int i = 0; i < n; i++) {
val[i] = in.nextInt();
}
int k = in.nextInt();
System.out.println(val[n - k]);
}
}
}HJ53 杨辉三角的变形
描述:
定义变形的杨辉三角规则:
- 第一行为固定的整数1;
- 第二行开始,每行的数字数量均比上一行多两个,且中心对称(也可以看作是在上一行的基础上首尾增加了一个数字);每个位置上的数字是它正上方、左上角和右上角这三个数之和(如果不存在某个数,认为该数就是0)。
下方展示了计算的过程:
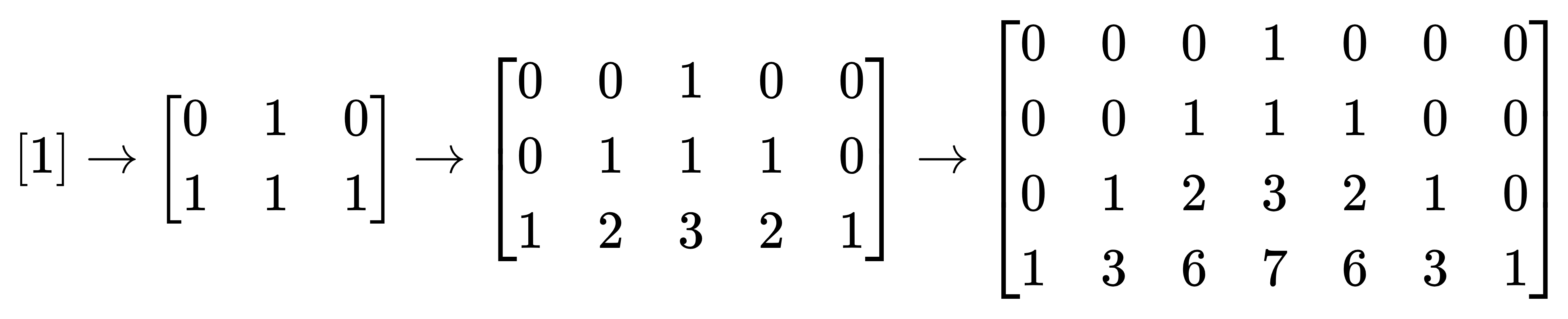
现在,你需要输出第n行中第一个偶数出现的位置。从1开始计数。
输入描述:
输入一个整数n(1≦n≦10⁹)代表询问的行数。
输出描述:
输出一个整数,代表第n行中第一个偶数出现的位置。特别地如果第n行中没有偶数,则输出−1。
解题思路:
找规律,只有1行或者2行,就是没有,如果是奇数行,就是2,如果是非4的倍数就是4,否则就是3
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
if (n == 1 || n == 2) {
System.out.println("-1");
return;
}
if (n % 2 != 0) {
System.out.println("2");
return;
}
if (n % 4 != 0) {
System.out.println("4");
} else {
System.out.println("3");
}
}
}HJ54 不要三句号的歪
描述:
在书写超过3个的连续的数字时,我们通常会将第一、二项和最后一项写出,中间的部分使用三个英文句号作为省略号 ...... 替代,例如,2,3,...,7其实就是使用省略号省略了4,5,6这三个数字。
现在,对于给定的数列,你需要直接求解出省略了多少数字。输入描述:
在一行上输入一个长度不超过20的字符串。具体的规范为:仅包含三个无符号十进制整数a,b,c(0≤a,b,c≤10¹²; a+1=b; b+1<c),形如a,b,...,c;数字a与b间使用一个半角逗号间隔;省略号部分由三个连续半角句号构成,且前后各有一个半角逗号。
输出描述:
在一行上输出一个整数代表被省略的数字数量。
解题思路:
字符串用","分割,然后数组最后一个元素的值,减去数组第一个元素的值,再减去2,就是省略的数字数量
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] strings = in.nextLine().split(",");
System.out.println(Long.valueOf(strings[strings.length - 1]) - Long.valueOf(strings[0]) - 2);
}
}HJ56 完全数计算
描述:
完全数,又称完美数或完备数,是一些特殊的自然数。它所有的真因子(即除了自身以外的约数)之和恰好等于它本身。
现在,你需要计算1到n之间完全数的个数。输入描述:
输入一个整数 n(1≦n≦5×10⁵)。
输出描述:
输出一个整数,代表区间内完全数的个数。
解题思路:
先从1开始取余,如果取余为0,代表是约数,并且不重新从1开始算,因为完全数的约数不能重复,然后将去除本身后约数相加,判断等不等于原本的数,for循环判断区间,计算完全数数量
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int input = in.nextInt();
int result = 0;
for (int i = 1; i <= input; i++) {
if (isPerfectNumber(i)) {
result++;
}
}
System.out.println(result);
}
public static boolean isPerfectNumber(int number) {
// 最小的完全数是6(1, 2, 3的和)
if (number < 6) {
return false;
}
int sum = 0;
// 只检查到number的一半即可,因为因子不会大于number的一半
for (int i = 1; i <= number / 2; i++) {
// 如果i是number的因子,累加因子
if (number % i == 0) {
sum += i;
}
}
// 如果因子的和等于原数,则是完全数
return sum == number;
}
}HJ60 查找组成一个偶数最接近的两个素数
描述:
对于给定的偶数n,找出两个素数a,b,满足:
- 它们的和等于n;
- 它们的差值的绝对值最小。
我们可以证明,a,b一定存在,从小到大输出满足条件的素数对。
输入描述:
输入一个整数n(4≦n≦10³)。保证n是偶数。
输出描述:
第一行输出一个整数a,代表满足条件的素数对中的较小者。
第二行输出一个整数b,代表满足条件的素数对中的较大者。
解题思路:
给定偶数input,从2开始for循环,判断i和input - i是不是都质数,则代表符合题意,从0遍历到给定偶数input/2,最后一个必然是答案
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int input = in.nextInt();
int a = 0;
int b = 0;
for (int i = 2; i <= input / 2; i++) {
if (isPrime(i) && isPrime(input - i)) {
a = i;
b = input - i;
}
}
System.out.println(a);
System.out.println(b);
}
public static boolean isPrime(int a) {
if (a <= 3) {
return true;
}
for (int i = 2; i <= Math.sqrt(a); i++) {
if (a % i == 0) {
return false;
}
}
return true;
}
}HJ61 放苹果
描述:
我们需要将m个相同的苹果放入n个相同的盘子中,允许有的盘子空着不放。求解有多少种不同的分法。
输入描述:
输入两个整数m,n(0≦m≦10; 1≦n≦10)代表苹果数、盘子数。
输出描述:
输出一个整数,代表不同的分法数量。
解题思路:
递归 + 动态规划
一个盘子或者零个苹果,只有一种情况
如果盘子比苹果多,就全都按苹果算,因为肯定会出现空盘子
否则
情况一: 只用 b - 1个盘子,继续递归
情况二: 每个盘子里先放一个苹果,等价于a - b个苹果放到 b 个盘子,继续递归
import java.util.*;
public class Main {
// 递归 + 动态规划
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int appleNum = in.nextInt();
int plateNum = in.nextInt();
System.out.println(count(appleNum, plateNum));
}
public static int count(int appleNum, int plateNum) {
// 一个盘子或者零个苹果,只有一种情况
if (appleNum == 0 || plateNum == 1) {
return 1;
// 如果盘子比苹果多,就全都按苹果算,因为肯定会出现空盘子
} else if (appleNum < plateNum) {
return count(appleNum, appleNum);
} else {
// 情况一: 只用 b - 1个盘子,继续递归
// 情况二: 每个盘子里先放一个苹果,等价于a - b个苹果放到 b 个盘子,继续递归
return count(appleNum, plateNum - 1) + count(appleNum - plateNum, plateNum);
}
}
}HJ62 查找输入整数二进制中1的个数
描述:
对于给定的整数n和m,分别求解他们在二进制表示下的1的个数。
输入描述:
第一行输入一个整数n(0≦n<2³¹)代表需要求解的第一个数字。
第二行输入一个整数m(0≦m<2³¹)代表需要求解的第二个数字。输出描述:
第一行输出一个整数,代表n在二进制表示下的1的个数。
第二行输出一个整数,代表m在二进制表示下的1的个数。
解题思路:
使用Integer类toBinaryString方法转为二进制字符串,然后转为字符数组,然后匹配'1'字符
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
char[] s = Integer.toBinaryString(in.nextInt()).toCharArray();
int result = 0;
for (int i = 0; i < s.length; i++) {
if('1' == s[i]){
result++;
}
}
System.out.println(result);
}
}
}HJ72 百钱买百鸡问题
描述:
公元五世纪,我国古代数学家张丘建在《算经》一书中提出了“百鸡问题”:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
意思是,公鸡一只5元,母鸡一只3元,小鸡三只1元。现在有100元,问公鸡、母鸡、小鸡各多少只?你只需要直接输出答案即可。输入描述:
本题不需要读取输入。
输出描述:
输出若干行,每行包含三个整数,分别代表公鸡、母鸡、小鸡的数量。
解题思路:
暴力循环破解
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
for (int i = 0; i <= 100 / 5; i++) {
for (int j = 0; j <= 100 / 3; j++) {
for (int k = 0; k <= 100 * 3; k += 3) {
if (i * 5 + j * 3 + k / 3 == 100 && i + j + k == 100) {
System.out.println(i + " " + j + " " + k);
}
}
}
}
}
}HJ73 计算日期到天数转换
描述:
每一年中都有12个月份。其中,1,3,5,7,8,10,12月每个月有31天;4,6,9,11月每个月有30天;而对于2月,闰年时有29天,平年时有28天。
现在,对应输入的日期,计算这是这一年的第几天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
- 这个年份是4的整数倍,但不是100的整数倍;
- 这个年份是400的整数倍。
输入描述:
在一行上输入三个整数 a,b,c(1900≦a≦2200),分别代表年、月、日。保证输入的日期是合法的。
输出描述:
输出一个整数,代表输入的日期是这一年的第几天。
解题思路:
使用Calendar类get方法,参数为Calendar.DAY_OF_YEAR
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int year = in.nextInt();
int month = in.nextInt();
int day = in.nextInt();
Calendar calendar = Calendar.getInstance();
calendar.set(year, month - 1, day);
System.out.println(calendar.get(Calendar.DAY_OF_YEAR));
}
}HJ76 尼科彻斯定理
描述:
尼科彻斯定理,又称为斐波那契数列定理,指的是对于任意正整数n,存在一个由连续奇数组成的数列,使得该数列的和等于n的立方。
例如:
- 对于n=1,数列{1}的和为1³=1;
- 对于n=2,数列{3,5}的和为2³=3+5;
- 对于n=3,数列{7,9,11}的和为3³=7+9+11;
- 对于n=4,数列{13,15,17,19}的和为4³=13+15+17+19。
现在,给定一个正整数n,请输出这个数列中的元素从小到大相加的形式。
如果有多个这样的序列,请输出长度为n的那个。
输入描述:
输入一个整数n(1≦n≦100)。
输出描述:
在一行上输出一个字符串,用于描述这个数列中的元素从小到大相加的形式。元素与元素之间用加号连接。
解题思路:
算出输入的数字的立方,再除以n
如果结果为偶数,以该偶数为中心,前后±1,±3,……,按数字大小拼接字符串打印输出
如果结果为奇数,以该奇数为中心,前后±2,±4,……,按数字大小拼接字符串打印输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int n3 = (int) Math.pow(n, 3);
int mid = n3 / n;
String results = "";
if (mid % 2 == 0) {
for (int i = 0; i < n; i++) {
results += mid - 2 * (n / 2 - i) + 1;
results += "+";
}
results = results.substring(0, results.length() - 1);
} else {
for (int i = 0; i < n; i++) {
results += mid - 2 * (n / 2 - i);
results += "+";
}
results = results.substring(0, results.length() - 1);
}
System.out.println(results);
}
}HJ78 小苯送礼物
描述:
小苯是“小红书app”的一名博主,这天他想要给自己的“铁粉”送一些礼物。
他有n名粉丝,编号从1到n,但他只能选择其中k名送礼物,他决定选择其中对他支持力度最大的前k名粉丝。
(如果两名支持力度相同,则优先选择收藏数更多的,如果都一样,则优先选择编号更小的(因为这意味着他关注小苯的时间更早))
具体的:每名粉丝如果每给小苯点一次赞,则他对小苯就增加了1点支持力度,如果他每收藏小苯的一篇文章,则他对小苯增加2点支持力度。
现在小苯想知道,他应该选择哪k名粉丝送出礼物,请你帮帮他吧。输入描述:
输入包含n+1行。
第一行两个正整数n,k(1≤k≤n≤10⁵),分别表示对小苯有过支持的粉丝个数,以及小苯选择送礼的粉丝个数。
接下来n行,每行两个整数xᵢ,yᵢ(0≤xᵢ,yᵢ≤10⁵),表示第i位粉丝给小苯点过x次赞,收藏过y个小苯的文章。输出描述:
输出包含一行k个正整数,表示小苯选择出送礼物的粉丝们的编号。(按照升序输出)
解题思路:
建立实体类,按条件排序,然后根据排序获取用户id打印输出
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
List<Person> personList = new ArrayList<>();
for (int i = 1; i <= n; i++) {
int k1 = in.nextInt();
int k2 = in.nextInt();
personList.add(new Person(i, k1, k2, k1 + k2 * 2));
}
personList.sort((a, b) -> {
if (b.points != a.points) {
return b.points - a.points;
}
if (b.collectNum != a.collectNum) {
return b.collectNum - a.collectNum;
}
return a.id - b.id;
});
int[] id = new int[k];
for (int i = 0; i < k; i++) {
id[i] = personList.get(i).id;
}
Arrays.sort(id);
for (int i = 0; i < k; i++) {
System.out.print(id[i]);
if (i != k - 1) {
System.out.print(" ");
}
}
}
public static class Person {
public int id;
public int likeNum;
public int collectNum;
public int points;
public Person(int id, int likeNum, int collectNum, int points) {
this.id = id;
this.likeNum = likeNum;
this.collectNum = collectNum;
this.points = points;
}
}
}HJ79 支付宝消费打折
描述:
众所周知,在一些消费支付的场合中,往往有“支付宝九五折”的优惠。
这天小苯来到了超市购买物品,一共有n种物品,每种物品只能购买一个,但有的物品支持优惠活动,有的并不支持。恰好本超市的结账是有“支付宝九五折”优惠的,小苯的支付宝余额还剩k元,他想知道他仅使用支付宝进行支付的话,最多能买几件物品?输入描述:
输入包含三行。
第一行两个正整数n,k(1≤n≤10⁵), (1≤k≤10⁹)。
第二行包含n个正整数ai(1≤aᵢ≤10⁴)表示每个物品的价格。
第三行一个长度为n的只含有0和1的字符串,表示每个物品是否支持优惠。(如果是1代表第i个物品支持优惠,否则不支持。)输出描述:
输出一行一个整数表示答案。
解题思路:
根据打折标志,判断商品的最终价格,然后根据最终价格排序,依次获取价格最低的商品,并与预算进行比较,获取商品数量
注意货币计算,原则上不允许用double和float,只能用整数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
long totalAmount = in.nextLong() * 100L;
int[] goodsPrice = new int[count];
List<Long> list = new ArrayList<>();
for (int i = 0; i < count; i++) {
goodsPrice[i] = in.nextInt();
}
char[] alipayFlagArray = in.next().toCharArray();
for (int i = 0; i < count; i++) {
if ('1' == alipayFlagArray[i]) {
list.add(goodsPrice[i] * 95L);
} else {
list.add(goodsPrice[i] * 100L);
}
}
list.sort(null);
long local = 0L;
int result = 0;
for (Long goods : list) {
local += goods;
if (local <= totalAmount) {
result++;
} else {
break;
}
}
System.out.println(result);
}
}HJ80 整型数组合并
描述:
对于给定的由n个整数组成的数组{a₁,a₂,…,aₙ}和m个整数组成的数组{b₁,b₂,…,bₘ},将它们合并后从小到大排序,并输出去重后的结果。
注意,本题在输出时,元素间不需要输出空格。输入描述:
第一行输入一个整数n(1≦n≦150)代表数组a中的元素个数。
第二行输入n个整数a₁,a₂,…,aₙ−1≦aᵢ≦10⁵)代表数组a中的元素。
第三行输入一个整数m(1≦m≦150)代表数组b中的元素个数。
第四行输入m个整数b₁,b₂,…,bₘ(−1≦bᵢ≦10⁵)代表数组b中的元素。输出描述:
输出按升序合并、去重后的数组。
解题思路:
利用TreeSet实现有序去重
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
Set<Integer> set = new TreeSet<>();
int a1 = in.nextInt();
for (int i = 0; i < a1; i++) {
set.add(in.nextInt());
}
int a2 = in.nextInt();
for (int i = 0; i < a2; i++) {
set.add(in.nextInt());
}
for (Integer i : set) {
System.out.print(i);
}
}
}HJ81 字符串字符匹配
描述:
对于给定的字符串s和t,检查s中的所有字符是否都在t中出现。
输入描述:
第一行输入一个长度为1≦len(s)≦200、仅由小写字母组成的字符串s。
第二行输入一个长度为1≦len(t)≦200、仅由小写字母组成的字符串t。输出描述:
如果s中的所有字符都在t中出现,则输出true,否则输出false。
解题思路:
使用String类的contains方法,判断字符是否存在
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] a = in.next().toCharArray();
String b = in.next();
for (int i = 0; i < a.length; i++) {
if (!b.contains(a[i] + "")) {
System.out.println(false);
return;
}
}
System.out.println(true);
}
}HJ84 统计大写字母个数
描述:
对于给定的由可见字符和空格构成的字符串s,统计其中大写字母的个数。
字符串由ASCII码在32到126范围内的字符组成。输入描述:
在一行上输入一个长度为1≦len(s)≦250,由可见字符和空格构成的字符串s。
输出描述:
输出一个整数,表示字符串中大写字母的个数。
解题思路:
字符串转字符数组,遍历字符数组,根据Character类isUpperCase方法判断
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] cs = in.nextLine().toCharArray();
int result = 0;
for (int i = 0; i < cs.length; i++) {
if (Character.isUpperCase(cs[i])) {
result++;
}
}
System.out.println(result);
}
}HJ85 最长回文子串
描述:
对于给定的由小写字母构成的字符串s,求出其最长回文子串的长度。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。
一个字符串被称作回文串,当且仅当这个字符串从左往右读和从右往左读是相同的。输入描述:
在一行上输入一个长度为1≦len(s)≦350、仅由小写字母构成的字符串s。
输出描述:
输出一个整数,表示字符串s的最长回文子串的长度。
解题思路:
从index为0开始,依次以该字符为中心向两边扩展,判断子串两侧字符是否相等,相等扩展子串,继续判断,直到不相等,返回回文长度,判断最长回文长度
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.next();
int max = 0;
for (int i = 0; i < s.length(); i++) {
//奇数长度回文数
int i1 = huiWenShu(s, i, i);
//偶数长度回文数
int i2 = huiWenShu(s, i, i + 1);
//判断最长的回文子串的长度
int i3 = Math.max(i1, i2);
// 如果找到更长的回文,更新
if (i3 > max) {
max = i3;
}
}
System.out.println(max);
}
public static int huiWenShu(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return right - left - 1;
}
}HJ86 求最大连续bit数
描述:
对于给定的十进制整数n,求解其二进制表示中,最长连续1段的长度。
输入描述:
输入一个十进制整数n(1≦n≦5×10⁵)。
输出描述:
输出一个整数,表示n的二进制表示中,最长连续1段的长度。
解题思路:
使用Integer类toBinaryString方法转为二进制字符串,再用"0"分割,计算最长的子串
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] ss = Integer.toBinaryString(in.nextInt()).split("0");
int len = 0;
for (int i = 0; i < ss.length; i++) {
if (ss[i].length() > len) {
len = ss[i].length();
}
}
System.out.println(len);
}
}HJ87 密码强度等级
描述:
密码按如下规则进行计分,并根据不同的得分为密码进行安全等级划分。
一、密码长度:
5分:小于等于4个字符
10分:5到7字符
25分:大于等于8个字符
二、字母:
0分:没有字母
10分:密码里的字母全都是小(大)写字母
20分:密码里的字母符合“大小写混合”
三、数字:
0分:没有数字
10分:1个数字
20分:大于1个数字
四、符号:
0分:没有符号
10分:1个符号
25分:大于1个符号
五、奖励(只能选符合最多的那一种奖励):
2分:字母和数字
3分:字母、数字和符号5分:大小写字母、数字和符号
最后的评分标准:
>=90:非常安全
>=80:安全(Secure)
>=70:非常强
>=60:强(Strong)
>=50:一般(Average)
>=25:弱(Weak)
>=0:非常弱(Very_Weak)
对应输出为:
VERY_SECURE
SECURE
VERY_STRONG
STRONG
AVERAGE
WEAK
VERY_WEAK
请根据输入的密码字符串,进行安全评定。
注:
字母:a-z, A-Z
数字:0-9
符号包含如下:(ASCII码表可以在UltraEdit的菜单view->ASCII Table查看)
!"#$%&'()*+,-./ (ASCII码:0x21~0x2F)
:;<=>?@ (ASCII码:0x3A~0x40)
[\]^_` (ASCII码:0x5B~0x60)
{|}~ (ASCII码:0x7B~0x7E)
提示:
1<=字符串的长度<=300输入描述:
输入一个string的密码
输出描述:
输出密码等级
解题思路:
按照规则,使用Character类isUpperCase,isLowerCase,isDigit,isLetter方法判断
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String password = in.nextLine();
int score = 0;
int len = password.length();
// 判断长度
if (len <= 4) {
score += 5;
} else if (len >= 5 && len <= 7) {
score += 10;
} else if (len >= 8) {
score += 25;
}
int isUpper = 0;
int isLower = 0;
int number = 0;
int other = 0;
// 统计各字母、符号的数量
for (int i = 0; i < password.length(); i++) {
Character c = password.charAt(i);
if (Character.isDigit(c)) {
number++;
} else if (Character.isUpperCase(c)) {
isUpper++;
} else if (Character.isLowerCase(c)) {
isLower++;
} else if (!Character.isDigit(c) && !Character.isLetter(c)) {
other++;
}
}
// 判断字母
if (isLower == 0 && isUpper == 0) {
score += 0;
} else if (isLower > 0 && isUpper > 0) {
score += 20;
} else if (isLower > 0 || isUpper > 0) {
score += 10;
}
// 判断数字
if (number == 0) {
score += 0;
} else if (number == 1) {
score += 10;
} else {
score += 20;
}
//判断符号
if (other == 0) {
score += 0;
} else if (other == 1) {
score += 10;
} else {
score += 25;
}
// 奖励
if (isLower > 0 && isUpper > 0 && number > 0 && other > 0) {
score += 5;
} else if (number > 0 && (isLower > 0 || isUpper > 0) && other > 0) {
score += 3;
} else if (number > 0 && (isLower > 0 || isUpper > 0)) {
score += 2;
}
//输出结果
if (score >= 90) {
System.out.println("VERY_SECURE");
} else if (score >= 80) {
System.out.println("SECURE");
} else if (score >= 70) {
System.out.println("VERY_STRONG");
} else if (score >= 60) {
System.out.println("STRONG");
} else if (score >= 50) {
System.out.println("AVERAGE");
} else if (score >= 25) {
System.out.println("WEAK");
} else if (score >= 0) {
System.out.println("VERY_WEAK");
}
}
}HJ91 走方格的方案数
描述:
对于给定的由n+1条横线和m+1条竖线组成的网格,共相交形成n×m个格点。
现在,你从网格的左上角格点出发,只能沿着网格线向右或向下走,求解走到右下角格点的不同方案数。输入描述:
在一行上输入两个整数n,m(1≦n,m≦8),代表网格的行数和列数。
输出描述:
输出一个整数,代表不同的行走方案数。
解题思路:
动态规划
边上的每一个点的可能性都是1,因为走到边上,就只能顺着边往下走了,可能性只能是1
往后每一个点,都是后面两个点的可能性之和,因为它可以选择任意一个点来走,可能性就是下两个点的可能性相加
最终加到最后一个点,可能性就是所有的路线数量
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
System.out.println(getCount(n, m));
}
public static int getCount(int n, int m) {
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < m + 1; j++) {
if (i == 0 || j == 0) {
// 边上的每一个点的可能性都是1,因为走到边上,就只能顺着边往下走了,可能性只能是1
dp[i][j] = 1;
} else {
// 往后每一个点,都是后面两个点的可能性之和,因为它可以选择任意一个点来走,可能性就是下两个点的可能性相加
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
}
}
}
// 最终加到最后一个点,可能性就是所有的路线数量
return dp[n][m];
}
}HJ94 记票统计
描述:
某场选举一共有n位候选人入选,候选人的名字均由大写字母构成,且互不相同,使用c₁,c₂,…,cₙ表示。
选举结束后,统计了m张选票,每张选票上均写有候选人的名字,使用v₁,v₂,…,vₘ表示。
求解每个候选人获得的票数。特别地,如果某张选票上的候选人名字不在候选名单中,则该票视为无效票。你需要同时统计无效票的数量。输入描述:
第一行输入一个整数n(1≦n≦100)代表候选人数。
第二行输入n个长度为1≦len(cᵢ)≦10、仅由大写字母构成的字符串c₁,c₂,…,cₙ,代表候选人的名字。保证候选人的名字互不相同。
第三行输入一个整数m(1≦m≦100)代表投票人数。
第四行输入m个长度为1≦len(vᵢ)≦10、仅由大写字母构成的字符串v₁,v₂,…,vₘ,代表投票内容。输出描述:
对于每一位候选人,新起一行。先输出其名字,随后输出一个空格、一个冒号、一个空格作为间隔,最后输出其获得的票数。形如cᵢ: numbersᵢ,其中cᵢ是候选人的名字,numbersᵢ是候选人的票数。
最后一行以相同的格式输出无效票的数量。形如Invalid : numbers,其中numbers是无效票的数量。
解题思路:
使用LinkedHashMap,LinkedHashMap按插入顺序排序
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
Map<String, Integer> map = new LinkedHashMap<>();
for (int i = 0; i < a; i++) {
map.put(in.next(), 0);
}
map.put("Invalid", 0);
int b = in.nextInt();
for (int i = 0; i < b; i++) {
String s = in.next();
if (map.get(s) != null) {
map.put(s, map.get(s) + 1);
} else {
map.put("Invalid", map.get("Invalid") + 1);
}
}
for (String key : map.keySet()) {
System.out.println(key + " : " + map.get(key));
}
}
}HJ95 小心火烛的歪
描述:
小歪正在一个占地n×m大小的草地上研究他的燃放烟花计划。其中,一些位置已经堆放了杂物,为了便于观察,我们将给出一个n×m大小的字符矩阵描述草地。其中,堆放了杂物的位置使用数字1标注;其余位置使用数字0标注。
小歪已经做好了若干个烟花燃放计划,每一个计划均为一个n×m大小的字符矩阵,一一对应草地的每一个方格。在这个计划中,将会被燃放烟花的地块使用数字1标注;没有烟花的地块使用数字0标注。
他想选择一些计划同时实施,如果某个地块在任意一个计划中被标注为燃放,那么这个地块就会真的燃放上烟花。小歪想要知道,是否存在这样一种选择方法,使得全部有杂物位置均不会燃放烟花,而没有杂物的位置全部燃放上烟花;如果存在,请输出最少数量的计划。输入描述:
第一行输入三个整数n,m,q(1≦n,m,q≦7)代表草地的长、草地的宽、计划数量。
此后n行,每行输入m个字符,代表草地初始状态。
此后n×q行,每行输入m个字符,用于描述计划。
全部字符仅为数字0或1 。输出描述:
如果不存在满足要求的燃放方案,直接输出−1 。
否则,请按如下格式输出:
第一行上输出一个整数p(0≦p≦q)代表使用到的计划数量。
第二行输出p个整数代表你所选择的计划编号。编号即输入顺序,从1开始计数。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。
解题思路:
枚举所有非空子集(从 0 到 2𐞥−1),用二进制位表示是否选择某个计划
对每个子集:初始化一个 n×m 的结果矩阵 result,全 0。对每个被选中的计划,将 result 与计划矩阵做按位或。
对于grid[i][j] == 1(有杂物)的位置,要求 result[i][j] == 0。
对于grid[i][j] == 0(无杂物)的位置,要求 result[i][j] == 1。
如果满足条件,记录该子集的大小(计划数)和具体选择。
取计划数最小的子集输出,如果多个最小,任意一个即可。
如果没有满足条件的子集,输出 -1。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
// 读入草地
int[][] grid = new int[n][m];
for (int i = 0; i < n; i++) {
String line = in.next();
for (int j = 0; j < m; j++) {
grid[i][j] = line.charAt(j) - '0';
}
}
// 读入计划
int[][][] plans = new int[q][n][m];
for (int k = 0; k < q; k++) {
for (int i = 0; i < n; i++) {
String line = in.next();
for (int j = 0; j < m; j++) {
plans[k][i][j] = line.charAt(j) - '0';
}
}
}
int minSize = Integer.MAX_VALUE;
int bestMask = -1;
// 枚举所有子集 (mask 从 1 到 2𐞥-1,0 表示不选任何计划,但可能不满足无杂物位置燃放要求)
for (int mask = 0; mask < (1 << q); mask++) {
int[][] result = new int[n][m];
// 应用选中的计划(按位或)
for (int k = 0; k < q; k++) {
if (((mask >> k) & 1) == 1) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
result[i][j] |= plans[k][i][j];
}
}
}
}
// 检查条件
boolean valid = true;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
// 有杂物位置不能燃放
if (result[i][j] != 0) {
valid = false;
break;
}
} else {
// 无杂物位置必须燃放
if (result[i][j] != 1) {
valid = false;
break;
}
}
}
if (!valid) break;
}
if (valid) {
int size = Integer.bitCount(mask);
if (size < minSize) {
minSize = size;
bestMask = mask;
}
}
}
if (bestMask == -1) {
System.out.println(-1);
} else {
// 输出结果
System.out.println(minSize);
boolean first = true;
for (int k = 0; k < q; k++) {
if (((bestMask >> k) & 1) == 1) {
if (first) {
System.out.print(k + 1);
first = false;
} else {
System.out.print(" " + (k + 1));
}
}
}
System.out.println();
}
}
}HJ96 表示数字
描述:
对于给定的由字母和数字混合构成的字符串s,找到全部的连续数字子串,并在每一个子串的前后添加星号(*);其余字符保持不变。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。输入描述:
在一行上输入一个长度为1≦len(s)≦100、由大小写字母和数字混合构成的字符串s。
输出描述:
在一行上输出处理后的字符串s。
解题思路:
字符串转字符数组,遍历数组,按规则添加*
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] ca = in.next().toCharArray();
StringBuffer sb = new StringBuffer();
for (int i = 0; i < ca.length; i++) {
// 如果字符是数字
if (Character.isDigit(ca[i])) {
// 位置在开头,或者前面的字符不是数字,添加*
if (i == 0) {
sb.append("*");
} else if (!Character.isDigit(ca[i - 1])) {
sb.append("*");
}
sb.append(ca[i]);
// 位置在结尾,或者后面的字符不是数字,添加*
if (i == ca.length - 1) {
sb.append("*");
} else if (!Character.isDigit(ca[i + 1])) {
sb.append("*");
}
} else {
sb.append(ca[i]);
}
}
System.out.println(sb);
}
}HJ97 记负均正
描述:
对于给定的n个整数a₁,a₂,…,aₙ,统计并计算:
- 负整数的个数;
- 正整数的平均值。
输入描述:
第一行输入一个整数n(1≦n≦2×10³)代表整数的个数。
第二行输入n个整数a₁,a₂,…,aₙ(−10³≦ai≦10³)代表输入的整数。输出描述:
先输出一个整数,代表负整数的个数;随后在同一行输出一个实数,代表正整数的平均值。
由于实数的计算存在误差,当误差的量级不超过10⁻⁶)时,您的答案都将被接受。具体来说,设您的答案为a,标准答案为b,当且仅当∣a−b∣/max(1,∣b∣)≦10⁻⁶时,您的答案将被接受。
解题思路:
按题目要求,负数计算数量,正数求平均值
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int negativeCount = 0;
double positive = 0;
int positiveCount = 0;
for (int i = 0; i < a; i++) {
int temp = in.nextInt();
if (temp < 0) {
negativeCount++;
} else if (temp > 0) {
positive += temp;
positiveCount++;
}
}
if (positiveCount == 0) {
System.out.print(negativeCount + " " + 0);
} else {
System.out.print(negativeCount + " " + positive / positiveCount);
}
}
}HJ99 自守数
描述:
自守数是指这样一个自然数x,其平方的尾数等于自身。更具体的说,即x²的末尾若干位恰好等于x,例如:
25²=625,625的末尾两位恰好是25;
76²=5776,5776的末尾两位恰好是76;
9376²=87909376,87909376的末尾四位恰好是9376。
现在,对于给定的n,请统计0到n之间的自守数个数。输入描述:
输入一个整数n(1≦n≦10⁴)代表自守数的范围。
输出描述:
输出一个整数,代表0到n之间的自守数个数。
解题思路:
用String类endsWith方法计算自守数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int result = 0;
for (int i = 0; i <= a; i++) {
String x2s = Integer.toString(i * i);
if (x2s.endsWith(i + "")) {
result++;
}
}
System.out.println(result);
}
}HJ100 等差数列
描述:
对于首项为2,公差为3的等差数列,求前n项的和。
输入描述:
输入一个整数n(1≦n≦10³)。
输出描述:
输出一个整数,代表前n项的和。
解题思路:
可以用等差数列公式,也可以直接累加
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int temp = 2;
int result = 2;
for (int i = 1; i < a; i++) {
temp += 3;
result += temp;
}
System.out.println(result);
}
}HJ102 字符统计
描述:
对于给定的由小写字母和数字构成的字符串s,统计出现的每一个字符的出现次数,按出现次数从多到少排序后依次输出。特别地,如果出现次数相同,则按照ASCII码由小到大排序。
输入描述:
在一行上输入一个长度为1≦len(s)≦10³、由小写字母和数字构成的字符串s。
输出描述:
在一行上输出一个字符串,代表按频次统计后的结果。
解题思路:
建立实体类,计算字符出现次数,然后按次数倒序和ascii码正序排序打印
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] ca = in.next().toCharArray();
Map<Character, Integer> map = new TreeMap<>();
for (int i = 0; i < ca.length; i++) {
map.put(ca[i], map.getOrDefault(ca[i], 0) + 1);
}
List<Order> orderList = new ArrayList<>();
for (Character key : map.keySet()) {
orderList.add(new Order(key, map.get(key)));
}
orderList.sort((a, b) -> {
if (a.count != b.count) {
return b.count - a.count;
} else {
return a.letter - b.letter;
}
});
for (Order c : orderList) {
System.out.print(c.letter);
}
}
public static class Order {
public char letter;
public int count;
public Order(char letter, int count) {
this.letter = letter;
this.count = count;
}
}
}HJ106 字符逆序
描述:
对于给定的由小写字母和空格混合构成的字符串s,将其翻转后输出。
保证给定的字符串s的首尾不为空格。输入描述:
在一行上输入一个长度为1≦len(s)≦10⁴、由小写字母和空格混合构成的字符串s。
输出描述:
输出一个字符串,表示将输入字符串s翻转后的结果。
解题思路:
使用StringBuffer类reverse方法
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
StringBuffer sb = new StringBuffer(in.nextLine());
System.out.print(sb.reverse());
}
}HJ108 求最小公倍数
描述:
对于给定的两个正整数a,b,它们的最小公倍数lcm(a,b)是指能同时被a和b整除的最小正整数。
求解lcm(a,b)。输入描述:
在一行上输入两个整数a,b(1≦a,b≦10⁵)。
输出描述:
输出一个整数,表示lcm(a,b)。
解题思路:
乘积除以最大公约数,等于最小公倍数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int j = m * n;
if (n > m) {
int temp = m;
m = n;
n = temp;
}
//最大公约数
while (n != 0) {
int r = m % n;
m = n;
n = r;
}
int max = j / m;
System.out.println(max);
}
}HJ109 最小循环节
描述:
给定一个长度为n、由大小写字母混合构成的字符串s,你可以无限次的往字符串的任何地方插入任意字符。求新字符串s的最小循环节。
对于字符串b,找到最短长度的子串a,使得字符串b是由子串a拼接若干次得到的,即b=aa⋯a。这里的子串a的长度即为字符串b的最小循环节。
输入描述:
在一行上输入一个长度不超过10⁵、由大小写字母混合构成的字符串s,代表初始字符串。
输出描述:
在一行上输出一个整数,代表字符串s的最小循环节的长度。
解题思路:
本质就是求字符个数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextLine()) {
String str = in.nextLine();
HashSet<Character> set = new HashSet<>();
for (char c : str.toCharArray()) {
set.add(c);
}
System.out.println(set.size());
}
}
}HJ110 宝石手串
描述:
小红有一个n颗宝石构成的环形宝石手串,即第一颗和最后一颗宝石相连,其中第i个宝石的属性为sᵢ;若两个宝石的属性相同,那么这两个宝石会相互排斥,导致断开。
小红可以从手串中摘掉一些宝石,每次摘掉后,这个宝石左右的两个宝石会相接,手串依旧是环形。小红想要破坏这个手串。她想要知道,最少还需要摘掉多少个宝石才会导致手串断开。特别的,当手串上剩余的宝石数量恰好为2而依旧没能断开时,视为破坏失败,直接输出−1 。
输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦100)代表数据组数,每组测试数据描述如下:
第一行输入一个整数n(2≦n≦10⁵)代表手串初始的宝石数量。
第二行输入一个长度为n、仅由小写字母构成的字符串,代表手串上每个宝石的属性。
除此之外,保证单个测试文件的n之和不超过10⁵。
输出描述:
对于每一组测试数据,如果手环无法破坏,直接输出−1;否则,在一行上输出一个整数,代表手串断开需要的最少操作次数。
解题思路:
把字符串复制一份拼接,然后计算相同的字符,出现的最小间距,如果没有相同字符,则最小间距为字符串长度-1,返回-1
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int T = in.nextInt();
for (int i = 0; i < T; i++) {
int n = in.nextInt();
String s = in.next();
String str = s + s;
Map<Character, Integer> map = new HashMap<>();
char[] chars = str.toCharArray();
int min = Integer.MAX_VALUE;
for (int j = 0; j < chars.length; j++) {
if (map.containsKey(chars[j])) {
min = Math.min(min, j - map.get(chars[j]) - 1);
}
map.put(chars[j], j);
}
if (min == s.length() - 1) {
System.out.println(-1);
} else {
System.out.println(min);
}
}
}
}HJ115 小红的区间构造
描述:
小红拿到了正整数x,她希望你找到一个长度为k的区间,满足区间内恰好有n个数是x的倍数。你能帮帮她吗?
输入描述:
在一行上输入三个整数n,k,x(1≤n,k,x≤10⁹)。
输出描述:
如果答案不存在,直接输出−1;否则,输出两个正整数l,r(1≤l≤r<2×10⁹;l+k−1=r)代表答案。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。
解题思路:
如果n乘x小于等于给的区间长度k,直接把区间设置为1到k
如果n乘x小于0,返回-1
如果(n - 1) * x小于等于k,直接把区间设置为x到x + k - 1
否则返回-1
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
long n = in.nextLong();
long k = in.nextLong();
long x = in.nextLong();
long s = n * x;
if (s <= k) {
System.out.println(1 + " " + k);
return;
}
if (s < 0) {
System.out.println(-1);
return;
}
long temp = (n - 1) * x;
if (temp <= k) {
System.out.println(x + " " + (x + k - 1));
return;
}
System.out.println(-1);
}
}HJ121 球格模型(简单版)
描述:
对于n行m列的网格,一共有n×m个格子。
现在,一共有k个小球,小球需要全部放入格子中,单个格子可以放置多个小球,也可以不放。
你只需要输出任意一种符合条件的摆放方式;使得任意行、任意列均至少有一个小球。特别地,如果不存在这样的摆放方式,直接输出−1 。输入描述:
在一行上输入三个整数n,m,k(1≦n,m,k≦10⁶;n×m≦10⁶)代表网格的行数、网格的列数、小球数量。
输出描述:
如果不存在符合条件的摆放方式,直接输出−1 ;否则,输出n行m列的矩阵,代表一种符合条件的摆放方式。矩阵第i行第j列的元素aᵢ,ⱼ(0≦aᵢ,ⱼ≦k)代表第i行第j列的格子中放置的小球数量。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。
解题思路:
先按对角线,依次放一个,如果有剩余,行数大于列数,就给剩余列第一行放1个,列数大于行数,就给剩余行第一列放1个,如果还有剩余,放在第一行第一列,如果数量不足行或列最小值,返回-1
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int b = in.nextInt();
int c = in.nextInt();
int max = Math.max(a, b);
int min = Math.min(a, b);
if (c < max) {
System.out.println(-1);
return;
}
int[][] array = new int[a][b];
for (int i = 0; i < max; i++) {
if (i < min) {
array[i][i] = 1;
c -= 1;
} else {
if (a > b) {
array[i][0] = 1;
c -= 1;
} else if (b > a) {
array[0][i] = 1;
c -= 1;
}
}
}
if (c != 0) {
array[0][0] += c;
}
for (int i = 0; i < a; i++) {
String s = "";
for (int j = 0; j < b; j++) {
s += array[i][j];
s += " ";
}
System.out.println(s.trim());
}
}
}HJ122 小数字
描述:
小娴给阿笙出了一种简单数学题,小娴给出数字n,并规定三种操作:
若n为非负整数,开根号(向上取整),即 n→⌈√n⌉ ;
对当前的数字n减1,即n→n−1;
对当前数字除以2(向上取整),即 n→⌈n/2⌉;
现在可以对数字n操作m次,小娴想让阿笙计算出操作m次之后n最小可以为多少。输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦2×10⁵)代表数据组数,每组测试数据描述如下:
在一行上输入两个整数n,m(1≦n,m≦10⁹)代表初始数字、操作次数。输出描述:
对于每一组测试数据,在单独的一行上输出一个整数,代表操作m次之后n最小可以为多少。
解题思路:
按题目进行计算,for循环中,如果t1小于3,则直接算结果
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
for (int i = 0 ; i < count ; i ++) {
int c1 = in.nextInt();
int c2 = in.nextInt();
int t1 = c1;
int t2 = c1;
for (int j = 0 ; j < c2 ; j++) {
if (t1 >= 3) {
t1 = (int)Math.sqrt(t2);
// 开方后如果是整数,则表明相乘为原开方数,继续循环,如果不是,则+1
if (t1 * t1 != t2) {
t1 ++;
}
t2 = t1;
} else {
t1 = t1 - c2 + j;
break;
}
}
System.out.println(t1);
}
}
}HJ123 预知
描述:
牌桌上有n种不同的卡牌,第i种卡牌有ai张。初始时,所有的卡牌均背面朝上,但不知道其确切的种类。你有两次翻牌机会,翻牌后,如果两张卡牌种类一致,那你就输了。两次翻牌同时进行(不存在根据翻开的第一张牌更改策略的情况)。
你不喜欢运气游戏,所以你可以通过手段随机预知k张卡牌后再进行游玩。
然而,预知很累!你想要知道,你至少需要预知多少张卡牌,才能保证你不会输。输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦2×10⁵)代表数据组数,每组测试数据描述如下:
第一行输入一个整数n(1≦n≦2×10⁵)代表卡牌种类数。
第二行输入n个整数a₁,a₂,…,aₙ(1≦ai≦10⁹)代表每种卡牌数量。
除此之外,保证每一组测试数据的卡牌总数之和不小于2;单个测试文件的n之和不超过2×10⁵。输出描述:
对于每一组测试数据,如果没有必胜策略,直接输出−1;否则,在单独的一行上输出一个整数,代表你至少需要预知多少张卡牌,才能保证你不会输。
解题思路:
按照卡牌类型,卡牌数量,只有1张牌的种类的数量进行判断
如果只有一种类型,则为-1
如果只有两张牌,则为0
如果只有1张牌的种类,为总种类-1,则为出现的牌中种类最多的牌的数量-1
否则就是出现的牌中种类最多的牌
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
for (int i = 0; i < count; i++) {
int type = in.nextInt();
int[] array = new int[type];
int total = 0;
int max = 0;
int oneCardTypeCount = 0;
for (int j = 0; j < type; j++) {
array[j] = in.nextInt();
if (array[j] > max) {
max = array[j];
}
if (array[j] == 1) {
oneCardTypeCount++;
}
total += array[j];
}
// 如果只有一种类型,则为-1
if (type == 1) {
System.out.println(-1);
continue;
}
// 如果只有两张牌,则为0
if (total == 2) {
System.out.println(0);
continue;
}
// 如果只有1张牌的种类,为总种类-1,则为出现的牌中种类最多的牌的数量-1
if (oneCardTypeCount == type - 1) {
System.out.println(max - 1);
continue;
}
// 否则就是出现的牌中种类最多的牌
System.out.println(max);
}
}
}HJ127 小红的双生串
描述:
小红定义一个字符串是双生串,当且仅当其前半部分所有字符相同,后半部分所有字符相同。
现在,小红拿到了一个字符串s ,她每次操作可以修改一个字符。小红希望你求出将其修改为双生串的最小修改次数。输入描述:
在一行上输入一个长度为1≦len(s)≦2×10⁵且为偶数,仅由小写字母构成的字符串s,代表待修改的字符串。
输出描述:
输出一个整数,表示将s修改为双生串的最小修改次数。
解题思路:
分后两段遍历,获取两段中出现最多的字符的次数,然后总数减去这两个最多的次数
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] ca = in.next().toCharArray();
Map<Character, Integer> map1 = new HashMap<>();
for (int i = 0; i < ca.length / 2; i++) {
map1.put(ca[i], map1.getOrDefault(ca[i], 0) + 1);
}
Map<Character, Integer> map2 = new HashMap<>();
for (int i = ca.length / 2; i < ca.length; i++) {
map2.put(ca[i], map2.getOrDefault(ca[i], 0) + 1);
}
int max1 = 0;
int max2 = 0;
for (Character key : map1.keySet()) {
if (map1.get(key) > max1) {
max1 = map1.get(key);
}
}
for (Character key : map2.keySet()) {
if (map2.get(key) > max2) {
max2 = map2.get(key);
}
}
System.out.println(ca.length - max1 - max2);
}HJ131 数独数组
描述:
对于给定的由n个整数组成的数组{a₁,a₂,…,aₙ},我们称其为数独数组,当且仅当其每一个长度为9的连续子数组,都包含1∼9这9个数字。
现在,对于给定的数组,是否存在一种方案,使得其经过重新排序后成为数独数组?如果是,直接输出YES;否则,输出NO。注意,您不必给出具体的排序方案。输入描述:
第一行输入一个整数n(9≦n≦10⁵)代表数组中的元素数量。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦9)代表数组元素。输出描述:
如果数组在重新排序后可以成为数独数组,输出YES;否则,输出NO。
解题思路:
遍历数字,如果数字大于9或者小于0,返回NO,否则加入数组,数组记录数字出现的次数
对数组排序,出现次数最多的在数组尾部,出现次数最少的在数组首部,如果某个数字没有出现,则数组首元素为0,返回NO,然后数组尾部首部相减,如果相差超过2,返回NO,否则返回YES
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int[] ia = new int[a];
for (int i = 0; i < a; i++) {
ia[i] = in.nextInt();
}
int[] match = {0, 0, 0, 0, 0, 0, 0, 0, 0};
for (int i = 0; i < a; i++) {
if (ia[i] > 9 || ia[i] < 0) {
System.out.print("NO");
return;
}
match[ia[i] - 1]++;
}
Arrays.sort(match);
if (match[0] == 0) {
System.out.print("NO");
return;
}
if (match[8] - match[0] > 1) {
System.out.print("NO");
return;
}
System.out.print("YES");
}
}HJ136 翻之
描述:
对于给定的n行m列的矩阵,每一个元素要么是‘0’,要么是‘1’。
每一轮,你可以进行一次以下操作:
- 选择一行的元素,将其全部反置,即‘0’ 变为‘1’,‘1’ 变为‘0’。
请你帮助小歪判断,若能进行任意多轮操作(也可以不进行操作),至多能使得多少列的元素均为‘1’。你只需要输出这个最大值。
输入描述:
第一行输入两个正整数n,m(1≦n,m≦3×10³)代表矩阵的行数和列数。
此后n行,每行输入一个长度为m、仅由‘0’ 和‘1’ 构成的字符串,代表矩阵每一行中的元素。输出描述:
输出一个整数,表示至多能使得多少列的元素均为‘1’。
解题思路:
先获取矩阵,然后获取矩阵列字符串,统计相同字符串出现次数,出现最多的就是结果
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int b = in.nextInt();
int max = 0;
char[][] cat = new char[a][b];
for (int i = 0; i < a; i++) {
char[] ca = in.next().toCharArray();
cat[i] = ca;
}
Map<String, Integer> map = new HashMap<>();
for (int i = 0; i < b; i++) {
StringBuffer sb = new StringBuffer();
for (int j = 0; j < a; j++) {
sb.append(cat[j][i]);
}
String s = sb.toString();
map.put(s, map.getOrDefault(s, 0) + 1);
}
for (String key : map.keySet()) {
if (map.get(key) > max) {
max = map.get(key);
}
}
System.out.println(max);
}
}HJ144 小红书推荐系统
描述:
小红书有一个推荐系统,可以根据用户搜索的关键词推荐用户希望获取的内容。
现在给定小红的搜索记录(记录为分词后的结果),我们认为当一个单词出现的次数不少于3次时,该单词为“用户期望搜索的单词”,即称为关键词。请你根据小红的记录,输出小红的用户画像对应的所有关键词。输入描述:
一行字符串,仅由小写字母和空格组成。代表小红的搜索记录。
字符串长度不超过100000。输出描述:
小红所有的关键词。每行输入一个。你需要按照搜索频次从高到低输出。频次相同的,你需要按字典序升序输出。
解题思路:
字符串拆分,建立实体类,过滤出现次数小于3的字符,然后用list方法排序
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] sa = in.nextLine().split(" ");
List<Word> list = new ArrayList<>();
Map<String, Integer> map = new HashMap<>();
for (String s : sa) {
map.put(s, map.getOrDefault(s, 0) + 1);
}
for (String key : map.keySet()) {
if (map.get(key) >= 3) {
list.add(new Word(key, map.get(key)));
}
}
list.sort((a, b) -> {
if (a.count != b.count) {
return b.count - a.count;
} else {
return a.name.compareTo(b.name);
}
});
for (Word w : list) {
System.out.println(w.name);
}
}
public static class Word {
public String name;
public int count;
public Word(String name, int count) {
this.name = name;
this.count = count;
}
}
}HJ145 小红背单词
描述:
小红每天都要背单词,然后她会把每天记住了多少单词记录下来,并在小红书上打卡。
当小红背单词时,如果她已经记住了i个单词,且背了一个没有记住的新单词i+1次,则她就会记住这个新的单词。
例如,当她按顺序背["you","thank","thank"]时,她第一次背单词"you"时她就能记住"you"。而由于她已经记住了一个单词,所以需要背两次"thank"才能记住"thank"。
现在你知道了小红背单词的顺序,请你求出小红今天记住了多少个单词。
输入描述:
第一行一个整数n(1≤n≤10000)。
接下来n行,每行一个字符串,保证每个字符串长度不超过10。输出描述:
输出一个整数,表示她记住了多少个单词。
解题思路:
Set记录记住的单词,Map记录背诵中的单词的次数,最后获取Set的大小
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = Integer.parseInt(in.nextLine());
// 存储已经记住的单词
Set<String> mem = new HashSet<>();
// 记录单词背诵次数
Map<String, Integer> cntMap = new HashMap<>();
for (int i = 0; i < n; i++) {
String word = in.nextLine();
// 已经记住不再重复记
if (!mem.contains(word)) {
int cnt = cntMap.getOrDefault(word, 0) + 1;
// 记住单词 word
if (cnt > mem.size()) {
mem.add(word);
} else {
cntMap.put(word, cnt);
}
}
}
System.out.println(mem.size());
}
}HJ148 迷宫寻路
描述:
旺仔哥哥被困在一个n×m的矩形迷宫里。每个格子要么是空地 (用符号 `.` 表示),要么是墙 (用符号 `#` 表示)。旺仔哥哥只能从一个空地移动到其上下左右相邻的空地。
已知旺仔哥哥的起点为左上角(1,1),终点为右下角(n,m)。请判断他是否能够到达终点。输入描述:
第一行输入两个正整数n,m(1≦n,m≦100)。
接下来的n行每行输入一个长为m的仅包含字符 `.` 与 `#` 的字符串,描述整个迷宫。
保证起点(1,1)和终点(n,m)均为空地。输出描述:
若旺仔哥哥可以走到终点,则输出单词Yes;否则输出No。
解题思路:
深度优先遍历迷宫
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
char[][] g = new char[n][m];
for (int i = 0; i < n; i++) {
g[i] = in.next().toCharArray();
}
System.out.println(dfs(g, 0, 0) ? "Yes" : "No");
}
private static boolean dfs(char[][] g, int x, int y) {
int row = g.length;
int col = g[0].length;
if (x < 0 || x >= row || y < 0 || y >= col || g[x][y] == '#') {
return false;
}
if (x == row - 1 && y == col - 1) {
return true;
}
g[x][y] = '#';
return dfs(g, x - 1, y) || dfs(g, x, y + 1) || dfs(g, x + 1, y) || dfs(g, x, y - 1);
}
}HJ149 数水坑
描述:
由于降雨,水在农夫约翰的田地里积聚成水坑。田地是一个N×M的矩形网格,每个格子要么是水`W`,要么是干地`.`。
若两个水格子在 八连通 (上下左右及四条对角线)意义下互达,则它们属于同一个水坑。
给出田地示意图,计算水坑数量。输入描述:
第一行输入两个整数N,M(1≦N,M≦100)。
接下来N行,每行M个字符组成的字符串,字符集为`W` 与 `.`,中间无空格。输出描述:
输出一行一个整数,即水坑的数量。
解题思路:
八联通,深度优先遍历
import java.util.*;
public class Main {
// 八联通,深度优先遍历
static int n, m;
static char[][] grid;
static boolean[][] visited;
// 八连通方向:上、下、左、右、左上、右上、左下、右下
static int[] dx = {-1, 1, 0, 0, -1, -1, 1, 1};
static int[] dy = {0, 0, -1, 1, -1, 1, -1, 1};
// 八连通 深度优先遍历
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
grid = new char[n][m];
visited = new boolean[n][m];
for (int i = 0; i < n; i++) {
grid[i] = in.next().toCharArray();
}
int pondCount = 0;
// 遍历整个网格
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 找到未访问的水格子,开始DFS
if (grid[i][j] == 'W' && !visited[i][j]) {
// 标记整个水坑为已访问
dfs(i, j);
// 水坑数量+1
pondCount++;
}
}
}
System.out.println(pondCount);
}
// DFS递归函数
static void dfs(int x, int y) {
// 1. 标记当前格子为已访问
visited[x][y] = true;
// 2. 尝试八个方向
for (int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
// 3. 检查新位置是否有效
if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] == 'W' && !visited[nx][ny]) {
// 4. 递归探索相邻的水格子
dfs(nx, ny);
}
}
}
}HJ150 全排列
描述:
给定一个整数n,请按字典序输出数字1∼n的所有排列。
输入描述:
一行一个整数n(1≦n≦9)。
输出描述:
按字典序输出所有排列,每行输出n个整数,数字之间用单个空格分隔。
解题思路:
全排列算法
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int number = in.nextInt();
List<Integer> list = new ArrayList<>(number);
for (int i = 1; i <= number; i++) {
list.add(i);
}
process(new ArrayList<>(), list);
}
private static void process(List<Integer> x, List<Integer> y) {
if (y.isEmpty()) {
for (Integer i : x) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < y.size(); i++) {
List<Integer> a = new ArrayList<>(x);
List<Integer> b = new ArrayList<>(y);
a.add(b.remove(i));
process(a, b);
}
}
}HJ156 走迷宫
描述:
给定一个n×m的网格。你从起点(xₛ,yₛ)出发,每一次可以向上、下、左、右移动一步(若不超出边界)。某些格子上存在障碍物,无法经过。求从(xₛ,yₛ)移动到终点(xₜ,yₜ)的最少步数;若无法到达,输出−1。
输入描述:
在一行上输入两个整数n,m(1≦n,m≦1000),代表网格的行数与列数。
在一行上输入四个整数xₛ,yₛ,xₜ,yₜ(1≦xₛ,xₜ≦n; 1≦yₛ,yₜ≦m),代表起点与终点的坐标。
此后n行,第i行输入一个长度为m的字符串gi,其中
若 g(i,j)="*",表示第i行第j列为障碍物;
若 g(i,j)=".",表示该格子可通行。
保证起点所在格子可通行。输出描述:
输出一个整数,表示最少移动次数;若无法到达,输出−1。
解题思路:
广度优先搜索(BFS) 遍历迷宫
import java.util.*;
public class Main {
static int n, m, x2, y2 = 0;
static int[] dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
// 广度优先搜索(BFS) 遍历迷宫
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] s1 = in.nextLine().split(" ");
n = Integer.parseInt(s1[0]);
m = Integer.parseInt(s1[1]);
String[] s2 = in.nextLine().split(" ");
int x1 = Integer.parseInt(s2[0]) - 1;
int y1 = Integer.parseInt(s2[1]) - 1;
x2 = Integer.parseInt(s2[2]) - 1;
y2 = Integer.parseInt(s2[3]) - 1;
char[][] grid = new char[n][m];
for (int i = 0; i < n; i++) {
grid[i] = in.nextLine().toCharArray();
}
if (grid[x1][y1] != '.' || grid[x2][y2] != '.') {
System.out.println(-1);
return;
}
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{0, x1, y1});
while (!queue.isEmpty()) {
int[] poll = queue.poll();
int step = poll[0], x = poll[1], y = poll[2];
if (x == x2 && y == y2) {
System.out.println(step);
return;
}
for (int i = 0; i < 4; i++) {
int xx = x + dx[i];
int yy = y + dy[i];
if (check(grid, xx, yy)) {
queue.add(new int[]{step + 1, xx, yy});
grid[xx][yy] = '/';
}
}
}
System.out.println(-1);
}
private static boolean check(char[][] grid, int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || grid[x][y] != '.') {
return false;
}
return true;
}
}HJ157 剪纸游戏
描述:
小蓝拿着一张n×m的方格纸从中剪下若干不相连的图案;剪裁时只会沿着方格网线裁切,因此不会破坏任何一个完整的小方格。
小灰灰只拿到了剩余的残缺纸张。若用`'.'`表示被剪去的小方格,`'*'`表示仍保留的小方格,则他得到一张由`'.'`与`'*'`组成的矩阵。由于各个剪下的图案之间互不连通,小灰灰可以根据 `'.'`的连通块反推出每一个被剪下来的图案。
现在小灰灰想知道:在所有被剪下来的图案中,有多少个是长方形(正方形视为特殊的长方形)。输入描述:
第一行输入两个整数n,m(1≦n,m≦1000)——纸张的行数与列数。
接下来n行,每行输入一个长度为m的由`'.'`与`'*'`组成的字符串,描述残缺纸张的形状:
- `'.'`代表该方格已被剪去;
- '*'`代表该方格仍保留。
输出描述:
输出一个整数,表示被剪下来的图案中长方形的数量。
解题思路:
实际是深度优先遍历(DFS),然后获取最大和最小x,y值,然后判断相乘是否等于面积,即方格数量
import java.util.*;
public class Main {
private static int MaxX, MaxY, MinX, MinY;
// 实际是DFS
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
char[][] g = new char[n][m];
for (int i = 0; i < n; i++) {
g[i] = in.next().toCharArray();
}
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (g[i][j] == '.') {
MaxX = MaxY = 0;
MinX = MinY = 1000;
int s = dfs(g, i, j);
if ((MaxX - MinX + 1) * (MaxY - MinY + 1) == s) {
res++;
}
}
}
}
System.out.print(res);
}
private static int dfs(char[][] g, int x, int y) {
int row = g.length;
int col = g[0].length;
if (x < 0 || y < 0 || x >= row || y >= col || g[x][y] == '*') {
return 0;
}
MaxX = Math.max(MaxX, x);
MaxY = Math.max(MaxY, y);
MinX = Math.min(MinX, x);
MinY = Math.min(MinY, y);
g[x][y] = '*';
return 1 + dfs(g, x - 1, y) + dfs(g, x + 1, y) + dfs(g, x, y - 1) + dfs(g, x, y + 1);
}
}HJ158 挡住洪水
描述:
吴铭市近日洪水肆虐,洪水从地图外部渗入。市政部门在若干方格上砌起围墙,用`*`表示。若某片空地区域不与地图边界四联通(上下左右方向),则不会被洪水淹没,视为安全空地。
地图用大小为x×y的字符矩阵描述:`'*'`表示围墙,`'0'`表示空地。所有相互四联通的`'0'`构成一个区域。请统计所有安全空地格子的数量之和(即所有不与边界四联通的`'0'`的总数)。输入描述:
第一行输入两个整数x,y(1≦x,y≦500)。
接下来x行,每行y个字符,组成围墙建设图,仅含`'*'`与`'0'`。输出描述:
输出一个整数,表示所有安全空地格子的总数。
解题思路:
实际是深度优先遍历(DFS),从四周开始,将洪水可以到达的地方标记,然后继续遍历剩余的空地,得到空地数量
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
char[][] g = new char[n][m];
for (int i = 0; i < n; i++) {
g[i] = in.next().toCharArray();
}
for (int i = 0; i < n; i++) {
dfs(g, i, 0);
dfs(g, i, m - 1);
}
for (int j = 0; j < m; j++) {
dfs(g, 0, j);
dfs(g, n - 1, j);
}
int res = 0;
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < m - 1; j++) {
if (g[i][j] == '0') {
res += dfs(g, i, j);
}
}
}
System.out.print(res);
}
private static int dfs(char[][] g, int x, int y) {
int n = g.length;
int m = g[0].length;
if (x < 0 || y < 0 || x >= n || y >= m || g[x][y] == '*') {
return 0;
}
g[x][y] = '*';
return 1 + dfs(g, x - 1, y) + dfs(g, x, y + 1) + dfs(g, x + 1, y) + dfs(g, x, y - 1);
}
}HJ159 没挡住洪水
描述:
吴铭市近日洪水肆虐,然而市政部门紧急在若干方格上砌起围墙是豆腐渣工程,被洪水中的强腐蚀性物质一氧化二氢分解了,只剩下了用`#`表示的空地。
地图用大小为N×N的字符矩阵描述:`'.'`表示已经被洪水淹没的区域,`'#'`表示空地。四联通的`'#'`组成一个区域。
聪明睿智的吴铭市防洪抗灾紧急委员会官员在全市防洪抗灾紧急会议上指出,在接下来的一天中,洪水仍将上涨,所有与已经被洪水淹没的区域相邻(上下左右方向)的空地格子都会被淹没。请计算在此次上涨后,吴铭市中将有多少个区域被完全淹没。输入描述:
第一行输入整数N(1≦N≦1000)。
随后N行,每行N个字符构成吴铭市的地图,只含`'.'`与`'#'`。已知边界四条边全部为已经被洪水淹没的区域。输出描述:
输出一个整数,表示一天后会完全消失的空地区域数量。
解题思路:
实际是深度优先遍历(DFS),遍历的时候碰到#,对其进行四方向检查,如果四方向都是#,则代表不会被淹没,然后进行DFS,最后获得空地数量
import java.util.*;
public class Main {
private static int[][] dxy = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
private static boolean all;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
char[][] g = new char[n][n];
char[][] copy = new char[n][n];
for (int i = 0; i < n; i++) {
g[i] = in.next().toCharArray();
copy[i] = g[i].clone();
}
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (g[i][j] == '#') {
all = true;
dfs(g, i, j, copy);
if (all) {
res++;
}
}
}
}
System.out.println(res);
}
private static void dfs(char[][] g, int x, int y, char[][] copy) {
int n = g.length;
if (x < 0 || y < 0 || x >= n || y >= n || g[x][y] == '.') {
return;
}
boolean link = false;
// 检查初始区域是否和.相邻
for (int[] d : dxy) {
int i = x + d[0], j = y + d[1];
if (i >= 0 && i < n && j >= 0 && j < n && copy[i][j] == '.') {
link = true;
break;
}
}
// 一旦有一个#不和.相邻, 就不是完全淹没
if (all) {
all = link;
}
g[x][y] = '.';
dfs(g, x - 1, y, copy);
dfs(g, x, y + 1, copy);
dfs(g, x + 1, y, copy);
dfs(g, x, y - 1, copy);
}
}HJ167 清楚姐姐买竹鼠
描述:
清楚姐姐途经山村,遇到一家售卖竹鼠的商铺:
- 花费a元可购买1只竹鼠;
- 花费b元可购买3只竹鼠。
给定a,b,x,求买到至少x只竹鼠所需的最小花费。
输入描述:
在一行上输入三个整数a,b,x(1≦a,b,x≦10⁹)。
输出描述:
输出一个整数,表示最少需花费的金额。
解题思路:
如果买3只没有1只便宜,只按1只买,否则先按3只买,如果有剩余部分,比较买3只和单独买,谁便宜
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
long a = in.nextLong();
long b = in.nextLong();
long x = in.nextLong();
if (b > 3 * a) {
System.out.println(x * a);
} else {
long d = x / 3;
long e = x % 3;
long result = d * b + Math.min(e * a, b);
System.out.println(result);
}
}
}HJ168 小红的字符串
描述:
小红拥有一个长度为n的小写字母字符串s。她可以重复执行如下操作任意次:
选择一个下标i(1≦i≦n),将字符si循环右移到字母表中的下一个字母。特别地,``z``右移后变成``a``。
请计算,使s变为回文串所需的最少操作次数。
【名词解释】回文串:一个字符串从左往右与从右往左读完全相同。输入描述:
一行输入一个长度不超过1000的小写字母字符串s。
输出描述:
在一行上输出一个整数,代表把s变成回文串的最少操作次数。
解题思路:
字符串转字符数组,从两头向中间,比较轴对称两字符的差距,选一个变动小的进行调整
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] ca = in.next().toCharArray();
int count = 0;
if (ca.length % 2 == 0) {
for (int i = 0; i < ca.length / 2; i++) {
int cap1 = 0;
int cap2 = 0;
if (ca[i] > ca[ca.length - 1 - i]) {
cap1 = ca[i] - ca[ca.length - 1 - i];
cap2 = ca[ca.length - 1 - i] + 26 - ca[i];
} else if (ca[i] < ca[ca.length - 1 - i]) {
cap1 = ca[ca.length - 1 - i] - ca[i];
cap2 = ca[i] + 26 - ca[ca.length - 1 - i];
}
count += Math.min(cap1, cap2);
}
} else {
for (int i = 0; i < ca.length / 2 - 1; i++) {
int cap1 = 0;
int cap2 = 0;
if (ca[i] != ca[ca.length - 1 - i]) {
cap1 = ca[i] - ca[ca.length - 1 - i];
cap2 = ca[i] + 26 - ca[ca.length - 1 - i];
}
count += Math.min(cap1, cap2);
}
}
System.out.println(count);
}
}HJ169 灵异背包?
描述:
给定n个正整数{a₁,a₂,…,aₙ},你可以任选若干个放入“灵异背包”。
要求背包内所有数之和为偶数,且在满足偶数的前提下尽可能大。若一个数也不选,则背包和为0。
请输出可以获得的最大偶数和。输入描述:
第一行输入一个整数 n(1≦n≦10⁵)。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦2×10⁴)。输出描述:
输出一个整数,表示满足条件的最大偶数和。
解题思路:
如果相加之和为偶数,直接输出,否则减掉最小的奇数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int[] ia = new int[a];
int minOdd = Integer.MAX_VALUE;
int total = 0;
for (int i = 0; i < a; i++) {
ia[i] = in.nextInt();
total += ia[i];
if (ia[i] % 2 == 1 && ia[i] < minOdd) {
minOdd = ia[i];
}
}
if (total % 2 == 0) {
System.out.println(total);
} else {
System.out.println(total - minOdd);
}
}
}HJ170 01序列
描述:
给定一个数组metrix,数组中只包含1和0,且数组中的1都不相邻,输入一个数n,问能否在将数组中n个0替代换成1后不破坏1都不相邻的条件。
例1 metrix=[1,0,0,0,1],n=1输出true
例2 metrix=[1,0,0,0,1],n=2输出false输入描述:
输入一个数m(1≤m≤100000)表示metrix的长度
第二行m个数0或1表示改位置数组中的元素是0还是1
第三行输入一个数n输出描述:
输出true或false
解题思路:
计算出现的0的个数,如果大于插入数的2倍,则可以
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int[] ia = new int[a];
int total0 = 0;
for (int i = 0; i < a; i++) {
ia[i] = in.nextInt();
if (0 == ia[i]) {
total0++;
}
}
int b = in.nextInt();
if (total0 > 2 * b) {
System.out.println(true);
} else {
System.out.println(false);
}
}
}HJ171 排座椅
描述:
教室内共有n行m列座位,坐在第i行第j列同学的位置记为(i,j)。
为了方便进出,班主任计划设置k条横向通道(贯穿整列的水平通道)与l条纵向通道(贯穿整行的竖直通道)。通道位于相邻两行(或两列)之间。
班主任记录了d对经常交头接耳的同学,他们的位置(xi,yi)与(pi,qi)保证相邻(上下或左右)。她希望通过合理放置通道,使尽可能多的"交头接耳"对被通道隔开。
现请你输出唯一的最优方案,在该方案下,仍未被通道隔开的"交头接耳"对的数量最少。输入描述:
第一行输入五个整数n,m,k,l,d(2≦n,m≦10³;0<k<n;0<l<m;0<d≦2×min{n×m,2×10³})。
接下来d行,每行输入四个整数xᵢ,yᵢ,pᵢ,qᵢ,表示坐标(xᵢ,yᵢ)与(pᵢ,qᵢ)的两位同学会交头接耳,且两坐标上下相邻或左右相邻。
保证最优方案存在且唯一。输出描述:
第一行输出k个严格递增的整数a₁,a₂,…,aₖ(1≦a₁<⋯<aₖ≦n−1),在行aᵢ与aᵢ+1之间设置横向通道。
第二行输出l个严格递增的整数b₁,b₂,…,bₗ(1≦b₁<⋯<bₗ≦m−1),在列bᵢ与bᵢ+1之间设置纵向通道。
解题思路:
贪心算法,先算行之间分隔最多的,再算列之间分隔最多的
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int k = scanner.nextInt();
int l = scanner.nextInt();
int d = scanner.nextInt();
// 行分隔线,索引表示在第i行和第i+1行之间
int[] rowCount = new int[n];
// 列分隔线,索引表示在第j列和第j+1列之间
int[] colCount = new int[m];
for (int i = 0; i < d; i++) {
int x1 = scanner.nextInt();
int y1 = scanner.nextInt();
int x2 = scanner.nextInt();
int y2 = scanner.nextInt();
if (x1 == x2) {
// 同一行,上下相邻,需要在列之间设置分隔
int col = Math.min(y1, y2);
colCount[col]++;
} else {
// 同一列,左右相邻,需要在行之间设置分隔
int row = Math.min(x1, x2);
rowCount[row]++;
}
}
List<int[]> rowList = new ArrayList<>();
for (int i = 1; i < n; i++) {
if (rowCount[i] > 0) {
rowList.add(new int[]{i, rowCount[i]});
}
}
rowList.sort((a, b) -> {
if (a[1] != b[1]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
int[] rowResult = new int[k];
for (int i = 0; i < k && i < rowList.size(); i++) {
rowResult[i] = rowList.get(i)[0];
}
Arrays.sort(rowResult);
for (int i = 0; i < k; i++) {
System.out.print(rowResult[i] + (i == k - 1 ? "\n" : " "));
}
List<int[]> colList = new ArrayList<>();
for (int i = 1; i < m; i++) {
if (colCount[i] > 0) {
colList.add(new int[]{i, colCount[i]});
}
}
colList.sort((a, b) -> {
if (a[1] != b[1]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
int[] colResult = new int[l];
for (int i = 0; i < l && i < colList.size(); i++) {
colResult[i] = colList.get(i)[0];
}
Arrays.sort(colResult);
for (int i = 0; i < l; i++) {
System.out.print(colResult[i] + (i == l - 1 ? "\n" : " "));
}
}
}HJ172 小红的矩阵染色
描述:
给定一个n×m的矩阵,初始时部分格子已被染成黑色(用``*``表示),其余格子为空白(用 ``o``表示)。
小红最多可以任选至多k个空白格子,将其染成红色。计分规则如下:
- 若某个红色格子的正下方(同一列下一行)也是红色,则该格子贡献1分;
- 其他情况不计分。
请你帮小红计算,经过最优染色后,最多能获得多少分数。
输入描述:
第一行输入三个整数n,m,k(1≦n,m≦10³;1≦k≦n×m),分别表示矩阵行数、列数及最多可染红的格子数量。
此后n行,每行输入一个长度为m的字符串sᵢ,描述第i行初始状态:
- ``*``代表黑色格子,不能重新染色;
- ``o``代表空白格子,可选择染为红色。
输出描述:
输出一个整数,表示小红通过最佳策略能够获得的最大分数。
解题思路:
按列遍历,找出所有垂直连续的白色块(长度≥2),然后倒序排序,先染最长的,然后依次染色,计算分数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 矩阵行数
int n = sc.nextInt();
// 矩阵列数
int m = sc.nextInt();
// 最多可染色的格子数
int k = sc.nextInt();
char[][] matrix = new char[n][m];
// 读取矩阵数据
for (int i = 0; i < n; i++) {
matrix[i] = sc.next().toCharArray();
}
List<Integer> blockLengths = new ArrayList<>();
// 按列遍历,找出所有垂直连续的白色块(长度≥2)
// 遍历每一列
for (int j = 0; j < m; j++) {
// 当前连续白色块的长度
int currentBlockLength = 0;
// 遍历列中的每一行
for (int i = 0; i < n; i++) {
// 遇到白色格子,增加块长度
if (matrix[i][j] == 'o') {
currentBlockLength++;
} else { // 遇到非白色格子(黑色)
// 若当前块长度≥2,记录下来(只有≥2的块才能产生得分)
if (currentBlockLength >= 2) {
blockLengths.add(currentBlockLength);
}
// 重置块长度
currentBlockLength = 0;
}
}
// 处理列末尾可能存在的连续白色块
if (currentBlockLength >= 2) {
blockLengths.add(currentBlockLength);
}
}
// 按块长度从大到小排序(优先处理长块,能产生更多得分)
Collections.sort(blockLengths, Collections.reverseOrder());
int score = 0;
// 遍历所有块,计算最大得分
for (int length : blockLengths) {
// 染色次数用尽,退出
if (k == 0) {
break;
}
// 取当前块长度与剩余染色次数的较小值(最多染这么多格子)
int cellsToDye = Math.min(k, length);
// 只有染色数≥2时才能产生得分(连续2个格子产生1分,3个产生2分,以此类推)
if (cellsToDye >= 2) {
score += cellsToDye - 1;
}
// 消耗染色次数
k -= cellsToDye;
}
System.out.println(score);
}
}HJ173 小红的魔法药剂
描述:
小红打算收集编号为1∼n的n种魔法药剂,其中每种药剂有两种形态:红色版本与蓝色版本。
获得药剂的方式如下:
- 直接购买:购买一瓶第i种红色版本药剂需要花费ai金币;
- 调配合成:若已拥有红色版本的第bi种与第ci种药剂,可分别消耗一瓶,调配得到蓝色版本的第i种药剂,调配本身不额外花费金币(仅需保证两种原料存在)。
小红不关心颜色,只要求最终至少拥有1∼n每种药剂中的任意一种形态(红或蓝)。请计算她所需支付的最小总金币数。
输入描述:
第一行输入一个整数n(1≦n≦10⁵),表示药剂种类数量。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁴),依次表示直接购买一瓶第i种红色药剂的价格。
接下来n行,第i行输入两个整数bᵢ,cᵢ(1≦bᵢ,cᵢ≦n),表示合成蓝色版本第i种药剂所需的两种红色药剂的编号。输出描述:
输出一个整数,表示获得n种不同药剂所需支付的最小金币数。
解题思路:
比较合成和直接购买的价格,然后选最便宜的累加
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int a = in.nextInt();
int[] aa = new int[a];
for (int i = 0 ; i < a ; i ++) {
aa[i] = in.nextInt();
}
int total = 0;
for (int i = 0 ; i < a ; i ++) {
int i1 = in.nextInt();
int i2 = in.nextInt();
int temp = aa[i1 - 1] + aa[i2 - 1];
total += Math.min(temp, aa[i]);
}
System.out.println(total);
}
}HJ174 交换到最大
描述:
给定一个仅由数字0-9构成的字符串s。一次操作可按如下方式进行:
- 从s中选择既不是最左端字符也不为0的某一字符;
- 将该字符的数值减少1;
- 随后把它与左侧相邻字符交换位置。
例如,字符串"1023"经过一次操作可以变成"1103"或"1022"。
你可以不限次数地执行上述操作。请计算能够得到的字典序最大的字符串,并输出该字符串。输入描述:
第一行输入一个整数t(1≦t≦10⁴),表示测试用例数量。
此后t行,每行输入一个不含前导零的数字字符串s,满足1≦∣s∣≦2×10⁵。
保证所有测试用例的∣s∣之和不超过2×10⁵。输出描述:
对于每个测试用例,在一行上输出通过任意次数操作后能够得到的字典序最大的字符串。
解题思路:
相邻两数满足差值≥2时,交换并减1
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int line = in.nextInt();
in.nextLine();
for (int count = 0; count < line; count++) {
char[] chars = in.nextLine().toCharArray();
int[] s = new int[chars.length];
for (int i = 0; i < chars.length; i++) {
s[i] = Character.getNumericValue(chars[i]);
}
boolean flag = true;
// 循环执行操作直到无法继续
while (flag) {
flag = false;
// 从右向左执行
for (int i = s.length - 1; i > 0; i--) {
// 满足差值≥2时交换并减1
if (s[i] - s[i - 1] >= 2) {
int tmp = s[i];
s[i] = s[i - 1];
s[i - 1] = tmp - 1;
}
}
// 检查是否还能操作
for (int i = s.length - 1; i > 0; i--) {
if (s[i] - s[i - 1] >= 2) {
flag = true;
break;
}
}
}
// 输出结果
for (int i : s) {
System.out.print(i);
}
System.out.println();
}
}
}HJ175 小红的整数配对
描述:
小红拥有一个长度为n的整数数组{a₁,a₂,…,aₙ},初始得分为0。
她可以多次执行如下操作,顺序不限、次数不限,直到无法继续:
- 任选两个尚未被选过的下标 i≠j;
- 若满足∣aᵢ−aⱼ∣≦k,则将这两个数配成一对,并获得分数aᵢ×aⱼ;否则该对无法选取;
- 被配对的两个数随即从数组中移除,之后不可再次使用。
请你帮助小红最大化最终得分,并输出这个最大分数。
输入描述:
在一行上输入两个整数n,k(1≦n,k≦10⁵)。
在第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁵)。输出描述:
输出一个整数,表示通过最优配对操作后小红能够获得的最大得分。
解题思路:
对元素排序后遍历,比较相邻两元素,是否符合差值,符合后相乘累加,直到遍历结束
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
int cap = in.nextInt();
long[] ia = new long[count];
for (int i = 0; i < count; i++) {
ia[i] = in.nextInt();
}
Arrays.sort(ia);
long result = 0;
for (int i = count - 1; i >= 1; i--) {
if (ia[i] - ia[i - 1] <= cap) {
result += ia[i] * ia[i - 1];
i--;
}
}
System.out.println(result);
}
}HJ177 可匹配子段计数
描述:
给定整数数组a(长度n)与数组b(长度m,m≦n)。设一个长度为m的数组c被称为可匹配的,当且仅当将c的元素重新排列后,与数组b在对应位置上至少有k个元素相等。
对于a中的每一个长度恰为m的连续子段,都可视为一个候选数组c。求满足条件的子段数量。
【形式化解释】
若子段经重排可与b至少k个位置相等,则称该子段为"可匹配的"。等价地,设cntₓ(S)为元素x在序列S中出现次数,则子段c的"匹配度"为
,若 match(c)≧k则符合要求。
输入描述:
第一行输入整数t(1≦t≦10⁴)——测试用例组数。
每个测试用例:
- 一行三个整数n,m,k(1≦k≦m≦n≦2×10⁵);
- 一行n个整数a₁…aₙ(1≦a₁≦10⁶);
- 一行m个整数b₁…bₘ(1≦b₁≦10⁶)。
输入保证所有测试用例的n之和、m之和均不超过2×10⁵。
输出描述:
对每个测试用例输出一行整数,表示满足条件的子段数量。
解题思路:
计算b数组,字符出现的频率,然后对a数组计算字符出现的频率,计算重叠的字符的数量是否达到阈值,然后滑动,对重叠数量进行增减,对窗口元素频率进行增减,然后匹配阈值,最后计算符合阈值的数量
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
while (n-- > 0) {
solve(in);
}
}
public static void solve(Scanner sc) {
int n = sc.nextInt();
int m = sc.nextInt();
int k = sc.nextInt();
int[] a = new int[n];
int[] b = new int[m];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = 0; i < m; i++) {
b[i] = sc.nextInt();
}
// 计算b数组字符出现的频率
HashMap<Integer, Integer> bMap = new HashMap<>();
for (int i = 0; i < m; i++) {
bMap.put(b[i], bMap.getOrDefault(b[i], 0) + 1);
}
// 初始化第一个窗口,计算初始重叠元素数量
HashMap<Integer, Integer> aMap = new HashMap<>();
for (int i = 0; i < m; i++) {
aMap.put(a[i], aMap.getOrDefault(a[i], 0) + 1);
}
// 最终结果
int result = 0;
// 重叠数量
int count = 0;
//计算第一个窗口的重叠数量
for (Integer key : bMap.keySet()) {
count += Math.min(aMap.getOrDefault(key, 0), bMap.get(key));
}
// 重叠数量如果超过阈值,增加结果
if (count >= k) {
result++;
}
// 滑动窗口
for (int i = m; i < n; i++) {
// 移除的元素
int remove = a[i - m];
// 新增的元素
int add = a[i];
// 处理从窗口移除的元素
if (bMap.containsKey(remove)) {
if (aMap.getOrDefault(remove, 0) <= bMap.get(remove)) {
count--;
}
}
aMap.put(remove, aMap.get(remove) - 1);
if (aMap.get(remove) == 0) {
aMap.remove(remove);
}
// 处理加入窗口的元素
if (bMap.containsKey(add)) {
if (aMap.getOrDefault(add, 0) < bMap.get(add)) {
count++;
}
}
aMap.put(add, aMap.getOrDefault(add, 0) + 1);
// 重叠数量如果超过阈值,增加结果
if (count >= k) {
result++;
}
}
System.out.println(result);
}
}中等难度
HJ16 购物单
描述:
王强决定把年终奖用于购物,他把想买的物品分为两类:主件与附件。
- 主件可以没有附件,至多有2个附件。附件不再有从属于自己的附件。
- 若要购买某附件,必须先购买该附件所属的主件,且每件物品只能购买一次。
王强查到了m件物品的价格,而他只有n元的预算。为了先购买重要的物品,他给每件物品规定了一个重要度,用整数1∼5表示。他希望在不超过预算的前提下,使满意度最大。
满意度定义为所购每件物品价格与重要度乘积之和。具体地说,记第i件物品的价格为vᵢ,重要度wi;若共选中k件物品,编号为j₁,j₂,…,jₖ,则满意度计算为:
请你帮助王强计算可获得的最大的满意度。
输入描述:
第一行输入两个整数n,m(1≦n≦3×10⁴; 1≦m≦60)代表预算、查询到的物品总数。
此后m行,第i行输入三个整数vᵢ,wᵢ,qᵢ(1≦vᵢ≦10⁴; 1≦wᵢ≦5; 0≦qᵢ≦m)代表第i件物品的价格、重要度、主件编号。特别地,qᵢ=0代表该物品为主件,否则表示该附件从属于主件qᵢ。编号即输入顺序,从1开始。
特别地,保证全部物品的价格v均为10的倍数;且每个主件的附件数不超过2个。输出描述:
在一行上输出一个整数,代表王强可获得的最大满意度。
解题思路:
带附件的01背包问题。
01背包问题即有一个容量为V的背包,还有n个物体。现在忽略物体实际几何形状,我们认为只要背包的剩余容量大于等于物体体积,那就可以装进背包里。每个物体都有两个属性,即体积w和价值v。问:如何向背包装物体才能使背包中物体的总价值最大?
其核心算法,是计算dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][j - v] + w)
int[][] dp = new int[m + 1][n + 1],其意思是总共有m件商品,其价值总和为n,第一行和第一列都是0,方便计算,不参与算法
dp[i-1][j],意思是不把物品放入背包,dp[i - 1][j - v] + w,意思是把物品放入背包,不放入,则该元素和上一行元素值相同,dp[i][j] = dp[i-1][j],放入,则则该元素值,为上一行,减去v,即占用的体积,所在元素的值,同时加上该元素的价值,比较谁更大。
该问题带附件,需要多次计算,但是本质相同
import java.util.*;
public class Main {
public static void main(String[] argoods) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
if (m <= 0 || n <= 0) {
System.out.println(0);
}
Good[] goods = new Good[m + 1];
for (int i = 1; i <= m; i++) {
goods[i] = new Good(0, 0, 0);
}
for (int i = 1; i <= m; i++) {
goods[i].v = in.nextInt();
goods[i].w = in.nextInt();
goods[i].q = in.nextInt();
if (goods[i].q > 0) {
if (goods[goods[i].q].ap1 == 0) {
goods[goods[i].q].ap1 = i;
} else {
goods[goods[i].q].ap2 = i;
}
}
}
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
// 只有主件时候的价格
int v = goods[i].v;
// 只有主件时候的重要度
int tempDp = goods[i].w * v;
// 主件+附件1的价格
int v1 = 0;
// 主件+附件2的价格
int v2 = 0;
// 主件+附件1+附件2的价格
int v3 = 0;
// 主件+附件1的重要度
int tempDp1 = 0;
// 主件+附件2的重要度
int tempDp2 = 0;
// 主件+附件1+附件2的重要度
int tempDp3 = 0;
// 附件1存在时
if (goods[i].ap1 != 0) {
v1 = goods[goods[i].ap1].v + v;
tempDp1 = tempDp + goods[goods[i].ap1].v * goods[goods[i].ap1].w;
}
// 附件2存在时
if (goods[i].ap2 != 0) {
v2 = goods[goods[i].ap2].v + v;
tempDp2 = tempDp + goods[goods[i].ap2].v * goods[goods[i].ap2].w;
}
// 附件1和附件2都存在时
if (goods[i].ap1 != 0 && goods[i].ap2 != 0) {
v3 = goods[goods[i].ap1].v + goods[goods[i].ap2].v + v;
tempDp3 = tempDp + goods[goods[i].ap1].v * goods[goods[i].ap1].w + goods[goods[i].ap2].v * goods[goods[i].ap2].w;
}
for (int j = 1; j <= n; j++) {
// 当物品i是附件时,相当于跳过
if (goods[i].q > 0) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j];
if (j >= v && v != 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v] + tempDp);
}
if (j >= v1 && v1 != 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v1] + tempDp1);
}
if (j >= v2 && v2 != 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v2] + tempDp2);
}
if (j >= v3 && v3 != 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v3] + tempDp3);
}
}
}
}
System.out.println(dp[m][n]);
}
/**
* 定义物品类
*/
private static class Good {
// 价格
public int v;
// 重要度
public int w;
// 主附件ID
public int q;
// 附件1 ID
public int ap1 = 0;
// 附件2 ID
public int ap2 = 0;
public Good(int v, int w, int q) {
this.v = v;
this.w = w;
this.q = q;
}
}
}HJ17 坐标移动
描述:
我们定义一个无限大的二维网格上有一个小人,小人初始位置为(0,0)点,小人可以读取指令上下左右移动。一个合法的指令由三至四个符号组成:
- 第一个符号为"A/D/W/S"中的一个,代表小人移动的方向;分别代表向左、向右、向上、向下移动;记某个时刻小人的坐标为(x,y),向左移动一格即抵达(x−1,y)、向右移动一格即抵达(x+1,y)、向上移动一格即抵达(x,y+1)、向下移动一格即抵达(x,y−1)。
- 最后一个符号为‘;’,代表指令的结束,该符号固定存在;
- 中间为一个大于0且小于100的数字,代表小人移动的距离。特别地,如果这个数字小于10,那么它可能包含一个前导零,此时也视为合法。
如果你遇到了一个不合法的指令,则直接忽略;例如,指令"A100;"是不合法的,因为100超出了规定的数字范围;"Y10;"也是不合法的,因为Y不是"A/D/W/S"中的一个。
输出小人最终的坐标。输入描述:
在一行上输入一个长度1≦length(s)≦10⁴,由大写字母、数字和分号(‘;’)构成的字符串s,代表输入的指令序列。保证字符串中至少存在一个‘;’,且末尾一定为‘;’。
输出描述:
在一行上输出一个两个整数,代表小人最终位置的横纵坐标,使用逗号间隔。
解题思路:
String.split(String regex),按;拆分字符串,循环字符串数组,看是否匹配[A][1-9][0-9]{0,1},[D][1-9][0-9]{0,1},[W][1-9][0-9]{0,1},[S][1-9][0-9]{0,1},依次处理
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] strings = in.nextLine().split(";");
int x = 0;
int y = 0;
for (int i = 0; i < strings.length; i++) {
if (strings[i].matches("[A][1-9][0-9]{0,1}")) {
x = x - Integer.parseInt(strings[i].substring(1));
} else if (strings[i].matches("[D][1-9][0-9]{0,1}")) {
x = x + Integer.parseInt(strings[i].substring(1));
} else if (strings[i].matches("[W][1-9][0-9]{0,1}")) {
y = y + Integer.parseInt(strings[i].substring(1));
} else if (strings[i].matches("[S][1-9][0-9]{0,1}")) {
y = y - Integer.parseInt(strings[i].substring(1));
}
}
System.out.println(x + "," + y);
}
}HJ20 密码验证合格程序
描述:
你需要书写一个程序验证给定的密码是否合格。
合格的密码要求:
- 长度不少于8位
- 必须包含大写字母、小写字母、数字、特殊字符中的至少三种
- 不能分割出两个独立的、长度大于2的连续子串,使得这两个子串完全相同;更具体地,如果存在两个长度大于2的独立子串s1,s2,使得s1=s2,那么密码不合法。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。
可见字符集为ASCII码在33到126范围内的可见字符。
输入描述:
本题将会给出1≦T≦10组测试数据,确切数字未知,您需要一直读入直到文件结尾;每组测试数据描述如下:
在一行上输入一个长度为1≦length(s)≦100,由可见字符构成的字符串s,代表待判断的密码。输出描述:
对于每一组测试数据,新起一行。若密码合格,输出OK,否则输出NG。
解题思路:
String.length(),计算长度,Pattern.compile(String regex),匹配大写[A-Z],小写[a-z],数字[0-9],特殊字符[^a-zA-Z0-9],计算得分,getString方法校验是否有重复子串
import java.util.*;
import java.util.regex.*;
public class Main {
public static void main(String[] arg) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
String str = sc.next();
if (str.length() <= 8) {
System.out.println("NG");
continue;
}
if (getMatch(str)) {
System.out.println("NG");
continue;
}
if (getString(str, 0, 3)) {
System.out.println("NG");
continue;
}
System.out.println("OK");
}
}
// 校验是否有重复子串
private static boolean getString(String str, int l, int r) {
if (r >= str.length()) {
return false;
}
if (str.substring(r).contains(str.substring(l, r))) {
return true;
} else {
return getString(str, l + 1, r + 1);
}
}
// 检查是否满足正则
private static boolean getMatch(String str) {
int count = 0;
Pattern p1 = Pattern.compile("[A-Z]");
if (p1.matcher(str).find()) {
count++;
}
Pattern p2 = Pattern.compile("[a-z]");
if (p2.matcher(str).find()) {
count++;
}
Pattern p3 = Pattern.compile("[0-9]");
if (p3.matcher(str).find()) {
count++;
}
Pattern p4 = Pattern.compile("[^a-zA-Z0-9]");
if (p4.matcher(str).find()) {
count++;
}
if (count >= 3) {
return false;
} else {
return true;
}
}
}HJ24 合唱队
描述:
音乐课上,老师将n位同学排成一排。老师希望在不改变同学相对位置的前提下,从队伍中选出最少数量的同学,使得剩下的同学排成合唱队形。
记合唱队形中一共有k位同学,记编号为1,2,…,k,第i个人的身高为hᵢ。要求:存在一位同学编号为i(1<i<k),使得严格递增,且
严格递减;更具体地,合唱队形呈
。
你能帮助老师计算,最少需要出列多少位同学,才能使得剩下的同学排成合唱队形?输入描述:
第一行输入一个整数n(1≦n≦3000)代表同学数量。
第二行输入n个整数h₁,h₂,…,hₙ(0≦hᵢ≦10⁵)代表每一位同学的身高。输出描述:
输出一个整数,代表最少需要出列的同学数量。
解题思路:
使用动态规划法,获取最长递增子序列,设置一个和原数组等长的全1数组,因为每个元素自身就占1个长度,核心算法为
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}即遍历数组的时候,有index为i,j,且i > j,如果后面的数字num[i],大于前面的数字num[j],则递增子序列的长度,至少为dp[j] + 1,则需要和原来已有的dp[i],比较谁大,更新长度数组。
该题目,从前往后遍历一遍,再从后往前遍历一遍,得到两个最长递增子序列,然后再减掉重复的1个,遍历长度数组,max = Math.max(dp1[i] + dp2[i] - 1, max),max就是最后人数,
n - max就是答案。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = in.nextInt();
}
int[] dp1 = new int[n];
int[] dp2 = new int[n];
Arrays.fill(dp1, 1);
Arrays.fill(dp2, 1);
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp1[i] = Math.max(dp1[i], dp1[j] + 1);
}
}
}
for (int i = n - 2; i >= 0; i--) {
for (int j = n - 1; j > i; j--) {
if (nums[i] > nums[j]) {
dp2[i] = Math.max(dp2[i], dp2[j] + 1);
}
}
}
int max = 0;
for (int i = 0; i < n; i++) {
max = Math.max(dp1[i] + dp2[i] - 1, max);
}
System.out.println(n - max);
}
}HJ26 字符串排序
描述:
对于给定的由可见字符和空格组成的字符串,按照下方的规则进行排序:
- 按照字母表中的顺序排序(不区分大小写);
- 同一字母的大小写同时存在时,按照输入顺序排列;
- 非字母字符保持原来的位置不参与排序;
- 直接输出排序后的字符串。
字符串由 ASCII 码在32到126范围内的字符组成。您可以参阅下表获得其详细信息。
输入描述:
在一行上输入一个长度为1≦length(s)≦1000,由上表中的字符组成的字符串s 。
输出描述:
输出一个字符串,代表按照规则排序后的字符串。
解题思路:
String[] strings = new String[26],字符串转为字符数组,对字符数组遍历,碰到相应的大小写,拼接到字符串数组,char[] noAlphats = new char[chars.length],碰到相应的数字,放到对应位置,然后将strings数组拼接为字符串,遍历noAlphats数组,碰到非'\u0000',在字符相应位置插入数字字符。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.nextLine().toCharArray();
String[] strings = new String[26];
for (int i = 0; i < 26; i++) {
strings[i] = "";
}
char[] noAlphats = new char[chars.length];
for (int i = 0; i < chars.length; i++) {
if (chars[i] >= 'a' && chars[i] <= 'z') {
strings[chars[i] - 'a'] += chars[i];
} else if (chars[i] >= 'A' && chars[i] <= 'Z') {
strings[chars[i] - 'A'] += chars[i];
} else {
noAlphats[i] = chars[i];
}
}
StringBuffer sb = new StringBuffer();
for (int i = 0; i < strings.length; i++) {
if (strings[i] != null) {
sb.append(strings[i]);
}
}
for (int i = 0; i < noAlphats.length; i++) {
if (noAlphats[i] != '\u0000') {
sb.insert(i, noAlphats[i]);
}
}
System.out.println(sb);
}
}HJ27 查找兄弟单词
描述:
定义一个字符串s的“兄弟单词”为:将s重新排序后得到的与原字符串不同的新字符串。
现在,对于给定的n个字符串s₁,s₂,…,sₙ和另一个单独的字符串x,你需要解决两个问题:
- 统计这n个字符串中,有多少个是x的“兄弟单词”(注意,这n个字符串可能有重复,重复字符串分别计数);
- 将这n个字符串中x的“兄弟单词”按字典序从小到大排序,输出排序后的第k个兄弟单词(从1开始计数)。特别地,如果不存在,则不输出任何内容。
【名词解释】
从字符串的第一个字符开始逐个比较,直至发现第一个不同的位置,比较这个位置字符的字母表顺序,字母序较小的字符串字典序也较小;如果比较到其中一个字符串的结尾时依旧全部相同,则较短的字符串字典序更小。输入描述:
在一行上依次输入:
- 一个整数n(1≦n≦10³)代表字符串的个数;
- n个长度为1≦length(sᵢ)≦10,仅由小写字母构成的字符串s₁,s₂,…,sₙ;
- 一个长度为1≦length(x)≦10,仅由小写字母构成的字符串x;
- 一个整数k(1≦k≦n)代表要查找的第k小的兄弟单词的序号。
输出描述:
第一行输出一个整数,代表给定的n个字符串中,x的“兄弟单词”的数量;
第二行输出一个字符串,代表将给定的n个字符串中x的“兄弟单词”按字典序排序后的第k小兄弟单词。特别地,如果不存在,则不输出任何内容(完全省略第二行)。
解题思路:
Set<Character> 获取需要匹配的字符串的不同字符,如果Set中元素的数量小于2,则一定没有兄弟单词,然后将相应的字符串,变为字符数组,排序后,重新生成字符串,要求重新生成的字符串相同,但原字符串不同,否则就不是兄弟单词,符合条件的单词,放入List<String>,然后判断k是否大于List中元素的数量,如果合适输出。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
String[] arr = new String[n];
for (int i = 0; i < n; i++) {
arr[i] = in.next();
}
String x = in.next();
Set<Character> set = new HashSet<>();
char[] xCharArray = x.toCharArray();
for (int i = 0; i < xCharArray.length; i++) {
set.add(xCharArray[i]);
}
if (set.size() <= 1) {
System.out.println(0);
return;
}
Arrays.sort(xCharArray);
String xa = String.valueOf(xCharArray);
int k = in.nextInt();
List<String> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
char[] charArray = arr[i].toCharArray();
Arrays.sort(charArray);
String temp = String.valueOf(charArray);
if (temp.equals(xa) && !x.equals(arr[i])) {
list.add(arr[i]);
}
}
list.sort(null);
System.out.println(list.size());
if (list.size() >= k) {
System.out.println(list.get(k - 1));
}
}
}HJ29 字符串加解密
描述:
规定这样一种密码的加密方法:
- 对于密码中的英文字母,按照字母表顺序,向后移动一位,同时改变大小写,即Z转换为a,A转换为b,B转换为c,⋯⋯ ,Y转换为z,Z转换为a。
- 对于密码中的数字,增加1,9转换为0。
字符串的解密方法即为加密方法的逆过程。
现在,对于给定的明文字符串s,将其加密;对于给定的密文字符串t,将其解密。输入描述:
第一行输入一个长度为1≦length(s)≦10³的字符串s,代表给定的明文字符串;
第二行输入一个长度为1≦length(t)≦10³的字符串t ,代表给定的密文字符串。
除此之外,保证字符串s和t中仅包含英文字母和数字。输出描述:
第一行输出一个字符串,代表加密后的s。
第二行输出一个字符串,代表解密后的t。
解题思路:
按相应的条件,逆序处理
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars1 = in.nextLine().toCharArray();
char[] chars2 = in.nextLine().toCharArray();
for (int i = 0; i < chars1.length; i++) {
if (Character.isLowerCase(chars1[i])) {
if ('z' == chars1[i]) {
chars1[i] = 'A';
} else {
chars1[i] = (char) Character.toUpperCase(chars1[i] + 1);
}
} else if (Character.isUpperCase(chars1[i])) {
if ('Z' == chars1[i]) {
chars1[i] = 'a';
} else {
chars1[i] = (char) Character.toLowerCase(chars1[i] + 1);
}
} else if (Character.isDigit(chars1[i])) {
if ('9' == chars1[i]) {
chars1[i] = '0';
} else {
chars1[i] = (char) (chars1[i] + 1);
}
}
}
System.out.println(String.valueOf(chars1));
for (int i = 0; i < chars2.length; i++) {
if (Character.isLowerCase(chars2[i])) {
if ('a' == chars2[i]) {
chars2[i] = 'Z';
} else {
chars2[i] = (char) Character.toUpperCase(chars2[i] - 1);
}
} else if (Character.isUpperCase(chars2[i])) {
if ('A' == chars2[i]) {
chars2[i] = 'z';
} else {
chars2[i] = (char) Character.toLowerCase(chars2[i] - 1);
}
} else if (Character.isDigit(chars2[i])) {
if ('0' == chars2[i]) {
chars2[i] = '9';
} else {
chars2[i] = (char) (chars2[i] - 1);
}
}
}
System.out.println(String.valueOf(chars2));
}
}HJ32 密码截取
描述:
Catcher是MCA国的情报员,他工作时发现敌国会用一些对称的密码进行通信,比如像这些"ABBA"、"ABA"、"A"、"123321"。
但是他们有时会在开始或结束时加入一些无关的字符以防止别国破解。比如进行下列变化"ABBA"→"12ABBA"、"ABA"→"ABAKK","123321"→"51233214"。因为截获的串太长了,而且存在多种可能的情况("abaaab"可看作是"aba"或 "baaab"的加密形式),Cathcer的工作量实在是太大了,他只能向电脑高手求助,你能帮Catcher找出最长的有效密码串吗?输入描述:
在一行上输入一个长度为1≦length(s)≦2500,仅由大小写字母和数字构成的字符串s,代表截获的密码。
输出描述:
在一行上输出一个整数,代表最长的有效密码串的长度。
解题思路:
本质和HJ85一样,就是求最长回文数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.next();
int max = 0;
for (int i = 0; i < s.length(); i++) {
//奇数长度回文数
int i1 = huiWenShu(s, i, i);
//偶数长度回文数
int i2 = huiWenShu(s, i, i + 1);
//判断最长的回文子串的长度
int i3 = Math.max(i1, i2);
// 如果找到更长的回文,更新
if (i3 > max) {
max = i3;
}
}
System.out.println(max);
}
public static int huiWenShu(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return right - left - 1;
}
}HJ33 整数与IP地址间的转换
描述:
原理:ip地址的每段可以看成是一个0-255的整数,把每段拆分成一个二进制形式组合起来,然后把这个二进制数转变成
一个长整数。
举例:一个ip地址为10.0.3.193
每段数字 相对应的二进制数
10 00001010
0 00000000
3 00000011
193 11000001组合起来即为:00001010 00000000 00000011 11000001,转换为10进制数就是:167773121,即该IP地址转换后的数字就是它了。
数据范围:保证输入的是合法的 IP 序列
输入描述:
输入
1 输入IP地址
2 输入10进制型的IP地址输出描述:
输出
1 输出转换成10进制的IP地址
2 输出转换后的IP地址
解题思路:
String[] nums = string.split("\\."),然后对nums[i]转为Long,依次 <<24, <<16, <<8, <<0(省略),对于long类型的num,依次>> 24,>> 16,>> 8,>> 0(省略),再& 0xff
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String string = in.nextLine();
Long num = in.nextLong();
String[] nums = string.split("\\.");
System.out.println((Long.parseLong(nums[0]) << 24) + (Long.parseLong(nums[1]) << 16) + (Long.parseLong(nums[2]) << 8) + (Long.parseLong(nums[3])));
System.out.println(((num >> 24) & 0xff) + "." + ((num >> 16) & 0xff) + "." + ((num >> 8) & 0xff) + "." + ((num) & 0xff));
}
}HJ36 字符串加密
描述:
对于给定的字符串s,我们可以利用其进行加密。
具体地,首先先将s进行去重,即如果s中存在重复的字母,则只保留第一次出现的字母。随后,从"a"开始依次在字符串末尾补充s中未出现的字母,使得s成为一个完整的字母表。
最后,对于给定的明文t,我们利用上述字母表进行加密,即对于t中的每个字母,替换为s构建得到的新字母表中相同位置的字母。输入描述:
第一行输入一个长度为1≦length(s)≦100,仅由小写字母构成的字符串s,代表待构建的新字母表底串。
第二行输入一个长度为1≦length(t)≦100,仅由小写字母构成的字符串t,代表需要加密的明文。输出描述:
在一行上输出一个字符串,代表加密后的密文。
解题思路:
按题目要求处理加密
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.nextLine().toCharArray();
char[] chars2 = in.nextLine().toCharArray();
int[] alphat = new int[26];
StringBuffer start = new StringBuffer();
Set<Character> set = new LinkedHashSet<>();
for (int i = 0; i < chars.length; i++) {
alphat[chars[i] - 'a']++;
set.add(chars[i]);
}
StringBuffer end = new StringBuffer();
for (Character c : set) {
start.append(c);
}
for (int i = 0; i < alphat.length; i++) {
if (alphat[i] == 0) {
start.append((char) (i + 'a'));
}
}
char[] after = start.append(end).toString().toCharArray();
StringBuffer result = new StringBuffer();
for (int i = 0; i < chars2.length; i++) {
result.append(after[chars2[i] - 'a']);
}
System.out.println(result);
}
}HJ38 求小球落地5次后所经历的路程和第5次反弹的高度
描述:
假设有一个小球从h米高度自由落下,我们不考虑真实的物理模型,而是简洁的假定,该小球每次落地后会反弹回原高度的一半;再落下,再反弹;……。
求小球在第五次落地时所经历的路程和第五次反弹的高度。
在本题中,路程的计算仅需考虑垂直方向的变化。输入描述:
在一行上输入一个整数h(1≦h≦10³)代表小球的初始高度。
输出描述:
第一行输出一个实数,代表小球在第五次落地时所经历的路程。
第二行输出一个实数,代表第五次反弹的高度。
由于实数的计算存在误差,当误差的量级不超过10⁻⁶时,您的答案都将被接受。具体来说,设您的答案为a,标准答案为b,当且仅当∣a−b∣/max(1,∣b∣)≦10⁻⁶时,您的答案将被接受。
解题思路:
参数循环 / 2,一共5次,每次累加,总路程为初始高度 + 累加高度 × 2,第5次高度为最后一次 / 2的高度。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
double origin = in.nextDouble();
double d1 = origin;
double result1 = 0;
for (int i = 0; i < 5; i++) {
d1 /= 2;
result1 += d1;
}
result1 -= d1;
System.out.println(origin + 2 * (result1));
System.out.println(d1);
}
}HJ41 称砝码
描述:
对于给定的n种砝码,重量互不相等,依次为m₁,m₂,…,mₙ,数量依次为x₁,x₂,…,xₙ,
现在要用这些砝码去称物体的重量(放在同一侧),问能称出多少种不同的重量。特别地,称重重量包括0。输入描述:
第一行输入一个整数n(1≦n≦10)代表砝码的个数。
第二行输入n个整数m₁,m₂,…,mₙ(1≦mᵢ≦2000)代表每种砝码的重量。
第三行输入n个整数x₁,x₂,…,xₙ(1≦xᵢ≦10)代表每种砝码的数量。输出描述:
输出一个整数,代表利用给定的砝码可以称出的不同的重量数。
解题思路:
先把各个砝码的重量,都放在weights数组里,然后使用动态规划法,依次获取可能出现的砝码重量,放入Set集合,最后计算Set大小。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
int[] weight = new int[count];
int[] size = new int[count];
for (int i = 0; i < count; i++) {
weight[i] = in.nextInt();
}
int sumCount = 0;
for (int i = 0; i < count; i++) {
size[i] = in.nextInt();
sumCount += size[i];
}
int[] weights = new int[sumCount];
int maxSum = 0;
int p = 0;
for (int i = 0; i < count; i++) {
for (int j = 0; j < size[i]; j++) {
weights[p++] = weight[i];
maxSum += weight[i];
}
}
boolean[] dp = new boolean[maxSum + 1];
dp[0] = true;
HashSet<Integer> set = new HashSet<>();
set.add(0);
for (int num : weights) {
for (int j = maxSum; j >= num; j--) {
if (dp[j - num]) {
dp[j] = true;
set.add(j);
}
}
}
System.out.println(set.size());
}
}HJ43 迷宫问题
描述:
有一个h行w列的网格,我们使用(i,j)表示网格中从上往下数第i行和从左往右数第j列的单元格。每个方格要么是可以通过的空方格‘0’,要么是不可通过的墙方格‘1’,特别的,网格的四周都是墙方格,你可以沿着空方格上下左右随意移动:从(x,y)向上移动一格即抵达(x−1,y)、向下移动一格即抵达(x+1,y)、向左移动一格即抵达(x,y−1)、向右移动一格即抵达(x,y+1)。
现在,你位于迷宫的入口(0,0),想要前往终点(h−1,w−1)。请输出一条从起点到终点的可行路径。
保证起点和终点一定为空方格,你始终可以找到且能唯一找到一条从起点出发到达终点的可行路径。
输入描述:
第一行输入两个整数h,w(1≦h,w≦100)代表迷宫的行数和列数。
此后h行,第i行输入w个整数(0≦aᵢ,ⱼ≦1)代表迷宫的布局。其中,aᵢ,ⱼ=0表示单元格(i,j)是空方格,aᵢ,ⱼ=1表示单元格(i,j)是墙方格。
输出描述:
输出若干行,第i行输出两个整数xᵢ,yᵢ,表示路径的第i步抵达的单元格坐标为(xᵢ,yᵢ)。
你需要保证输出的路径是符合题目要求的,即从起点(0,0) 出发,到达终点(h−1,w−1),且路径上每个单元格都是空方格,行走的单元格都是彼此相邻的。
解题思路:
深度优先遍历迷宫
import java.util.*;
public class Main {
public static int h = 0;
public static int w = 0;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
h = in.nextInt();
w = in.nextInt();
int[][] map = new int[h][w];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
map[i][j] = in.nextInt();
}
}
List<int[]> routeList = new ArrayList<>();
dfs(map, 0, 0, routeList);
routeList.add(new int[]{0, 0});
Collections.reverse(routeList);
for (int[] index : routeList) {
System.out.println("(" + index[0] + "," + index[1] + ")");
}
}
private static int[] dfs(int[][] map, int x, int y, List<int[]> routeList) {
if (x < 0 || x >= h || y < 0 || y >= w || map[x][y] == 1) {
return null;
}
if (x == h - 1 && y == w - 1) {
return new int[]{x, y};
}
map[x][y] = 1;
List<int[]> list = new ArrayList<>();
list.add(dfs(map, x + 1, y, routeList));
list.add(dfs(map, x - 1, y, routeList));
list.add(dfs(map, x, y + 1, routeList));
list.add(dfs(map, x, y - 1, routeList));
for (int[] route : list) {
if (route != null) {
routeList.add(route);
return new int[]{x, y};
}
}
return null;
}
}HJ45 名字的漂亮度
描述:
对于给定由小写字母构成的字符串,定义字符串的“漂亮度”为该字符串中所有字母“漂亮度”的总和。
每一个字母的“漂亮度”将由你来确定,具体规则如下:
- 每一个字母的“漂亮度”为1到26之间的整数;
- 没有两个字母的“漂亮度”相同。
现在,你需要确定每个字母的“漂亮度”,以使得字符串的“漂亮度”最大。
输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦10)代表数据组数,每组测试数据描述如下:
在一行上输入一个长度为1≦len(s)≦10⁴、仅由小写字母构成的字符串s。输出描述:
对于每一组测试数据,输出一个整数,表示字符串的最大“漂亮度”。
解题思路:
int[] score = new int[26],统计26字符出现次数,然后倒序排序,根据排序,累加j * score[j - 1],得出分数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] result = new int[n];
for (int i = 0 ; i < n ; i++) {
int[] score = new int[26];
char[] cs = in.next().toCharArray();
for (int j = 0 ; j < cs.length ; j++) {
score[cs[j] - 'a']++;
}
Arrays.sort(score);
int temp = 0;
for (int j = 26 ; j > 0; j--) {
if (score[j - 1] == 0) {
break;
} else {
temp += j * score[j - 1];
}
}
result[i] = temp;
}
for (int i = 0 ; i < n ; i++) {
System.out.println(result[i]);
}
}
}HJ48 从单向链表中删除指定值的节点
描述:
定义一种单向链表的构造方法如下所示:
- 先输入一个整数n,代表链表中节点的总数;
- 再输入一个整数h,代表头节点的值;
- 此后输入n−1个二元组(a,b),表示在值为b的节点后插入值为a的节点。
除此之外,保证输入的链表中不存在重复的节点值。
现在,对于给定的链表构造方法和一个额外的整数k,你需要先按照上述构造方法构造出链表,随后删除值为k的节点,输出剩余的链表。输入描述:
在一行上:
- 先输入一个整数n(1≦n≦10³)代表链表中节点的总数;
- 随后输入一个整数h(1≦h≦10⁴)代表头节点的值;
- 随后输入n−1个二元组(a,b)(1≦a,b≦10⁴)(a,b);
- 最后输入一个整数k,代表需要删除的节点值。
除此之外,保证每一个b值在输入前已经存在于链表中;每一个a值在输入前均不存在于链表中。节点的值各不相同。
输出描述:
在一行上输出n−1个整数,代表删除指定元素后剩余的链表。
解题思路:
使用ArrayList,实现链表功能,遍历List,List.add(int index, E element),实现指定节点添加,Iterator.remove(),实现元素的删除。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
List<Integer> list = new ArrayList<>();
list.add(in.nextInt());
for (int i = 0; i < n - 1; i++) {
int a = in.nextInt();
int b = in.nextInt();
for (int j = 0; j < list.size(); j++) {
int temp = list.get(j);
if (b == temp) {
list.add(j + 1, a);
break;
}
}
}
int d = in.nextInt();
Iterator<Integer> iterator = list.iterator();
while (iterator.hasNext()) {
int temp = iterator.next();
if (d == temp) {
iterator.remove();
}
}
StringBuffer sb = new StringBuffer();
for (int i : list) {
sb.append(i);
sb.append(" ");
}
System.out.println(sb.toString().trim());
}
}HJ50 四则运算
描述:
对于输入的表达式,保证其形式合法、计算过程中全程合法、计算过程中不需要使用到实数、结果ans满足−10³≦ans≦10³。直接输出计算结果。
保证表达式字符串由0−9的数字、加法‘+’、减法‘-’、乘法‘*’、除法‘/’、小括号‘(’,‘)’、中括号‘[’,‘]’、大括号‘{’,‘}’组成,且运算符之间没有空格。输入描述:
输入一个长度为1≦len(s)≦10³、由题面所述符号构成的字符串,代表一个表达式。
输出描述:
输出一个整数ans,代表计算的答案。满足−10³≦ans≦10³。
解题思路:
ScriptEngine.eval(String script),实现表达式运算,这个属于奇技淫巧,正常是要用波兰表达式。
import java.util.*;
import javax.script.*;
public class Main {
public static void main(String[] args) throws ScriptException {
Scanner scan = new Scanner(System.in);
String input = scan.nextLine();
input = input.replace("[","(").replace("{","(").replace("}",")").replace("]",")");
ScriptEngine scriptEngine = new ScriptEngineManager().getEngineByName("nashorn");
System.out.println(scriptEngine.eval(input));
}
}HJ52 计算字符串的编辑距离
描述:
Levenshtein距离,又称编辑距离,指的是两个字符串之间,由一个转变成另一个所需的最少单字符编辑操作次数。被允许的转变包括:
- 对于任意一个字符串,在任意位置插入一个字符;
- 对于任意一个字符串,删除任意一个字符;
- 对于任意一个字符串,替换任意一个字符。
现在,对于给定的字符串s和t,请计算出它们的编辑距离。
输入描述:
第一行输入一个长度为1≦len(s)≦10³,仅由小写字母组成的字符串s。
第二行输入一个长度为1≦len(t)≦10³,仅由小写字母组成的字符串t。输出描述:
输出一个整数,表示s和t的编辑距离。
解题思路:
动态规划法,核心代码为字符匹配, s[i] = t[j],则 dp[i][j] = dp[i-1][j-1],字符不匹配,则dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + 1)
dp[i-1][j] + 1, # 删除s[i]
dp[i][j-1] + 1, # 在s中插入t[j]
dp[i-1][j-1] + 1 # 将s[i]替换为t[j]
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
String t = in.nextLine();
int[][] dp = new int[s.length() + 1][t.length() + 1];
for (int i = 0; i <= s.length(); i++){
dp[i][0] = i;
}
for (int i = 0; i <= t.length(); i++){
dp[0][i] = i;
}
for (int i = 1; i <= s.length(); i++){
for (int j = 1; j <= t.length(); j++){
if (s.charAt(i - 1) == t.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(dp[i - 1][j] + 1, Math.min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1));
}
}
}
System.out.println(dp[s.length()][t.length()]);
}
}HJ55 挑7
描述:
你需要统计1到n之间与7有关的数字的个数。
与7有关的数字包括:
- 是7的倍数(如 7,14,217,14,21 等);
- 包含数字7(如 17,27,37,⋯ ,70,71,72,⋯ 等)。
输入描述:
输入一个整数n(1≦n≦3×10⁴)。
输出描述:
输出一个整数,代表区间内与7有关的数字的个数。
解题思路:
i % 7,看是否是i的倍数,String.contains(CharSequence s),看是否包括7的字符串
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int result = 0;
String temp = "";
for (int i = 1; i < n + 1; i++) {
temp = i + "";
if (i % 7 == 0 || temp.contains("7")) {
result++;
}
}
System.out.println(result);
}
}HJ57 高精度整数加法
描述:
输入两个超大整数a,b,计算它们的和。
输入描述:
输入两个整数a,b(0≦a,b<10¹⁰⁰⁰⁰)。
输出描述:
输出一个整数,表示a和b的和。
解题思路:
BigDecimal.add(BigDecimal augend),实现高精度整数加法
import java.util.*;
import java.math.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s1 = in.nextLine();
String s2 = in.nextLine();
BigDecimal b1 = new BigDecimal(s1);
BigDecimal b2 = new BigDecimal(s2);
System.out.println(b1.add(b2));
}
}HJ59 找出字符串中第一个只出现一次的字符
描述:
对于给定的字符串,找出第一个只出现一次的字符。如果不存在,则输出−1。
输入描述:
在一行上输入一个长度为1≦len(s)≦10³、仅由小写字母构成的字符串s。
输出描述:
如果存在只出现一次的字符,输出第一个满足条件的字符;否则,直接输出−1。
解题思路:
字符串转字符数组,遍历数组,LinkedHashMap,实现map按插入顺序排序,遍历map,获取第一个出现次数为1的字符
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.next().toCharArray();
Map<Character, Integer> map = new LinkedHashMap<>();
for (int i = 0; i < chars.length; i++) {
map.put(chars[i], map.getOrDefault(chars[i], 0) + 1);
}
for (Character key: map.keySet()) {
if (map.get(key) == 1) {
System.out.println(key);
return;
}
}
System.out.println(-1);
}
}HJ63 DNA序列
描述:
一个 DNA 序列由 A/C/G/T 四个字母的排列组合组成。 G 和 C 的比例(定义为 GC-Ratio )是序列中 G 和 C 两个字母的总的出现次数除以总的字母数目(也就是序列长度)。在基因工程中,这个比例非常重要。因为高的 GC-Ratio 可能是基因的起始点。
给定一个很长的 DNA 序列,以及限定的子串长度 N ,请帮助研究人员在给出的 DNA 序列中从左往右找出 GC-Ratio 最高且长度为 N 的第一个子串。
DNA序列为 ACGT 的子串有: ACG , CG , CGT 等等,但是没有 AGT , CT 等等
数据范围:字符串长度满足1≤n≤1000,输入的字符串只包含 A/C/G/T 字母
输入描述:
输入一个string型基因序列,和int型子串的长度
输出描述:
找出GC比例最高的子串,如果有多个则输出第一个的子串
解题思路:
字符串转字符数组,如果长度等于字符串长度,直接返回字符串,否则两层遍历字符数组,找出符合长度要求,且C和G最多的字符串。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String string = in.next();
char[] chars = string.toCharArray();
int n = in.nextInt();
int max = 0;
String result = "";
if (n == chars.length) {
System.out.println(string);
return;
}
for (int i = 0; i < chars.length - n; i++) {
int temp = 0;
StringBuffer sb = new StringBuffer();
for (int j = i; j < i + n; j++) {
sb.append(chars[j]);
if (chars[j] == 'C' || chars[j] == 'G') {
temp++;
}
}
if (temp > max) {
max = temp;
result = sb.toString();
}
}
System.out.println(result);
}
}HJ64 MP3光标位置
描述:
MP3 Player因为屏幕较小,显示歌曲列表的时候每屏只能显示几首歌曲,用户要通过上下键才能浏览所有的歌曲。为了简化处理,假设每屏只能显示4首歌曲,光标初始的位置为第1首歌。
现在要实现通过上下键控制光标移动来浏览歌曲列表,控制逻辑如下:
歌曲总数<=4的时候,不需要翻页,只是挪动光标位置。
光标在第一首歌曲上时,按Up键光标挪到最后一首歌曲;光标在最后一首歌曲时,按Down键光标挪到第一首歌曲。
其他情况下用户按Up键,光标挪到上一首歌曲;用户按Down键,光标挪到下一首歌曲。
2. 歌曲总数大于4的时候(以一共有10首歌为例):
特殊翻页:屏幕显示的是第一页(即显示第1 – 4首)时,光标在第一首歌曲上,用户按Up键后,屏幕要显示最后一页(即显示第7-10首歌),同时光标放到最后一首歌上。同样的,屏幕显示最后一页时,光标在最后一首歌曲上,用户按Down键,屏幕要显示第一页,光标挪到第一首歌上。
一般翻页:屏幕显示的不是第一页时,光标在当前屏幕显示的第一首歌曲时,用户按Up键后,屏幕从当前歌曲的上一首开始显示,光标也挪到上一首歌曲。光标当前屏幕的最后一首歌时的Down键处理也类似。
其他情况,不用翻页,只是挪动光标就行。
数据范围:命令长度1≤s≤100,歌曲数量1≤n≤150
进阶:时间复杂度:O(n) ,空间复杂度:O(n)
输入描述:
输入说明:
1 输入歌曲数量
2 输入命令 U或者D输出描述:
输出说明
1 输出当前列表
2 输出当前选中歌曲
解题思路:
按照n的长度,如果n小于等于4,则只需要跟踪local,如果大于4,需要在整个列表第一行和最后一行,以及当前窗口第一行和最后一行发生改变的时候,修改start和end,同时也需要跟踪local
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int start = 1;
int end = 4;
int local = 1;
char[] arr = in.next().toCharArray();
if (n < 4) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == 'U') {
local--;
}
if (arr[i] == 'D') {
local++;
}
}
if (local <= 0) {
local = n;
} else if (local > n) {
local = 1;
}
for (int j = 1; j <= n; j++) {
if (j != n) {
System.out.print(j);
System.out.print(" ");
} else {
System.out.println(j);
}
}
System.out.println(local);
return;
}
for (int i = 0; i < arr.length; i++) {
if (arr[i] == 'U') {
local--;
}
if (arr[i] == 'D') {
local++;
}
if (local <= 0) {
local = n;
end = n;
start = n - 3;
} else if (local > n) {
local = 1;
start = 1;
end = 4;
}
if (local < start) {
start--;
end--;
}
if (local > end) {
start++;
end++;
}
}
for (int j = start; j <= end; j++) {
if (j != end) {
System.out.print(j);
System.out.print(" ");
} else {
System.out.println(j);
}
}
System.out.println(local);
}
}HJ65 查找两个字符串a,b中的最长公共子串
描述:
对于给定的两个字符串s和t,你需要找出它们的最长公共子串。特别地,如果存在多个答案,输出在较短串中最先出现的那个。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。
如果字符串a的一个子串a′与字符串b的一个子串b′完全相等,那么子串a′,b′是字符串a,b的一个公共子串。输入描述:
第一行输入一个长度为1≦len(s)≦300、仅由小写字母组成的字符串s。
第二行输入一个长度为1≦len(t)≦300、仅由小写字母组成的字符串t。输出描述:
输出一个字符串,代表s和t的最长公共子串。如果存在多个答案,输出在较短串中最先出现的那个。
解题思路:
双层循环,对长度小的字符串进行分解,从第0位开始,依次增加字符,然后去长串查询是否包含,然后再从第1位开始,依次增加字符,最后获取最长公共子串
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNext()) {
String str1 = in.nextLine();
String str2 = in.nextLine();
String so;
String lo;
if (str1.length() < str2.length()) {
so = str1;
lo = str2;
} else {
so = str2;
lo = str1;
}
int temp = 0;
String res = "";
for (int i = 0; i < so.length(); i++) {
for (int j = 0; j < so.length() - i; j++) {
String sub = so.substring(i, i + j + 1);
if (lo.contains(sub)) {
if (sub.length() > temp) {
temp = sub.length();
res = sub;
}
}
}
}
System.out.println(res);
}
}
}HJ66 配置文件恢复
描述:
有6条配置命令,它们执行的结果分别是:
命 令 执 行 reset reset what reset board board fault board add where to add board delete no board at all reboot backplane impossible backplane abort install first he he unknown command 注意:he he不是命令。
为了简化输入,方便用户,以“最短唯一匹配原则”匹配(注:需从首字母开始进行匹配):
- 若只输入一字串,则只匹配一个关键字的命令行。例如输入:r,根据该规则,匹配命令reset,执行结果为:reset what;输入:res,根据该规则,匹配命令reset,执行结果为:reset what;
- 若只输入一字串,但匹配命令有两个关键字,则匹配失败。例如输入:reb,可以找到命令reboot backpalne,但是该命令有两个关键词,所有匹配失败,执行结果为:unknown command
- 若输入两字串,则先匹配第一关键字,如果有匹配,继续匹配第二关键字,如果仍不唯一,匹配失败。例如输入:r b,找到匹配命令reset board 和 reboot backplane,执行结果为: unknown command。例如输入:b a,无法确定是命令board add还是backplane abort,匹配失败。
- 若输入两字串,则先匹配第一关键字,如果有匹配,继续匹配第二关键字,如果唯一,匹配成功。例如输入:bo a,确定是命令board add,匹配成功。
- 若输入两字串,第一关键字匹配成功,则匹配第二关键字,若无匹配,失败。例如输入:b addr,无法匹配到相应的命令,所以执行结果为:unknow command。
- 若匹配失败,打印“unknown command”
注意:有多组输入。
数据范围:数据组数:1≤t≤800,字符串长度1≤s≤20
进阶:时间复杂度:O(n),空间复杂度:O(n)
输入描述:
多行字符串,每行字符串一条命令
输出描述:
执行结果,每条命令输出一行
解题思路:
按照题目要求,获取Map里的key,进行比较,如果输入单词和key中单词数量相同,且String.startsWith(String prefix)可以匹配成功,则成功匹配数量+1,最后判断成功数量是不是1,输出value或错误信息
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
HashMap<String, String> map = new HashMap<>();
map.put("reset", "reset what");
map.put("reset board", "board fault");
map.put("board add", "where to add");
map.put("board delete", "no board at all");
map.put("reboot backplane", "impossible");
map.put("backplane abort", "install first");
String input;
while (in.hasNextLine()) {
int count = 0;
String key = "";
input = in.nextLine();
String[] inputArr = input.split(" ");
Set<String> set = map.keySet();
for (String str : set) {
String[] keyArr = str.split(" ");
if (inputArr.length == keyArr.length) {
if (inputArr.length == 1) {
if (keyArr[0].startsWith(inputArr[0])) {
count++;
key = str;
}
} else if (keyArr.length == 2) {
if (keyArr[0].startsWith(inputArr[0]) && keyArr[1].startsWith(inputArr[1])) {
count++;
key = str;
}
}
}
}
if (count == 1) {
System.out.println(map.get(key));
} else {
System.out.println("unknown command");
}
}
}
}HJ67 24点游戏算法
描述:
对于给定的四个小于10的正整数,你需要计算它们能否通过计算得到数字24。让我们来回忆标准二十四点游戏的规则:
- 输入的数字可能会重复,每一个数字必须用且只能用一次;
- 运算顺序可以任意安排,且可以使用括号进一步地改变运算优先级;
- 允许使用加、减、乘、除四种算数运算符,其中除法是实数除法;
如果可以得到24,输出true,否则,直接输出false。
输入描述:
在一行上输入四个整数a,b,c,d(1≦a,b,c,d≦10)代表等待计算的数字。
输出描述:
如果可以通过规定的计算得到24,输出true,否则,直接输出false。
解题思路:
使用DFS算法,深度遍历
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int[] nums = new int[4];
for (int i = 0; i < 4; i++) {
nums[i] = in.nextInt();
}
System.out.println(Main.canGet24(nums));
}
private static boolean canGet24(int[] nums) {
List<Double> list = new ArrayList<>();
for (int num : nums) {
list.add((double) num);
}
return dfs(list);
}
private static boolean dfs(List<Double> list) {
if (list.size() == 1) {
return Math.abs(list.get(0) - 24) < 1e-6;
}
for (int i = 0; i < list.size(); i++) {
for (int j = i + 1; j < list.size(); j++) {
double a = list.get(i);
double b = list.get(j);
List<Double> nextValues = new ArrayList<>();
nextValues.add(a + b);
nextValues.add(a - b);
nextValues.add(b - a);
nextValues.add(a * b);
if (Math.abs(b) > 1e-6) nextValues.add(a / b);
if (Math.abs(a) > 1e-6) nextValues.add(b / a);
for (double value : nextValues) {
List<Double> nextList = new ArrayList<>();
nextList.add(value);
for (int k = 0; k < list.size(); k++) {
if (k != i && k != j) {
nextList.add(list.get(k));
}
}
if (dfs(nextList)) {
return true;
}
}
}
}
return false;
}
}HJ69 矩阵乘法
描述:
对于给定的x行y列的矩阵:
和y行z列的矩阵:
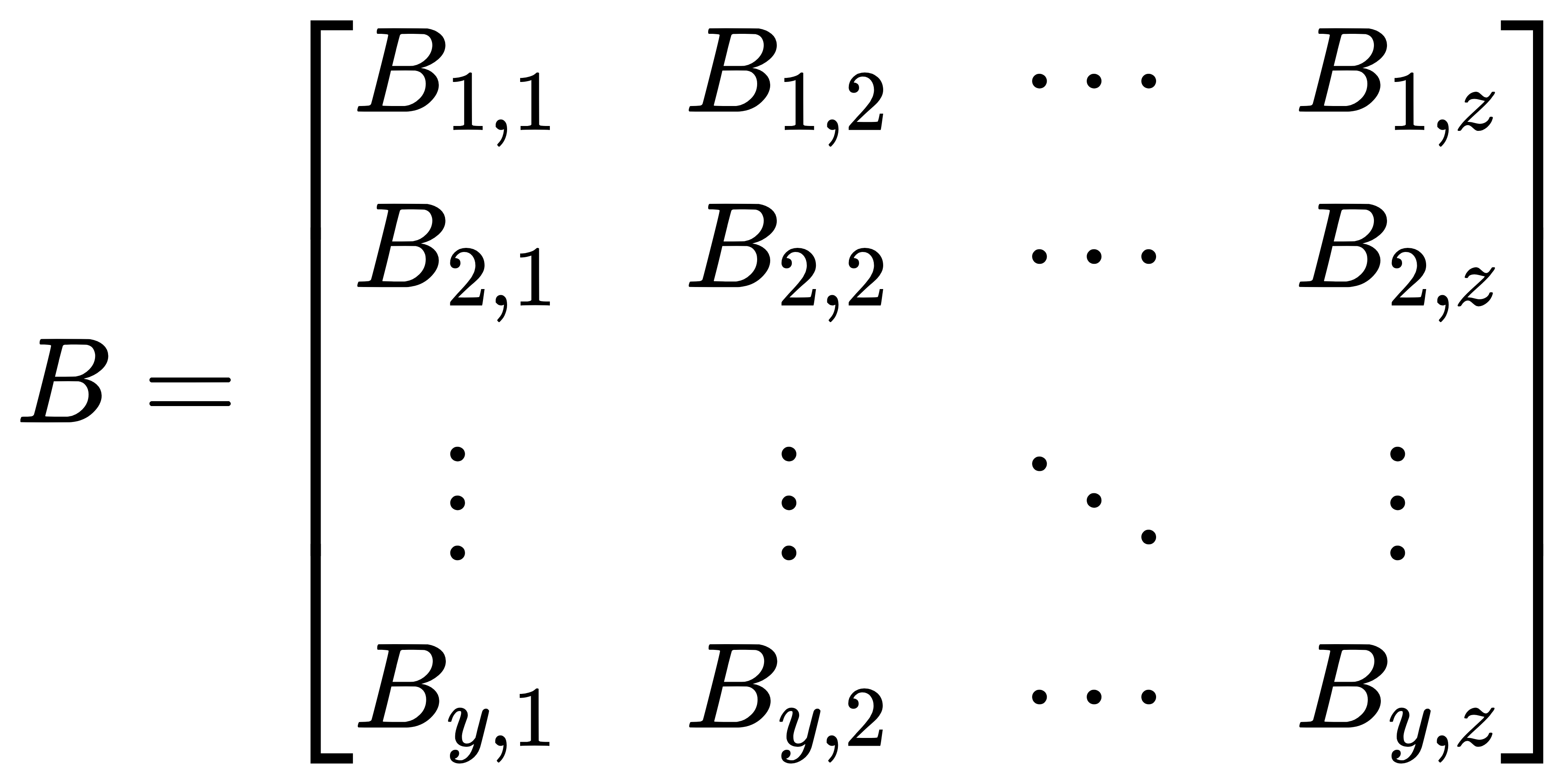
计算矩阵A和矩阵B的乘积C。
让我们回忆矩阵乘法的计算,对于第i行第j列的元素Cᵢ,ⱼ(1≦i≦x;1≦j≦z),有:
输入描述:
第一行输入一个整数x(1≦x≦100)代表第一个矩阵的行数。
第二行输入一个整数y(1≦y≦100)代表第一个矩阵的列数和第二个矩阵的行数。
第三行输入一个整数z(1≦z≦100)代表第二个矩阵的列数。
此后x行,第i行输入y个整数(0≦Aᵢ,ⱼ≦10)代表矩阵A的第i行元素。
此后y行,第i行输入z个整数(0≦Bᵢ,ⱼ≦10)代表矩阵B的第i行元素。
输出描述:
输出x行,第i行输出z个整数,代表矩阵C的第i行元素。
解题思路:
核心为temp += a1[i][k] * a2[k][j]
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int x = in.nextInt();
int y = in.nextInt();
int z = in.nextInt();
int[][] a1 = new int[x][y];
int[][] a2 = new int[y][z];
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
a1[i][j] = in.nextInt();
}
}
for (int i = 0; i < y; i++) {
for (int j = 0; j < z; j++) {
a2[i][j] = in.nextInt();
}
}
for (int i = 0; i < x; i++) {
for (int j = 0; j < z; j++) {
int temp = 0;
for (int k = 0; k < y; k++) {
temp += a1[i][k] * a2[k][j];
}
if (j != z - 1){
System.out.print(temp + " ");
}else {
System.out.println(temp);
}
}
}
}
}HJ70 矩阵乘法计算量估算
描述:
对于给定的a行b列的矩阵:
和b行c列的矩阵:
和c行d列的矩阵:
在计算A×B×C时,不同的运算顺序会带来不同的运算量。例如,(A×B)×C的运算量是a×b×c+a×c×d,而A×(B×C)的运算量是 b×c×d+a×b×d。
现在,对于给定的n个矩阵的大小与运算式,请你计算出所需要的运算量。输入描述:
第一行输入一个整数n(1≦n≦15)代表矩阵的个数。
此后n行,第i行输入两个整数ai和bi(1≦ai,bi≦100)代表第i个矩阵的行数和列数。
最后一行输入一个长度为1≦len(s)≦10³的字符串s代表运算式。运算式中只包含前n个大写字母与括号,第i个大写字母对应输入的第i个矩阵,括号成对出现,保证运算式合法且正确。输出描述:
在一行上输出一个整数,代表计算需要的运算量。
解题思路:
使用栈存放矩阵行数和列数,倒序遍历字符串,属于字母则把相应的矩阵列数和行数入栈,属于括号(则推出计算,pop出x0,y0,x1,y1,累加x0 * y0 * y1,然后再push入y1,x0
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int a[][] = new int[n][2];
for (int i = 0; i < n; i++) {
a[i][0] = in.nextInt();
a[i][1] = in.nextInt();
}
String s = in.next();
// 存放矩阵行数和列数
Stack<Integer> stack = new Stack();
int sum = 0;
for (int i = s.length() - 1, j = n - 1; i >= 0; i--) {
// 属于字母则把相应的矩阵列数和行数入栈
if (s.charAt(i) >= 'A' && s.charAt(i) <= 'Z') {
stack.push(a[j][1]);
stack.push(a[j][0]);
j--;
// 括号:推出计算
} else if (s.charAt(i) == '(') {
// 矩阵尺寸x0*y0
int x0 = stack.pop();
int y0 = stack.pop();
// 矩阵尺寸x1*y1
int x1 = stack.pop();
int y1 = stack.pop();
// 两个矩阵的乘法次数为x0*y0*y1或x0*x1*y1(其中y0==x1)
sum += x0 * y0 * y1;
// 把相乘后得到的矩阵列数入栈
stack.push(y1);
// 把相乘后得到的矩阵行数入栈
stack.push(x0);
}
}
System.out.println(sum);
}
}HJ71 字符串通配符
描述:
在计算机中,通配符是一种特殊语法,广泛应用于文件搜索、数据库、正则表达式等领域。让我们来学习通配符的匹配规则:
- ‘*’ 符号代表匹配0个或以上的数字或字母;
- ‘?’ 符号代表匹配1个数字或字母;
- 小写字母字符代表匹配自身和自身的大写字母形态;
- 大写字母字符代表匹配自身和自身的小写字母形态;
- 其他字符代表匹配自身。
现在,对于给定的通配符字符串s和目标字符串p,不考虑大小写,请判断s是否可以匹配得到p。如果可以,输出true;否则,输出false。
在本题中,给定的字符串由ASCII码在33到126范围内的可见字符构成。您可以参阅下表获得其详细信息(您可能关注的内容是,这其中不包含空格、换行)。输入描述:
第一行输入一个长度为1≦len(s)≦100、由可见字符构成的通配符字符串s。
第二行输入一个长度为1≦len(p)≦100、由可见字符构成的目标字符串p。输出描述:
如果可以匹配得到,输出true;否则,输出false。
解题思路:
多个*改为1个*,将?改为[0-9a-z]{1},将*改为[0-9a-z]{0,},然后匹配
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String value = in.next().toLowerCase(Locale.ROOT);
String target = in.next().toLowerCase(Locale.ROOT);
String regx = value.replaceAll("\\*{2,}", "\\*");
regx = regx.replaceAll("\\?", "[0-9a-z]{1}");
regx = regx.replaceAll("\\*", "[0-9a-z]{0,}");
System.out.println(target.matches(regx));
}
}HJ74 参数解析
描述:
在命令行输入如下命令:
xcopy /s c:\\ d:\\e,
各个参数如下:
参数1:命令字xcopy
参数2:字符串/s
参数3:字符串c:\\
参数4: 字符串d:\\e
请编写一个参数解析程序,实现将命令行各个参数解析出来。
解析规则:
- 参数分隔符为空格
- 对于用""包含起来的参数,如果中间有空格,不能解析为多个参数。比如在命令行输入xcopy /s "C:\\program files" "d:\"时,参数仍然是4个,第3个参数应该是字符串C:\\program files,而不是C:\\program,注意输出参数时,需要将""去掉,引号不存在嵌套情况。
- 参数不定长
- 输入由用例保证,不会出现不符合要求的输入
数据范围:字符串长度:1≤s≤1000
进阶:时间复杂度:O(n),空间复杂度:O(n)
输入描述:
输入一行字符串,可以有空格
输出描述:
输出参数个数,分解后的参数,每个参数都独占一行
解题思路:
字符串转字符数组,遍历数组,如果遍历时碰到",进行flag标识,如果标识是true,代表已经有一组",或者没有",可以认为是分割符号,如果标识是flase,代表在一组"之内,不能认为是分割符号
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.nextLine().toCharArray();
List<String> list = new ArrayList<>();
StringBuffer sb = new StringBuffer();
boolean flag = true;
for (int i = 0; i < chars.length; i++) {
if (chars[i] != ' ' && chars[i] != '\"') {
sb.append(chars[i]);
} else if (chars[i] == ' ') {
if (flag) {
list.add(sb.toString());
sb = new StringBuffer();
} else {
sb.append(chars[i]);
}
} else if (chars[i] == '\"') {
flag = !flag;
}
if (i == chars.length - 1) {
list.add(sb.toString());
sb = new StringBuffer();
}
}
System.out.println(list.size());
for (int i = 0; i < list.size(); i++) {
System.out.println(list.get(i));
}
}
}HJ75 公共子串计算
描述:
对于给定的两个字符串s和t,你需要找出它们的最长公共子串的长度。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。
如果字符串a的一个子串a′与字符串b的一个子串b′完全相等,那么子串a′,b′是字符串a,b的一个公共子串。输入描述:
第一行输入一个长度为1≦len(s)≦150、仅由小写字母组成的字符串s。
第二行输入一个长度为1≦len(t)≦150、仅由小写字母组成的字符串t。输出描述:
输出一个整数,代表s和t的最长公共子串的长度。
解题思路:
动态规划法:核心为当str1[i-1] == str2[j-1]时,dp[i][j] = dp[i-1][j-1] + 1,延续前一个位置的公共子串,否则dp[i][j] = 0
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str1 = in.nextLine();
String str2 = in.nextLine();
int[][] dp = new int[str1.length() + 1][str2.length() + 1];
int max = 0;
for (int i = 1; i <= str1.length(); i++) {
for (int j = 1; j <= str2.length(); j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
max = Math.max(max, dp[i][j]);
}
}
}
System.out.println(max);
}
}HJ77 火车进站
描述:
火车站一共有n辆火车需要入站,每辆火车有一个编号,编号为1到n。
同时,也有火车需要出站,由于火车站进出共享一个轨道,所以后入站的火车需要先出站。换句话说,对于某一辆火车,只有在它之后入站的火车都出站了,它才能出站。
现在,已经知道了火车的入站顺序,你需要计算,一共有多少种不同的出站顺序。按照字典序从小到大依次输出全部的出站顺序。输入描述:
第一行输入一个整数n(1≦n≦10)代表火车的数量。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦n)代表火车的入站顺序。输出描述:
输出若干行,每行输出n个整数,代表一种出站顺序。你需要按照字典序从小到大依次输出。
解题思路:
利用入栈再出栈,两个栈解决问题
import java.util.*;
public class Main {
private static Stack<String> stack1 = new Stack<>();
private static Stack<String> stack2 = new Stack<>();
private static List<String> list = new ArrayList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
int n = scanner.nextInt();
scanner.nextLine();
String string = scanner.nextLine();
String[] strings = string.split(" ");
for (int i = strings.length - 1; i >= 0; i--) {
stack1.push(strings[i]);
}
ff("");
Collections.sort(list);
for (String s : list) {
System.out.println(s);
}
}
}
public static void ff(String str) {
if (stack1.isEmpty() && stack2.isEmpty()) {
list.add(str.trim());
return;
}
if (!stack2.isEmpty()) {
String str1 = stack2.pop();
ff(str + " " + str1);
stack2.push(str1);
}
if (!stack1.isEmpty()) {
stack2.push(stack1.pop());
ff(str);
stack1.push(stack2.pop());
}
}
}HJ82 将真分数分解为埃及分数
描述:
定义分子为1的分数为埃及分数,例如1/2,1/100等。
现在,对于给定的一个分子小于分母的分数a/b,请将其分解为若干个不同的埃及分数之和。随后,使用1/b₁+1/b₂+⋯+1/bₙ的格式输出结果,其中,b₁,b₂,…,bₙ表示每一个埃及分数的分母。输入描述:
以a/b的格式输入一个分数a/b,其中1≦a<b≦100。不保证分数为最简分数。
输出描述:
以1/b₁+1/b₂+⋯+1/bₙ的格式输出结果,其中,b₁,b₂,…,bₙ表示每一个埃及分数的分母。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。
解题思路:
使用贪心算法,每次找到不超过当前分数的最大埃及分数,然后从原分数中减去,重复这个过程直到分子为1。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] input = in.next().split("/");
long a = Long.parseLong(input[0]);
long b = Long.parseLong(input[1]);
while (a != 1) {
// 计算 b/a 的整数部分
long p = b / a;
// 计算 b/a 的余数
long r = b % a;
System.out.printf(1 + "/" + (p + 1) + "+");
// 更新分子
a = a - r;
// 更新分母
b = b * (p + 1);
if (a == 1 || b % a == 0) {
// 简化分母
b = b / a;
break;
}
}
System.out.printf(1 + "/" + b);
}
}HJ83 仰望水面的歪
描述:
小歪正在水底潜水,他所在的位置距离水面的直线距离为h。小歪有一个神奇的激光装置,激光射向水面后会发生全反射现象。
以小歪所在的位置为原点建立三维坐标轴,小歪的坐标即为(0,0,0)。在水中,有一些坐标需要小歪使用激光击中,第i个坐标使用(xᵢ,yᵢ,zᵢ)表示。求解,对于每一个坐标,小歪需要以什么向量方向射出激光,使得经过一次水面全反射后恰好击中它。输入描述:
第一行输入两个整数n,h(1≦n≦100; 1≦h≦10⁹)代表需要击中的坐标位置数量、距离水面的距离。
随后n行,每行输入三个整数x,y,z(1≦x,y≦10⁹;−10⁹≦z≦h)代表需要击中的坐标。输出描述:
对于每一个坐标,在一行上输出三个整数i,j,k,代表射出向量方向,你需要保证gcd(i,j,k)=1。
解题思路:
几何知识,向某个位置发射射线,targetx和targety分别与x和y一致,
targetz = 2 * h - z,画图出来即可。然后就targetx,targety,targetz的最大公约数cd,分别把targetx,targety,targetz三个数除cd并返回即可。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
long h = in.nextInt();
for (int i = 0; i < n; i++) {
long x = in.nextLong();
long y = in.nextLong();
long z = in.nextLong();
long targetZ = 2 * h - z;
long cd = gcd(x, gcd(y, targetZ));
System.out.println(x / cd + " " + y / cd + " " + targetZ / cd);
}
}
private static long gcd(long x, long y) {
if (y == 0) {
return x;
} else {
return gcd(y, x % y);
}
}
}HJ90 合法IP
描述:
IPV4地址可以用一个32位无符号整数来表示,一般用点分方式来显示,点将IP地址分成4个部分,每个部分为8位,表示成一个无符号整数(因此正号不需要出现),如10.137.17.1,是我们非常熟悉的IP地址,一个IP地址串中没有空格出现(因为要表示成一个32数字)。
现在需要你用程序来判断IP是否合法。
数据范围:数据组数:1≤t≤18
进阶:时间复杂度:O(n),空间复杂度:O(n)
输入描述:
输入一个ip地址,保证不包含空格
输出描述:
返回判断的结果YES or NO
解题思路:
按"\\."拆分字符串数组,要求字符串数组长度必须为4,各个字符串不能为空字符串,必须在0到255之间,且首位数为0时,整个数字只能为0
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] s = in.nextLine().split("\\.");
if (s.length != 4) {
System.out.println("NO");
return;
}
for (int i = 0; i < s.length; i++) {
char[] chars = s[i].toCharArray();
if (chars.length == 0) {
System.out.println("NO");
return;
}
for (int j = 0; j < chars.length; j++) {
if (!Character.isDigit(chars[j])) {
System.out.println("NO");
return;
}
}
Integer integer = Integer.parseInt(new String(chars));
if (integer > 255 || integer < 0) {
System.out.println("NO");
return;
}
if (chars[0] == '0' && integer != 0) {
System.out.println("NO");
return;
}
}
System.out.println("YES");
}
}HJ92 在字符串中找出连续最长的数字串
描述:
对于给定的由数字和小写字母混合构成的字符串s,找到其中最长的数字子串。如果由多个相同长度的数字子串,则需要全部输出,具体输出的格式请参考输出描述。
子串为从原字符串中,连续的选择一段字符(可以全选、可以不选)得到的新字符串。输入描述:
输入一个长度为1≦len(s)≦200、由数字和小写字母混合构成的字符串s。保证至少存在一个数字子串。
输出描述:
记最长的数字子串长度为l,有m个长度为l的数字子串。在一行上先首尾相连的输出m个长度为l的数字子串(不使用空格分割),随后输出一个逗号,再输出l。
解题思路:
字符串转字符数组,然后遍历字符数组,碰到数字字符,增加记录,继续遍历,碰到非数字字符,进行比较长短和更新结果
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chars = in.next().toCharArray();
int max = 0;
int temp = 0;
StringBuffer result = new StringBuffer();
StringBuffer tempSb = new StringBuffer();
for (int i = 0; i < chars.length; i++) {
if (Character.isDigit(chars[i])) {
tempSb.append(chars[i]);
temp++;
} else {
if (temp > max) {
max = temp;
result = tempSb;
} else if (temp == max && temp != 0) {
result.append(tempSb);
}
tempSb = new StringBuffer();
temp = 0;
}
if (i == chars.length - 1) {
if (temp > max) {
max = temp;
result = tempSb;
} else if (temp == max && temp != 0) {
result.append(tempSb);
}
}
}
System.out.println(result + "," + max);
}
}HJ98 喜欢切数组的红
描述:
小红有一个长度为n的数组{a₁,a₂,…,aₙ},她打算将数组切两刀变成三个非空子数组,使得每一个子数组中至少存在一个正数,且每个子数组的和都相等。
看起来不是很难,所以小红想让你求解,一共有多少种不同的切分方案。输入描述:
第一行输入两个整数n(3≦n≦2×10⁵)代表数组中的元素数量。
第二行输入n个整数a₁,a₂,…,aₙ(−10⁹≦aᵢ≦10⁹)代表数组元素。输出描述:
在一行上输出一个整数,代表切分方案数。
解题思路:
先对总和%3,如果不为0,则一定不可能成立,然后对数组长度为3的,进行判断,然后双层循环,对数组进行遍历,只需要判断第1部分和第2部分,等于平均值就行
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] ints = new int[n];
int total = 0;
for (int i = 0; i < n; i++) {
ints[i] = in.nextInt();
total += ints[i];
}
if (total % 3 != 0) {
System.out.println(0);
return;
}
if (n == 3) {
if (ints[0] == ints[1] && ints[1] == ints[2]) {
System.out.println(1);
} else {
System.out.println(0);
}
return;
}
int avg = total / 3;
int result = 0;
int total1 = 0;
int max1 = 0;
for (int i = 0; i < n - 2; i++) {
total1 += ints[i];
max1 = Math.max(max1, ints[i]);
if (total1 == avg && max1 > 0) {
int total2 = 0;
int max2 = 0;
for (int j = i + 1; j < n - 1; j++) {
total2 += ints[j];
max2 = Math.max(max2, ints[j]);
if (total2 == avg && max2 > 0) {
result++;
}
}
}
}
System.out.println(result);
}
}HJ103 Redraiment的走法
描述:
Redraiment 是走梅花桩的高手。现在,地上有n个梅花桩排成一排,从前到后高度依次为h₁,h₂,…,hₙ。
Redraiment可以任选一个梅花桩开始,向后跳到任意一个比当前高度高的梅花桩上。
求Redraiment最多可以跳过多少个梅花桩。输入描述:
第一行输入一个整数n(1≦n≦200)代表梅花桩的数量。
第二行输入n个整数h₁,h₂,…,hₙ(1≦hᵢ≦350)代表每一个梅花桩的高度。输出描述:
输出一个正整数,代表Redraiment最多可以跳过多少个梅花桩。
解题思路:
本质依旧是最长递增序列
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] dp = new int[n];
int[] map = new int[n];
for (int i = 0; i < n; i++) {
map[i] = in.nextInt();
}
Arrays.fill(dp, 1);
int max = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (map[i] > map[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
max = Math.max(dp[i], max);
}
}
}
System.out.println(max);
}
}HJ104 小红的矩阵染色
描述:
小红拿到了一个矩阵,初始有一些格子被染成了黑色。现在小红希望把最多k个未被染成黑色的格子染成红色,具体的计分方式是:如果一个红色格子下方相邻的格子也是红色,那么这个红色格子可以获得1分。
小红想知道,最多可以得到多少分?输入描述:
第一行输入三个正整数n,m,k,代表矩阵的行数和列数、以及小红最多可以染色的格子数量。
接下来的n行,每行输入一个长度为m的字符串,用来表示矩阵的初始染色情况。'*'字符代表黑色,'o'字符代表白色。
1≤n,m≤1000
1≤k≤n∗m输出描述:
一个整数,代表小红可以获得的最大分数。
解题思路:
和HJ 172重复
HJ111 气球迷题
描述:
对于给定的n个气球,摆放成一排,颜色仅为红、黄、蓝中的一种。小红想要让颜色相同的气球连续的摆放在一起,为了达成这个目标,她需要将气球重新染色。第i个气球重新染成任意的颜色均需要tᵢ秒,询问需要消耗的最少时间是多少呢。
输入描述:
第一行输入一个整数n(1≦n≦2×10⁵)代表气球数量。
第二行输入一个长度为n的、仅由0,1,2构成的字符串代表气球的初始颜色。其中,0,1,2分别代表初始颜色为红、黄、蓝。
第三行输入n个整数t₁,t₂,…,tₙ(1≦tᵢ≦10⁷)代表气球重新染色需要的时间。输出描述:
在一行上输出一个整数,代表最少需要的染色时间。
解题思路:
利用动态规划方法,遍历15种组合方式,找出最小值
import java.util.*;
public class Main {
static final long INF = 1000000000000000L;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
String string = in.next();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
// dp[i][j] 表示前 i 个气球达成状态 j 的最小时间
// dp[0]表示000.. dp[1]表示111.. dp[2]表示222...
// dp[3]表示011.. dp[4]表示022.. dp[5]表示100... dp[6]表示122.. dp[7]表示200 dp[8]211
// dp[9]表示012.. dp[10]表示021.. dp[11]表示102... dp[12]表示120.. dp[13]表示201 dp[14]210
long[][] dp = new long[n + 1][15];
for (long[] row : dp) {
Arrays.fill(row, INF);
}
// 初始状态
dp[0][0] = 0;
dp[0][1] = 0;
dp[0][2] = 0;
for (int i = 1; i <= n; i++) {
int currentColor = string.charAt(i - 1) - '0';
int[] b = new int[3];
// 默认需要染色
Arrays.fill(b, a[i - 1]);
// 当前颜色无需染色
b[currentColor] = 0;
// 单色状态(全0、全1、全2)
dp[i][0] = dp[i - 1][0] + b[0];
dp[i][1] = dp[i - 1][1] + b[1];
dp[i][2] = dp[i - 1][2] + b[2];
// 双色状态(如 0->1, 0->2, 1->0 等)
if (i >= 2) {
// 0->1
dp[i][3] = Math.min(dp[i - 1][0], dp[i - 1][3]) + b[1];
// 0->2
dp[i][4] = Math.min(dp[i - 1][0], dp[i - 1][4]) + b[2];
// 1->0
dp[i][5] = Math.min(dp[i - 1][1], dp[i - 1][5]) + b[0];
// 1->2
dp[i][6] = Math.min(dp[i - 1][1], dp[i - 1][6]) + b[2];
// 2->0
dp[i][7] = Math.min(dp[i - 1][2], dp[i - 1][7]) + b[0];
// 2->1
dp[i][8] = Math.min(dp[i - 1][2], dp[i - 1][8]) + b[1];
}
// 三色状态(如 0->1->2, 0->2->1 等)
if (i >= 3) {
// 0->1->2
dp[i][9] = Math.min(dp[i - 1][3], dp[i - 1][9]) + b[2];
// 0->2->1
dp[i][10] = Math.min(dp[i - 1][4], dp[i - 1][10]) + b[1];
// 1->0->2
dp[i][11] = Math.min(dp[i - 1][5], dp[i - 1][11]) + b[2];
// 1->2->0
dp[i][12] = Math.min(dp[i - 1][6], dp[i - 1][12]) + b[0];
// 2->0->1
dp[i][13] = Math.min(dp[i - 1][7], dp[i - 1][13]) + b[1];
// 2->1->0
dp[i][14] = Math.min(dp[i - 1][8], dp[i - 1][14]) + b[0];
}
}
long ans = INF;
for (int i = 0; i < 15; i++) {
ans = Math.min(ans, dp[n][i]);
}
System.out.println(ans);
}
}HJ116 小红的排列构造②
描述:
小红定义一个仅由0和1两个字符构成的字符串s与一个长度为n的数组p为匹配,当且仅当满足下列两点:
- 若sᵢ=1,则数组{p₁,p₂,…,pᵢ}恰好构成一个排列;
- 若sᵢ=0,则数组{p₁,p₂,…,pᵢ}无法构成一个排列。
现在小红给出了一个长度为n的字符串s,请你构造一个长度为n的排列p使得s与p匹配;如果不存在这样的排列,请输出−1。
【名词解释】
排列:排列是由1∼n 这n个整数按任意顺序组成的数组,其中每个整数恰好出现一次。输入描述:
第一行输入一个整数n(1≦n≦10⁵)表示字符串及排列的长度。
第二行输入一个长度为n,仅由0和1构成的字符串s。输出描述:
如果不存在满足条件的排列,直接输出−1;否则,在一行上输出n个整数p₁,p₂,…,pₙ表示你构造出的排列。
如果存在多个满足条件的排列,输出任意一个均可,系统将自动判定其正确性。请注意,自测运行功能可能因此返回错误结果,请自行检查答案正确性。
解题思路:
以堆栈的思路来写,遍历字符串的每项,遍历到第i项则将i存入堆栈,若第i项为1则将堆栈内全部内容输出,否则不作操作
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
String s = in.next();
Stack<Integer> stack = new Stack<>();
if (s.charAt(n - 1) == '0') {
System.out.print(-1);
return;
}
for (int i = 1; i <= n; i++) {
stack.push(i);
if (s.charAt(i - 1) != '0') {
while (!stack.empty()) {
System.out.print(stack.pop() + " ");
}
}
}
}
}HJ117 小红的01子序列构造(easy)
描述:
给定一个仅由字符0,1组成的字符串s,长度为n。小红想找到一个闭区间[l,r]使得在子串 sₗ.ᵣ中,恰好存在k个严格等于01的子序列(即选取下标i<j,满足sᵢ=0, sⱼ=1)。
请你输出任意一个满足条件的区间;若不存在,则输出−1。
【名词解释】
子序列:从字符串中删除任意个(可为零)字符后得到的字符串,保留剩余字符原有相对顺序。输入描述:
第一行输入两个整数n,k(1≦n≦2×10⁵; 1≦k≦10¹⁰)——字符串长度与目标子序列数量。
第二行输入一个长度为n的01串s(下标从1开始)。输出描述:
若不存在满足要求的区间,输出单独一行-1;否则输出两个整数l,r(1≦l≦r≦n)表示区间端点(输出任意一组均可)。
解题思路:
滑动窗口,记录当前窗口的(0,1) 对数,如果超过k,缩减左侧窗口,看是否符合k,如果不符合,继续遍历,滑动窗口
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
long k = in.nextLong();
String s = in.next();
int l = 0;
// (0,1) 对数,可能很大
long count = 0;
// 当前窗口 [l, r] 中 '0' 的个数
int zeros = 0;
// 当前窗口 [l, r] 中 '1' 的个数
int ones = 0;
for (int r = 0; r < n; r++) {
// 将 s[r] 加入窗口
if (s.charAt(r) == '0') {
zeros++;
// s[r] == '1'
} else {
// 新 '1' 与前面所有 '0' 配对
count += zeros;
ones++;
}
// 尝试收缩左端点,寻找恰好为 k 的区间
while (count >= k && l <= r) {
if (count == k) {
System.out.println((l + 1) + " " + (r + 1));
return;
}
// 左移 l
if (s.charAt(l) == '0') {
// 移除 '0',它之前与窗口内所有 '1' 配对
count -= ones;
zeros--;
// s[l] == '1'
} else {
ones--;
}
l++;
}
}
// 如果没有找到
System.out.println(-1);
}
}HJ118 小红的二分图构造
描述:
小红希望你构造一个二分图,满足第i个节点的度数恰好等于dᵢ。你能帮帮她吗?
二分图是一张满足如下条件的图:它的节点可以被分成两个不相交的集合U与V,使得图中的每一条边都连接U中的一个节点与V中的一个节点。输入描述:
第一行输入一个正整数n(1≤n≤100),代表二分图的节点数量。
第二行输入n个正整数d₁,d₂,…,dₙ(1≤dᵢ≤n−1),代表每个节点的度数。输出描述:
如果答案不存在,直接输出−1 。
否则,请参考下方的格式输出。
第一行输出一个整数m代表边的数量。
接下来的m行,每行输出两个正整数u,v(1≤u,v≤n)代表节点u和节点v有一条边连接。
构造的图可以包含重边,但不能包含自环。构造的最终的图可以不连通,你只需要保证每个连通分量均为二分图。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。注意,自测运行功能可能因此返回错误结果,请自行检查答案正确性。
解题思路:
读取n和度数数组d。
计算总度数sum,如果sum为奇数,输出-1。
计算T = sum/2。
动态规划:使用二维布尔数组dp,大小为[n + 1][T + 1],初始dp[0][0]=true。
遍历每个节点,从T到d[i]更新dp。
如果dp[n][T]为false,输出-1。
否则,回溯确定每个节点属于U还是V。
将节点分为两个集合,并记录每个节点的度数。
使用循环,每次从U和V中选取度数最大的节点,连接一条边,然后减少这两个节点的度数,直到所有节点的度数变为0。
输出边。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] d = new int[n];
for (int i = 0; i < n; i++) {
d[i] = in.nextInt();
}
int totalDegree = Arrays.stream(d).sum();
if (totalDegree % 2 != 0) {
System.out.println(-1);
return;
}
int T = totalDegree / 2;
boolean[][] dp = new boolean[n + 1][T + 1];
dp[0][0] = true;
for (int i = 1; i <= n; i++) {
int dVal = d[i - 1];
for (int j = 0; j <= T; j++) {
if (j >= dVal) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - dVal];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
if (!dp[n][T]) {
System.out.println(-1);
return;
}
boolean[] group = new boolean[n];
int currentJ = T;
for (int i = n; i >= 1; i--) {
if (currentJ >= d[i - 1] && dp[i - 1][currentJ - d[i - 1]]) {
group[i - 1] = true;
currentJ -= d[i - 1];
} else {
group[i - 1] = false;
}
}
List<int[]> listU = new ArrayList<>();
List<int[]> listV = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (group[i]) {
listU.add(new int[]{i + 1, d[i]});
} else {
listV.add(new int[]{i + 1, d[i]});
}
}
List<String> edges = new ArrayList<>();
while (true) {
// 按度数降序排序
listU.sort((a, b) -> Integer.compare(b[1], a[1]));
listV.sort((a, b) -> Integer.compare(b[1], a[1]));
if (listU.get(0)[1] == 0) {
break;
}
int uNode = listU.get(0)[0];
int uDeg = listU.get(0)[1];
int vNode = listV.get(0)[0];
int vDeg = listV.get(0)[1];
edges.add(uNode + " " + vNode);
listU.set(0, new int[]{uNode, uDeg - 1});
listV.set(0, new int[]{vNode, vDeg - 1});
}
System.out.println(edges.size());
for (String edge : edges) {
System.out.println(edge);
}
}
}HJ128 小红的双生排列
描述:
小红定义一个排列是双生排列,当且仅当任意相邻两项之和均为奇数。
现在小红想知道,长度为 nn 的双生排列共有多少种?由于答案可能过大,请对10⁹+7取模。
长度为n的排列是由1∼n这n个整数、按任意顺序组成的数组,其中每个整数恰好出现一次。例如,{2,3,1,5,4}是一个长度为5的排列,而{1,2,2}和{1,3,4}都不是排列,因为前者存在重复元素,后者包含了超出范围的数。输入描述:
输入一个整数n(2≦n≦10⁵)代表排列的长度。
输出描述:
输出一个整数,代表长度为n的双生排列数量对10⁹+7取模的答案。
解题思路:
排列数计算:
n为偶数:2 × (奇数个数)! × (偶数个数)! = 2 × (ouShu)! × (ouShu)!
n为奇数:(奇数个数)! × (偶数个数)! = (ouShu+1)! × (ouShu)! = (ouShu)! × (ouShu)! × (ouShu+1),由于mod 1000000007L,代码如下
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int totalNums = in.nextInt();
long mod = 1000000007L;
int evenCount = totalNums / 2;
long res = 1;
for (int i = 2; i <= evenCount; i++) {
res = res * i % mod;
}
if (totalNums % 2 == 0) {
System.out.println((res * res * 2) % mod);
} else {
System.out.println(((res * res) % mod * (evenCount + 1)) % mod);
}
}
}HJ129 小红的双生数
描述:
小红定义一个正整数是“双生数”,当且仅当该正整数的每个数位的相邻数位中,恰好有一个和该数位的数字相同。
现在小红拿到了一个正整数x,她希望你求出不小于x的最小“双生数”。输入描述:
输入一个正整数x(1≦x≦10¹⁰⁰⁰⁰⁰)代表限制。
输出描述:
输出一个正整数,代表不小于x的最小“双生数”。该数字不包含前导零。
解题思路:
如果长度为奇数,直接循环添加1100,检查当前数字是否已经是双生数,如果已经是双生数,直接输出,如果当前两个不相等则更新为更大的那个,如果相等但是和前两位相同,则向前进位,如果首位是0,需要补11
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
char[] chs = in.nextLine().toCharArray();
StringBuilder sb = new StringBuilder();
// 如果长度为奇数,直接循环添加1100
boolean flag = true;
if (chs.length % 2 == 1) {
for (int i = 1; i <= chs.length; i += 2) {
if (flag) {
sb.append("11");
} else {
sb.append("00");
}
flag = !flag;
}
System.out.print(sb);
return;
}
int[] nums = new int[chs.length];
for (int i = 0; i < chs.length; i++) {
nums[i] = chs[i] - '0';
}
boolean valid = true;
// 检查当前数字是否已经是双生数
for (int i = 0; i < nums.length - 1; i += 2) {
if (nums[i] != nums[i + 1]) {
valid = false;
break;
}
if (i > 0 && nums[i] == nums[i - 1]) {
valid = false;
break;
}
}
if (valid) {
// 如果已经是双生数,直接输出
for (int num : nums) {
System.out.print(num);
}
return;
}
int changed = -1;
for (int i = 0; i < nums.length - 1; i += 2) {
if (changed != -1) {
nums[i] = changed;
nums[i + 1] = changed;
changed = (changed == 0 ? 1 : 0);
continue;
}
// 如果当前两个不相等则更新为更大的那个
if (nums[i] != nums[i + 1]) {
changed = 0;
nums[i] = Math.min(nums[i], nums[i + 1]) + 1;
nums[i + 1] = nums[i];
}
// 如果相等但是和前两位相同,则向前进位
while (i > 0 && nums[i] == nums[i - 1]) {
while (i >= 0 && nums[i] == 9) {
i -= 2;
}
if (i >= 0) {
nums[i]++;
nums[i + 1]++;
}
changed = 0;
}
}
if (nums[0] == 0) {
System.out.print("11");
}
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i]);
}
}
}HJ132 小红走网格
描述:
在二维平面坐标系中,小红初始位置为(0,0)。她可以向四个方向移动,移动的步数由四个正整数a、b、c、d 定义,分别表示小红向上、向下、向左和向右移动一次的步数。
- 向上移动一次,走a步:(0,0)→(0,a);
- 向下移动一次,走b步:(0,0)→(0,−b);
- 向左移动一次,走c步:(0,0)→(−c,0);
- 向右移动一次,走d步:(0,0)→(d,0)。
小红最终想要到达的目标位置为(x,y)。请判断小红是否可以通过上述步数到达目标位置。
输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦10⁴)代表数据组数,每组测试数据描述如下:
在一行上输入六个整数x,y,a,b,c,d(1≦x,y,a,b,c,d≦10⁹)代表目标位置所在坐标、向上下左右四个方向单次移动的步数。输出描述:
对于每一组测试数据,新起一行。如果小红可以到达目标位置,输出YES;否则,直接输出NO。
解题思路:
本质是求x方向和y方向所需的最大公约数,判断y是否是gcd(a,b)的倍数,且x是否是gcd(c,d)的倍数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int T = scanner.nextInt();
while (T-- > 0) {
long x = scanner.nextLong();
long y = scanner.nextLong();
long a = scanner.nextLong();
long b = scanner.nextLong();
long c = scanner.nextLong();
long d = scanner.nextLong();
// 计算y方向所需的最大公约数
long gcdY = gcd(a, b);
// 计算x方向所需的最大公约数
long gcdX = gcd(c, d);
// 判断y是否是gcd(a,b)的倍数,且x是否是gcd(c,d)的倍数
if (y % gcdY == 0 && x % gcdX == 0) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}
// 欧几里得算法计算最大公约数
private static long gcd(long a, long b) {
while (b != 0) {
long temp = b;
b = a % b;
a = temp;
}
return a;
}
}HJ133 隐匿社交网络
描述:
牛客网有一个名为牛爱网神秘的入口。这天,牛可乐正在策划牛爱网的全新社交活动。
每个人的账号在初始时都会被分配一个权重,第i个账号的权重为wᵢ。对于任意的两个账号i和j,如果权重满足(wᵢ and wⱼ)≧1,那么就会被分配到同一个社交网络。
现在,牛可乐已经为n个账号分配了权重,他想知道,包含账号数量最多的社交网络中,包含多少个账号。
牛爱网的日常维护工作忙坏了牛可乐,请你帮帮他。输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数T(1≦T≦10⁵)代表数据组数,每组测试数据描述如下:
第一行输入一个整数n(1≦n≦10⁵)代表账号数量。
第二行输入n个整数w₁,w₂,…,wₙ(1≦wᵢ≦10¹⁸)代表账号权重。
除此之外,保证单个测试文件的n之和不超过10⁵。输出描述:
对于每组测试数据,新起一行。输出一个整数,代表包含账号数量最多的社交网络中,包含的账号数量。
解题思路:
读取T组测试数据,对于每组数据,读取n和n个权重。
初始化并查集:parent数组和size数组。
初始化first数组,长度为61(因为2⁶⁰大约1e18,所以0到60位),初始值为-1。
遍历每个账号,对于每个账号的权重,遍历0到60位,检查每一位是否为1。
如果该位为1,则进行合并操作。
遍历并查集,找到最大的size,输出最大size
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int T = in.nextInt();
while (T-- > 0) {
int n = in.nextInt();
long[] w = new long[n];
for (int i = 0; i < n; i++) {
w[i] = in.nextLong();
}
// 初始化并查集
int[] parent = new int[n];
int[] size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
// 记录每个二进制位第一次出现的账号索引
int[] first = new int[61];
Arrays.fill(first, -1);
// 处理每个账号
for (int i = 0; i < n; i++) {
for (int j = 0; j <= 60; j++) {
if ((w[i] & (1L << j)) != 0) {
if (first[j] == -1) {
first[j] = i; // 记录该位第一次出现的账号
} else {
// 合并当前账号和该位第一次出现的账号
union(parent, size, i, first[j]);
}
}
}
}
// 找到最大的连通分量
int maxSize = 0;
for (int i = 0; i < n; i++) {
if (parent[i] == i) { // 根节点
maxSize = Math.max(maxSize, size[i]);
}
}
System.out.println(maxSize);
}
}
// 查找根节点(带路径压缩)
public static int find(int[] parent, int x) {
if (parent[x] != x) {
parent[x] = find(parent, parent[x]);
}
return parent[x];
}
// 合并两个集合(按大小合并)
public static void union(int[] parent, int[] size, int x, int y) {
int rootX = find(parent, x);
int rootY = find(parent, y);
// 已经在同一集合
if (rootX == rootY) {
return;
}
// 按大小合并,小树合并到大树
if (size[rootX] < size[rootY]) {
parent[rootX] = rootY;
size[rootY] += size[rootX];
} else {
parent[rootY] = rootX;
size[rootX] += size[rootY];
}
}
}HJ141 小红的二叉树
描述:
小红想知道,深度为n的满二叉树有多少条长度为2的简单路径?由于答案可能很大,请将答案对(10⁹+7)取模后输出。
在本题中,两条简单路径所包含的点集不同时,被视为不同的。例如,路径u−v与路径v−u被视为相同的,因为它们均包含点u与点v。
一棵深度为h的满二叉树由恰好2ʰ−1个节点组成,每一个节点要么是叶子节点,要么有2个儿子,并且全部叶子节点的深度均为h。
简单路径是指这样一条路径,其经过的顶点和边互不相同。输入描述:
在一行上输入一个正整数n(1≦n≦10⁴)代表满二叉树的深度。
输出描述:
输出一个整数,代表深度为n的满二叉树中,长度为2的简单路径的数量。由于答案可能很大,请将答案对(10⁹+7)取模后输出。
解题思路:
当二叉树高度>= 2时,路径总数s = 3 * pow(2, (n - 1)) - 5。另外为防止数值溢出,收集i结果变量需要定为long型,且需要在每一次乘法后 % 1000000007L,最后输出答案即可。
import java.util.*;
public class Main {
static final long MOD = 1000000007L;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
if (n == 1) {
System.out.println(0);
} else {
long res = 1;
for (int i = 0; i < n - 1; i++) {
res *= 2;
res %= MOD;
}
long s = (3 * res) % MOD - 5;
System.out.println(s);
}
}
}HJ147 最大 FST 距离
描述:
给定n个元素,第i个元素具有特征值Ai。定义FST 距离如下:
dist(i,j)=∣i²−j²∣+∣Aᵢ²−Aⱼ²∣
请计算Ai中所有元素对儿中的最大FST距离。输入描述:
第一行输入一个整数n(1≦n≦10⁵)。
第二行输入n个整数A₁,A₂,…,Aₙ(1≦Aᵢ≦10⁹)。输出描述:
输出一个整数,表示最大距离。
解题思路:
FST距离可以视为二维平面上点(索引平方,特征值平方)之间的曼哈顿距离。最大曼哈顿距离等于变换后的坐标(U = i² + Aᵢ² 和 V = i² - Aᵢ²)中最大差值的最大值。计算每个元素的U和V值,然后找出U和V的最大值和最小值。最终结果是U的最大差值(maxU - minU)和V的最大差值(maxV - minV)中的较大值。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
long[] A = new long[n];
for (int i = 0; i < n; i++) {
A[i] = in.nextLong();
}
long minU = Long.MAX_VALUE;
long maxU = Long.MIN_VALUE;
long minV = Long.MAX_VALUE;
long maxV = Long.MIN_VALUE;
for (int i = 0; i < n; i++) {
// 注意索引是从1开始的
long index = i + 1;
long x = index * index;
long y = A[i] * A[i];
long U = x + y;
long V = x - y;
minU = Math.min(minU, U);
maxU = Math.max(maxU, U);
minV = Math.min(minV, V);
maxV = Math.max(maxV, V);
}
// 最大距离是两个差值中的较大者
long maxDist = Math.max(maxU - minU, maxV - minV);
System.out.println(maxDist);
}
}HJ151 模意义下最大子序列和(Easy Version)
描述:
给定一个含有n个正整数的数组a以及一个正整数模数m。你可以任选若干下标递增的元素构成一个子序列(允许选择空序列)。设所选元素之和为S,求S mod m的最大可能值。
输入描述:
第一行输入两个整数n,m(1≦n≦15, 1≦m≦10⁹)。
第二行输入n个整数aᵢ(1≦aᵢ≦10⁹)。输出描述:
输出一个整数,表示S mod m的最大值。
解题思路:
所有可能的子序列对应数组的所有子集。通过遍历所有子集,计算每个子集的元素和,并取模m,可以找到最大值。使用位掩码技术枚举所有子集。对于每个子集,计算其元素和,并更新模m的最大值。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int[] ints = new int[n];
for (int i = 0; i < n; i++) {
ints[i] = in.nextInt();
}
long maxMod = 0;
int total = 1 << n;
for (int mask = 0; mask < total; mask++) {
long sum = 0;
for (int i = 0; i < n; i++) {
if ((mask & (1 << i)) != 0) {
sum += ints[i];
}
}
long modValue = sum % m;
if (modValue > maxMod) {
maxMod = modValue;
}
}
System.out.println(maxMod);
}
}HJ152 取数游戏
描述:
一个N×M的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻8个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。
输入描述:
第一行有一个正整数T(1≦T≦20),表示了有T组数据。
对于每一组数据,第一行有两个正整数N,M(1≦N,M≦6),表示了数字矩阵为N行M列。
接下来N行,每行M个非负整数,描述了这个数字矩阵,满足1≦aᵢ,ⱼ≦10⁵。输出描述:
输出共T行,每行一个非负整数,输出所求得的答案。
解题思路:
需要在网格中选择不相邻的数字(包括八个方向),使得它们的和最大。这是一个典型的在网格上寻找最大权独立集的问题。
从网格的左上角开始,逐个考虑每个格子,对于每个格子有两种选择:
不选择当前格子,直接考虑下一个格子
选择当前格子(如果与已选格子不相邻),然后跳过所有与当前格子相邻的格子
使用递归DFS,并在过程中记录当前已选格子的和。
import java.util.*;
public class Main {
static int N, M;
static int[][] grid;
static int maxSum;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int T = scanner.nextInt();
while (T-- > 0) {
N = scanner.nextInt();
M = scanner.nextInt();
grid = new int[N][M];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
grid[i][j] = scanner.nextInt();
}
}
maxSum = 0;
dfs(0, 0, 0, new boolean[N][M]);
System.out.println(maxSum);
}
}
static void dfs(int i, int j, int currentSum, boolean[][] selected) {
if (i == N) {
// 处理完所有行,更新最大和
if (currentSum > maxSum) {
maxSum = currentSum;
}
return;
}
if (j == M) {
// 处理完当前行,转到下一行
dfs(i + 1, 0, currentSum, selected);
return;
}
// 不选择当前格子
dfs(i, j + 1, currentSum, selected);
// 尝试选择当前格子(如果与已选格子不相邻)
if (canSelect(i, j, selected)) {
// 标记当前格子为已选
selected[i][j] = true;
// 递归处理下一个格子
dfs(i, j + 1, currentSum + grid[i][j], selected);
// 回溯
selected[i][j] = false;
}
}
static boolean canSelect(int i, int j, boolean[][] selected) {
// 检查八个方向是否有已选格子
for (int dx = -1; dx <= 1; dx++) {
for (int dy = -1; dy <= 1; dy++) {
if (dx == 0 && dy == 0) {
continue;
}
int ni = i + dx;
int nj = j + dy;
if (ni >= 0 && ni < N && nj >= 0 && nj < M && selected[ni][nj]) {
return false;
}
}
}
return true;
}
}HJ153 实现字通配符*
描述:
在 Linux Shell 中,通配符`*`代表任意长度(可为0)的字符串。给定:
- 一条模式串`p`(仅包含可见字符及通配符 `*`,无其他元字符);
- 一条目标串`s`;
请输出`s`中所有与`p`匹配的子串的起始位置(从0开始计)及长度。
若不存在匹配,输出`-1 0`。多组匹配按"起始位置升序,长度升序"排序输出。
>`*`可匹配空串;匹配不要求整个`s`,只需匹配其任一连续子串。输入描述:
第一行:模式串`p`(长度不超过20)
第二行:目标串`s`(长度不超过 5×10⁶)
保证输出的总行数不超过5×10⁶。
输出描述:
对每一个匹配子串输出 `匹配起始位置 匹配的长度`(空格分隔)一行;若无匹配输出 `-1 0`。
解题思路:
如果p不是都由*构成,则将p中的*改为.*,否则改为[\\s\\S]*,代表匹配所有字符,然后获取s的所有子字符串,进行匹配,获取匹配的字符串起始位置和长度,放入Set去重,然后打印Set
import java.util.*;
import java.util.regex.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String p = in.nextLine();
if (!"".equals(p.replaceAll("\\*", ""))) {
p = p.replaceAll("\\*", ".*");
} else {
p = "[\\s\\S]*";
}
String s = in.nextLine();
Pattern pattern = Pattern.compile(p);
Matcher matcher1 = pattern.matcher(s);
if (!matcher1.find()) {
System.out.println(-1 + " " + 0);
return;
}
List<String> list = getSubstrings(s);
Set<Result> set = new TreeSet<>();
for (String temp : list) {
Matcher matcher = pattern.matcher(temp);
while (matcher.find()) {
String group = matcher.group();
if ("".equals(group)) {
continue;
}
int index = 0;
while ((index = s.indexOf(group, index)) != -1) {
set.add(new Result(index, group.length()));
index += group.length();
}
}
}
for (Result result : set) {
System.out.println(result.index + " " + result.length);
}
if (set.size() == 0) {
System.out.println(-1 + " " + 0);
}
}
public static List<String> getSubstrings(String str) {
List<String> substrings = new ArrayList<>();
for (int i = 0; i < str.length(); i++) {
for (int j = i + 1; j <= str.length(); j++) {
String substring = str.substring(i, j);
substrings.add(substring);
}
}
return substrings;
}
public static class Result implements Comparable<Result> {
public int index;
public int length;
public Result(int index, int length) {
this.index = index;
this.length = length;
}
@Override
public int compareTo(Result o) {
if (this.index != o.index) {
return this.index - o.index;
} else {
return this.length - o.length;
}
}
}
}HJ154 kotori和素因子
描述:
kotori 拿到n个互不相同的正整数a₁,a₂,…,aₙ。她要从每个ai中选出一个素因子pᵢ,要求所有选出的素因子两两不同,即 pᵢ≠pⱼ(i≠j)。
若无法满足要求输出−1;否则输出所有选出的素因子之和的最小可能值。
输入描述:
第一行输入整数n(1≦n≦10)。
第二行输入n个两两不同的整数aᵢ(2≦aᵢ≦1000)。输出描述:
若存在合法选取方案,输出最小可能和;否则输出−1。
解题思路:
先求所有数字的质因数,然后DFS遍历
index表示当前处理到第几个数,currentSum表示当前已选素因子的和,usedPrime记录已使用的素因子
对于每个数,尝试所有可能的素因子,如果该素因子未被使用,则选择它并继续搜索
使用回溯法确保所有可能性都被探索
import java.util.*;
public class Main {
static int n;
static int[] a;
// 存储每个数的素因子
static List<List<Integer>> primeFactors;
static int minSum = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
// 预处理每个数的素因子
primeFactors = new ArrayList<>();
for (int num : a) {
primeFactors.add(getPrimeFactors(num));
}
// 使用DFS搜索
dfs(0, 0, new HashSet<>());
// 输出结果
if (minSum == Integer.MAX_VALUE) {
System.out.println(-1);
} else {
System.out.println(minSum);
}
}
// DFS搜索所有可能的组合
static void dfs(int index, int currentSum, Set<Integer> usedPrimes) {
// 剪枝:如果当前和已经大于已知最小和,直接返回
if (currentSum >= minSum) {
return;
}
// 所有数都处理完毕,更新最小和
if (index == n) {
minSum = currentSum;
return;
}
// 尝试当前数的每个素因子
for (int prime : primeFactors.get(index)) {
if (!usedPrimes.contains(prime)) {
usedPrimes.add(prime);
dfs(index + 1, currentSum + prime, usedPrimes);
usedPrimes.remove(prime);
}
}
}
// 获取一个数的所有素因子
static List<Integer> getPrimeFactors(int num) {
List<Integer> factors = new ArrayList<>();
int temp = num;
// 分解质因数
for (int i = 2; i * i <= temp; i++) {
if (temp % i == 0) {
factors.add(i);
while (temp % i == 0) {
temp /= i;
}
}
}
// 如果最后剩下的数大于1,说明它本身是质数
if (temp > 1) {
factors.add(temp);
}
return factors;
}
}HJ160 迷宫
描述:
给定一个n×m的迷宫,迷宫由"#"与"."两种字符组成。其中"#"代表障碍物,"."表示空地。迷宫中还有一个起点"S"和一个终点"E",它们都可以视为空地。
由于近期迷宫发生了塌方,导致起点和终点之间可能并不连通。幸运的是,你拥有一种超能力——在迷宫中移动时(移动方向为上、下、左、右四个方向之一),可以在当前位置朝任一方向(上、下、左、右四个方向之一)释放激光。激光能够清除该方向上所有的障碍物,并且这种超能力至多只能使用一次。
现在,你需要判断是否能利用这种超能力成功从起点到达终点。输入描述:
第一行给定两个整数n,m(2≦n,m≦1000),分别表示迷宫的行数和列数。
下面n行,每行m个字符,描述迷宫的具体布局。字符只包含"#"、"."、"S"和"E",并且起点与终点有且仅有一个。输出描述:
能够到达终点输出YES;否则输出NO。
解题思路:
将迷宫变成行列的比较,然后用BFS算法
import java.util.*;
public class Main {
static char[][] grid; // 迷宫网格
static int n, m; // 迷宫的行数和列数
static int startX, startY, endX, endY; // 起点和终点的坐标
static int[][] DIRS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个移动方向:右、左、下、上
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
grid = new char[n][m];
// 读取迷宫数据
for (int i = 0; i < n; i++) {
String line = in.next();
grid[i] = line.toCharArray();
for (int j = 0; j < m; j++) {
if (grid[i][j] == 'S') {
startX = i;
startY = j;
} else if (grid[i][j] == 'E') {
endX = i;
endY = j;
}
}
}
// 从起点开始BFS,获取起点能到达的所有位置
boolean visS[][] = bfs(startX, startY);
// 如果起点能直接到达终点(不使用激光),输出YES
if (visS[endX][endY]) {
System.out.println("YES");
return;
}
// 从终点开始BFS,获取终点能到达的所有位置
boolean visE[][] = bfs(endX, endY);
// 记录起点能到达的行和列
boolean[] row = new boolean[n]; // row[i]为true表示起点能到达第i行
boolean[] col = new boolean[m]; // col[j]为true表示起点能到达第j列
// 遍历整个网格,标记起点能到达的行和列
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (visS[i][j]) {
row[i] = true; // 起点能到达第i行
col[j] = true; // 起点能到达第j列
}
}
}
// 检查是否存在这样的位置:终点能到达,并且与起点能到达的行或列相邻
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visE[i][j]) { // 如果终点不能到达这个位置,跳过
continue;
}
// 检查相邻的行(上下1行范围内)
for (int k = -1; k <= 1; k++) {
int range = i + k; // 检查第i+k行
if (range >= 0 && range < n && row[range]) {
// 如果起点能到达第range行,说明可以使用激光清除障碍物连接
System.out.println("YES");
return;
}
range = j + k; // 检查第j+k列
if (range >= 0 && range < m && col[range]) {
// 如果起点能到达第range列,说明可以使用激光清除障碍物连接
System.out.println("YES");
return;
}
}
}
}
// 如果所有检查都失败,输出NO
System.out.println("NO");
}
/**
* 广度优先搜索,返回从指定起点能到达的所有位置
*
* @param x 起点的行坐标
* @param y 起点的列坐标
* @return 布尔矩阵,vis[i][j]为true表示从起点能到达位置(i,j)
*/
public static boolean[][] bfs(int x, int y) {
boolean[][] vis = new boolean[n][m]; // 访问标记数组
Queue<int[]> queue = new LinkedList<>(); // BFS队列
queue.offer(new int[]{x, y}); // 起点入队
vis[x][y] = true; // 标记起点已访问
while (!queue.isEmpty()) {
int[] cur = queue.poll(); // 取出队首位置
// 尝试四个方向的移动
for (int[] d : DIRS) {
int nxtX = cur[0] + d[0]; // 下一个位置的行坐标
int nxtY = cur[1] + d[1]; // 下一个位置的列坐标
// 检查边界
if (nxtX < 0 || nxtX >= n || nxtY < 0 || nxtY >= m) continue;
// 检查是否是障碍物或已访问
if (grid[nxtX][nxtY] == '#' || vis[nxtX][nxtY] == true) continue;
// 新位置入队并标记已访问
queue.offer(new int[]{nxtX, nxtY});
vis[nxtX][nxtY] = true;
}
}
return vis;
}
}HJ161 走一个大整数迷宫
描述:
给定一个n×m的矩阵迷宫,其中第i行第j列的格子权值为
LH 起始位于(1,1),出口位于(n,m)。迷宫配有一个计数器,初始值为c1,1。在任意时刻,若计数器的值满足counter≡0(mod(p−1)),且 LH 身处出口(n,m),大门即刻打开,LH 得以逃离。
每经过1秒,LH 必须向上、下、左、右四个方向中的某一方向移动一步(不得停留,也不得走出迷宫)。假设 LH 从(i,j)移动到(i′,j′),则计数器会累加cᵢ′,ⱼ′。
请计算 LH 最快需要多少秒才能逃离;若无论如何都无法逃离,则输出−1。输入描述:
输入共三部分:
- 第一行输入三个整数n,m,p(1≦n,m≦10;2≦p≦10⁴);
- 接下来n行,每行m个整数,构成矩阵aᵢ,ⱼ;
- 再接下来n行,每行m个整数,构成矩阵bi,j,范围均为0≦aᵢ,ⱼ,bᵢ,ⱼ≦10⁶。
输出描述:
输出一个整数,代表最短逃离时间;若无法逃离,输出−1。
解题思路:
利用模运算性质pk ≡ 1 (mod p−1),将复杂的指数运算简化为直接使用ai,j模p−1的值。使用三维状态 (x, y, s),其中:(x, y)表示当前位置,s表示当前路径和模p−1的值。从起点开始,每次向四个方向扩展,更新状态和最短时间,直到找到终点且满足模条件的状态。
static int n, m, p; // 迷宫的行数n,列数m,参数p
static int[][] a; // 矩阵a,存储每个格子的a[i][j]值
static int[][] b; // 矩阵b,题目需要读入但实际上在计算中不会使用
static int[] dx = {0, 0, 1, -1}; // 四个移动方向:右、左、下、上
static int[] dy = {1, -1, 0, 0};
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 读取输入的基本参数
n = in.nextInt();
m = in.nextInt();
p = in.nextInt();
// 初始化矩阵a和b
a = new int[n][m];
b = new int[n][m];
// 读取矩阵a的值
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = in.nextInt();
}
}
// 读取矩阵b的值(虽然读入,但在后续计算中不会使用)
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
b[i][j] = in.nextInt();
}
}
// BFS搜索最短路径
int mod = p - 1; // 模数,根据题目要求counter ≡ 0 (mod p-1)
// dist[x][y][s] 表示到达位置(x,y)且当前和模mod等于s的最短时间
// 初始值为-1表示该状态尚未访问
int[][][] dist = new int[n][m][mod];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
Arrays.fill(dist[i][j], -1);
}
}
// 初始状态:在起点(0,0),初始和为a[0][0] mod (p-1),时间为0
int startSum = a[0][0] % mod;
dist[0][0][startSum] = 0;
// 使用BFS队列进行状态扩展
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{0, 0, startSum}); // 状态格式: [x坐标, y坐标, 当前和模mod的值]
while (!queue.isEmpty()) {
int[] cur = queue.poll();
int x = cur[0], y = cur[1], s = cur[2]; // 当前位置和当前和
int time = dist[x][y][s]; // 到达当前状态的时间
// 如果到达终点(n-1, m-1)且和模mod为0,找到解
if (x == n - 1 && y == m - 1 && s == 0) {
System.out.println(time);
return;
}
// 尝试四个方向的移动
for (int d = 0; d < 4; d++) {
int nx = x + dx[d], ny = y + dy[d]; // 新位置坐标
// 检查新位置是否在迷宫范围内
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
// 计算移动到新位置后的和(模mod)
int ns = (s + a[nx][ny]) % mod;
// 如果这个新状态还没有被访问过
if (dist[nx][ny][ns] == -1) {
// 记录到达新状态的最短时间
dist[nx][ny][ns] = time + 1;
// 将新状态加入队列
queue.offer(new int[]{nx, ny, ns});
}
}
}
// 如果BFS结束都没有找到解,输出-1
System.out.println(-1);
}HJ162 ACM中的AC题
描述:
众所周知,出题人没玩过《双人成行》,于是给出了如下经典二人协作版迷宫问题。孤岛被划分为n×m个方格,按行从上到下、列从左到右编号为(1,1)至(n,m)。地图上的地形分为三种:
- 平地(`.`)——可以自由经过;
- 陷阱(`#`)——踩上去立即死亡;
- 传送门(`@`)——一旦进入便会立刻离开孤岛。
你与来自平行时空的另一个"你"最初同时位于坐标(x,y) 的同一块平地。两人每次必须同时行动,且朝相反方向各移动一步,即:
- 如果你选择向上,则另一个你必须向下;
- 如果你选择向左,则另一个你必须向右,依此类推。
在任何时刻,若有人走出边界或踏入陷阱,游戏立即失败;若有人到达传送门,则他会立刻离开并不再返回,之后剩下的那个人可以单独自由移动(不再受"相反方向"限制)。
请判断是否存在一条合法的移动序列,使得两个人都能成功离开孤岛;若存在,请输出最短所需步数,否则输出−1。输入描述:
输入包含n+1行:
- 第一行输入四个整数n,m,x,y(1≦n,m≦2×10³; 1≦x≦n; 1≦y≦m);
- 接下来n行,第i行输入一个长度为m的字符串sᵢ,仅由`.`、`#`、`@`组成,描述第i行的地形。
保证起点(x,y)处为平地。
输出描述:
若存在可行方案,输出最短移动步数;否则输出−1。
解题思路:
由于两人始终朝相反方向移动,他们的位置保持中心对称:如果A在位置(x1, y1),那么B一定在(2*x0 - x1, 2*y0 - y1),其中(x0, y0)是初始位置,这意味着我们只需要跟踪其中一个人的位置,另一个人的位置可以通过计算得到。
使用两个访问数组避免重复搜索:vis2[x][y]:记录双人阶段是否访问过位置(x,y),vis1[x][y]:记录单人阶段是否访问过位置(x,y)
从初始状态(x0, y0, 0)开始BFS,根据当前阶段选择移动规则:双人阶段:检查对称移动的合法性,单人阶段:自由移动。
遇到传送门时进行阶段转换或直接结束,找到最短路径或确定无解
static int n, m, x0, y0; // 网格行数n,列数m,初始位置(x0,y0)
static char[][] grid; // 网格地图,存储地形信息
static boolean[][] vis1; // 单人阶段访问标记数组
static boolean[][] vis2; // 双人阶段访问标记数组
static int[] dx = {0, 0, 1, -1}; // 四个移动方向:右、左、下、上
static int[] dy = {1, -1, 0, 0};
// BFS状态类,记录当前位置、阶段和步数
static class State {
int x, y; // 当前坐标
int phase; // 阶段:0-双人阶段,1-单人阶段
int steps; // 已走步数
State(int x, int y, int phase, int steps) {
this.x = x;
this.y = y;
this.phase = phase;
this.steps = steps;
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 读取输入参数
n = in.nextInt();
m = in.nextInt();
x0 = in.nextInt();
y0 = in.nextInt();
x0--;
y0--; // 转换为0-based坐标
// 读取网格地图
grid = new char[n][m];
for (int i = 0; i < n; i++) {
grid[i] = in.next().toCharArray();
}
// 初始化访问标记数组
vis1 = new boolean[n][m]; // 单人阶段访问标记
vis2 = new boolean[n][m]; // 双人阶段访问标记
// BFS队列
Queue<State> queue = new LinkedList<>();
// 初始状态:双人阶段,在起点位置,步数为0
vis2[x0][y0] = true;
queue.offer(new State(x0, y0, 0, 0));
// BFS主循环
while (!queue.isEmpty()) {
State cur = queue.poll();
int cx = cur.x, cy = cur.y, phase = cur.phase, steps = cur.steps;
if (phase == 0) {
// 双人阶段:两人都在场,必须朝相反方向移动
for (int d = 0; d < 4; d++) {
// A的新位置
int nx1 = cx + dx[d], ny1 = cy + dy[d];
// B的新位置(根据对称性计算)
int nx2 = 2 * x0 - cx - dx[d], ny2 = 2 * y0 - cy - dy[d];
// 检查A的新位置是否合法(在边界内且不是陷阱)
if (nx1 < 0 || nx1 >= n || ny1 < 0 || ny1 >= m ||
grid[nx1][ny1] == '#') continue;
// 检查B的新位置是否合法
if (nx2 < 0 || nx2 >= n || ny2 < 0 || ny2 >= m ||
grid[nx2][ny2] == '#') continue;
// 检查是否到达传送门
boolean p1_at = (grid[nx1][ny1] == '@');
boolean p2_at = (grid[nx2][ny2] == '@');
if (p1_at && p2_at) {
// 情况1:两人同时到达传送门,游戏结束
System.out.println(steps + 1);
return;
} else if (p1_at) {
// 情况2:A到达传送门,B留下进入单人阶段
if (!vis1[nx2][ny2]) {
vis1[nx2][ny2] = true;
queue.offer(new State(nx2, ny2, 1, steps + 1));
}
} else if (p2_at) {
// 情况3:B到达传送门,A留下进入单人阶段
if (!vis1[nx1][ny1]) {
vis1[nx1][ny1] = true;
queue.offer(new State(nx1, ny1, 1, steps + 1));
}
} else {
// 情况4:两人都移动到平地,继续双人阶段
if (!vis2[nx1][ny1]) {
vis2[nx1][ny1] = true;
queue.offer(new State(nx1, ny1, 0, steps + 1));
}
}
}
} else {
// 单人阶段:只剩一人,可以自由移动
for (int d = 0; d < 4; d++) {
int nx = cx + dx[d], ny = cy + dy[d];
// 检查新位置是否合法
if (nx < 0 || nx >= n || ny < 0 || ny >= m || grid[nx][ny] == '#') continue;
// 如果到达传送门,游戏结束
if (grid[nx][ny] == '@') {
System.out.println(steps + 1);
return;
}
// 移动到平地,继续单人阶段
if (!vis1[nx][ny]) {
vis1[nx][ny] = true;
queue.offer(new State(nx, ny, 1, steps + 1));
}
}
}
}
// BFS结束仍未找到解,输出-1
System.out.println(-1);
}HJ163 时津风的资源收集
描述:
时津风曾沉迷于页游Kancolle。在游戏中,有一项日常任务需要玩家使用油、弹药、钢材、铝这4种资源来开发装备。
现给定目标资源量a,b,c,d,时津风进入开发界面时4种资源均为10单位。她可以对单一资源执行以下任意一种操作(资源总量始终保持在区间[10,300]):
- 将该资源±1;
- 将该资源±10;
- 将该资源±100;
- 直接将该资源设为上限300;
- 直接将该资源设为下限10。
在保证所有资源始终处于合法范围的前提下,求使四种资源同时恰好达到(a,b,c,d)所需的最少操作次数。
输入描述:
第一行输入整数T(1≦T≦10⁵)—— 测试组数。
接下来T行,每行输入4个整数a,b,c,d(10≦a,b,c,d≦300)。输出描述:
对每组数据输出一个整数,表示最少操作次数。
解题思路:
4种资源的操作相互独立,总操作次数=各种资源操作次数之和,由于目标值范围固定(10~300),可以预先计算从10到所有可能值的最少操作次数。
从当前值可以通过8种操作得到新值:+1, -1, +10, -10, +100, -100, 到300, 到10,对于每组测试数据(a,b,c,d),直接查表
import java.util.*;
public class Main {
// dist[x] 表示从初始值10到目标值x所需的最少操作次数
static int[] dist = new int[301]; // 索引范围10~300
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 预处理:计算从10到所有可能目标值的最少操作次数
precompute();
int T = in.nextInt();
StringBuilder sb = new StringBuilder();
while (T-- > 0) {
int a = in.nextInt();
int b = in.nextInt();
int c = in.nextInt();
int d = in.nextInt();
// 总操作次数 = 四种资源各自操作次数的和
int ans = dist[a] + dist[b] + dist[c] + dist[d];
sb.append(ans).append('\n');
}
System.out.print(sb);
}
/**
* 预处理函数:使用BFS计算从10到所有可能值(10~300)的最少操作次数
*/
static void precompute() {
Arrays.fill(dist, -1); // -1表示尚未访问
Queue<Integer> q = new LinkedList<>();
dist[10] = 0; // 起点10,操作次数为0
q.offer(10); // 将起点加入队列
while (!q.isEmpty()) {
int cur = q.poll(); // 当前处理的数值
// 尝试所有可能的操作:
// 操作1:当前值 ±1
tryMove(cur, cur + 1, dist, q);
tryMove(cur, cur - 1, dist, q);
// 操作2:当前值 ±10
tryMove(cur, cur + 10, dist, q);
tryMove(cur, cur - 10, dist, q);
// 操作3:当前值 ±100
tryMove(cur, cur + 100, dist, q);
tryMove(cur, cur - 100, dist, q);
// 操作4:直接设为上限300
tryMove(cur, 300, dist, q);
// 操作5:直接设为下限10
tryMove(cur, 10, dist, q);
}
}
/**
* 尝试从当前值cur移动到next值,如果合法且未访问过,则更新距离并加入队列
* @param cur 当前值
* @param next 下一个值
* @param dist 距离数组
* @param q BFS队列
*/
static void tryMove(int cur, int next, int[] dist, Queue<Integer> q) {
// 检查next值是否在合法范围内[10,300]且未被访问过
if (next >= 10 && next <= 300 && dist[next] == -1) {
// 更新操作次数:当前值的操作次数+1
dist[next] = dist[cur] + 1;
// 将新值加入队列继续BFS
q.offer(next);
}
}
}HJ164 太阳系DISCO
描述:
在一个平行世界的太阳系中,所有行星恰好构成一个长度为n的环,按顺时针依次编号为1,2,…,n。相邻两颗行星间距离相等,且保证n为偶数。
你位于编号为a的行星,目标是到达编号为b的行星。你可以执行以下三种操作,每次操作均消耗1个单位时间:
- 顺时针移动x颗行星;
- 逆时针移动y颗行星;
- 发动一次传送技能(最多可使用k次),将你顺时针移动n/2颗行星,即跳到正对面的那颗行星。
请你计算,从a行星移动到b行星的最少时间;若无论如何都无法到达,则输出−1。
输入描述:
在一行上输入6个整数n,k,a,b,x,y,含义分别为:
- n(2≦n≦2×10⁵)——行星数量,且n为偶数;
- k(0≦k≦2×10⁵)——技能可使用的最大次数;
- a,b(1≦a,b≦n)——起点与终点的编号;
- x,y(1≦x,y≦n)——每次普通移动的距离。
输出描述:
输出一个整数,表示最少所需时间;若无法到达,则输出−1。
解题思路:
实际上只有两种不同的起点位置:起点a(传送偶数次),起点a + n/2(传送奇数次)
将原问题分解为:计算普通移动的最少时间:使用BFS在模n环上搜索最短路径,枚举传送次数:分别考虑偶数和奇数传送次数的情况,合并计算总时间:总时间 = 普通移动时间 + 传送次数
状态:当前余数 r = (当前位置 - 起点) mod n
初始状态:r = 0(起点)
目标状态:r = (目标位置 - 起点) mod n
状态转移:顺时针移动x:r → (r + x) mod n,逆时针移动y:r → (r - y + n) mod n
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); // 行星数量(偶数)
int k = in.nextInt(); // 最大传送次数
int a = in.nextInt(); // 起点行星编号
int b = in.nextInt(); // 终点行星编号
int x = in.nextInt(); // 顺时针移动步长
int y = in.nextInt(); // 逆时针移动步长
// 两种不同的起点类型:
// start1: 传送偶数次后的位置(包括0次),即起点a
int start1 = a;
// start2: 传送奇数次后的位置,即起点a的对侧位置
int start2 = (a - 1 + n / 2) % n + 1; // 1-based坐标转换
// 使用BFS计算从每种起点到终点的最少普通移动次数(不使用传送)
int dist1 = bfs(n, start1, b, x, y); // 从起点a到b
int dist2 = bfs(n, start2, b, x, y); // 从起点a的对侧到b
long ans = Long.MAX_VALUE; // 初始化答案为最大值
// 情况1:使用偶数次传送(0,2,4,...次)
for (int t = 0; 2 * t <= k; t++) {
if (dist1 != -1) { // 如果从起点a可以到达终点b
// 总时间 = 普通移动时间 + 传送次数
ans = Math.min(ans, dist1 + 2L * t);
}
}
// 情况2:使用奇数次传送(1,3,5,...次)
for (int t = 0; 2 * t + 1 <= k; t++) {
if (dist2 != -1) { // 如果从起点a的对侧可以到达终点b
// 总时间 = 普通移动时间 + 传送次数
ans = Math.min(ans, dist2 + 2L * t + 1);
}
}
// 输出结果:如果找到了可行解则输出最少时间,否则输出-1
System.out.println(ans == Long.MAX_VALUE ? -1 : ans);
}
/**
* 使用BFS在模n意义下计算从起点到终点的最少普通移动次数
* @param n 行星总数
* @param start 起点行星编号
* @param target 终点行星编号
* @param x 顺时针移动步长
* @param y 逆时针移动步长
* @return 最少移动次数,如果无法到达返回-1
*/
static int bfs(int n, int start, int target, int x, int y) {
// 计算起点到终点的模n差值(环上的相对位置)
int diff = (target - start + n) % n;
// 如果起点和终点相同,不需要移动
if (diff == 0) return 0;
// dist数组记录从起点(余数0)到每个余数的最少步数
int[] dist = new int[n];
Arrays.fill(dist, -1); // -1表示未访问
Queue<Integer> queue = new LinkedList<>();
// 初始状态:余数为0(即起点位置),步数为0
dist[0] = 0;
queue.offer(0);
while (!queue.isEmpty()) {
int cur = queue.poll(); // 当前余数
// 操作1:顺时针移动x步
int next1 = (cur + x) % n; // 计算新余数
if (dist[next1] == -1) { // 如果新状态未访问
dist[next1] = dist[cur] + 1; // 更新步数
if (next1 == diff) { // 如果到达目标余数
return dist[next1]; // 返回最少步数
}
queue.offer(next1); // 新状态加入队列
}
// 操作2:逆时针移动y步
int next2 = (cur - y + n) % n; // 计算新余数(+n保证非负)
if (dist[next2] == -1) { // 如果新状态未访问
dist[next2] = dist[cur] + 1; // 更新步数
if (next2 == diff) { // 如果到达目标余数
return dist[next2]; // 返回最少步数
}
queue.offer(next2); // 新状态加入队列
}
}
// BFS结束仍未到达目标,返回-1表示无法到达
return -1;
}
}HJ176 【模板】滑动窗口
描述:
给定一个长度为n的整数数组a和一个窗口大小k(1≦k≦n)。滑动窗口从左到右移动,每次右移一位(窗口覆盖下标[i,i+k−1])。对于数组的每一个窗口位置,求出窗口内元素的最大值。
输入描述:
第一行输入两个整数n,k(1≦k≦n≦2×10⁵)。
第二行输入n个整数a₁,a₂,…,aₙ,元素范围1≦aᵢ≦10⁹。输出描述:
输出共n−k+1个整数,为每个滑动窗口的最大值,数之间以单个空格分隔。
解题思路:
单调递减性质:队列中的下标对应的元素值是单调递减的
队首元素:始终是当前窗口的最大值对应的下标
队尾插入:新元素从队尾插入,保持队列的单调性
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); // 数组长度
int k = in.nextInt(); // 窗口大小
int[] a = new int[n]; // 存储数组元素
Deque<Integer> dq = new LinkedList<>(); // 双端队列,存储数组下标(维护单调递减序列)
StringBuilder sb = new StringBuilder(); // 用于构建输出结果
// 读取数组元素
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
// 滑动窗口处理
for (int i = 0; i < n; i++) {
// 步骤1:维护队列的单调递减性
// 从队列尾部开始,移除所有小于等于当前元素的下标
// 因为这些元素不可能是当前或未来窗口的最大值
while (!dq.isEmpty() && a[i] >= a[dq.peekLast()]) {
dq.pollLast(); // 移除队尾元素
}
// 步骤2:将当前元素下标加入队列尾部
dq.offerLast(i);
// 步骤3:维护窗口范围,移除不在当前窗口内的队首元素
// 检查队首元素是否已经超出窗口左边界(i - k)
while (!dq.isEmpty() && i - dq.peekFirst() >= k) {
dq.pollFirst(); // 移除队首元素
}
// 步骤4:当窗口形成后(i >= k-1),输出当前窗口最大值
// 队列头部始终是当前窗口最大值的下标
if (i >= k - 1) {
sb.append(a[dq.peekFirst()]).append(" ");
}
}
// 输出所有窗口的最大值
System.out.println(sb.toString().trim());
}
}HJ178 【模板】双指针
描述:
对于给定的长度为n的数组{a₁,a₂,…,aₙ},找出最长的区间,满足区间中元素两两不同。
如果有多个这样的区间,依次输出它们。
输入描述:
第一行输入一个整数n(1≦n≦2×10⁵)代表数组中的元素数量。
第二行输入n个整数a₁,a₂,…,aₙ(0≦ai≦n)代表初始数组。
输出描述:
第一行输出一个整数m(1≦m≦n)代表满足条件的区间数量。
此后m行,每行输出两个整数l,r(1≦l≦r≦n)代表满足条件的区间。本题没有SPJ,请按照l递增的顺序输出。
解题思路:
如果当前元素在窗口内出现过(即上次出现位置≥left),将左边界移动到重复元素的下一个位置,保证窗口内无重复
发现更长区间:清空之前结果,只保留新的最长区间,发现等长区间:添加到结果列表中
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); // 读取数组长度
int[] a = new int[n]; // 存储数组元素
// 读取数组元素
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
// lastSeen 数组记录每个元素最近一次出现的下标
// 数组大小为 n+1 是因为元素范围是 0~n
int[] lastSeen = new int[n + 1];
Arrays.fill(lastSeen, -1); // 初始化为-1,表示元素尚未出现过
int left = 0; // 滑动窗口的左边界
int maxLen = 0; // 记录当前找到的最长无重复区间长度
List<int[]> intervals = new ArrayList<>(); // 存储所有最长无重复区间
// 使用滑动窗口(双指针)遍历数组
for (int right = 0; right < n; right++) {
// 如果当前元素a[right]在窗口[left, right)内已经出现过
// 需要移动左边界来保证窗口内无重复元素
if (lastSeen[a[right]] >= left) {
left = lastSeen[a[right]] + 1; // 左边界移动到重复元素的下一个位置
}
// 更新当前元素最近出现的位置
lastSeen[a[right]] = right;
// 计算当前窗口的长度
int len = right - left + 1;
if (len > maxLen) {
// 找到更长的无重复区间,更新最大长度并重置结果列表
maxLen = len;
intervals.clear(); // 清空之前存储的较短区间
intervals.add(new int[]{left, right}); // 添加新区间
} else if (len == maxLen) {
// 找到与当前最大长度相同的区间,添加到结果列表
intervals.add(new int[]{left, right});
}
}
// 输出结果
// 第一行:输出最长无重复区间的数量
System.out.println(intervals.size());
// 后续每行:输出每个区间的起始和结束位置(转换为1-based索引)
for (int[] interval : intervals) {
// 注意:题目要求输出1-based索引,所以需要+1
System.out.println((interval[0] + 1) + " " + (interval[1] + 1));
}
}
}HJ179 小苯的IDE括号问题(easy)
描述:
在一款智能代码编辑器中,光标用字符I表示。初始时给出一个只包含字符(、)、I的括号串,其中恰好出现一次I作为光标位置。编辑器支持下列两种删除操作:
1. backspace:
- 若光标左侧字符为`(`,且光标右侧紧跟字符为`)`,编辑器会一次性删除这对括号;
- 否则,若光标左侧仍有字符,则仅删除光标左侧一个字符;若左侧为空则无效
2. delete:
- 若光标右侧存在字符,则删除光标右侧第一个字符;否则无效果。
给定初始括号串以及k次操作序列(每次为backspace或delete),请输出全部操作执行完毕后的最终字符串。
输入描述:
第一行输入两个整数n,k(1≦k≦n≦2×10⁵)——初始字符串长度及操作次数。
第二行输入长度为n的字符串s,仅包含`(`, `)`与`I`,其中I恰好出现一次。
接下来k行,每行输入一个操作类型:backspace或delete。输出描述:
输出一行字符串,表示所有操作结束后的括号串。
解题思路:
根据index和前后字符,修改字符数组,然后遍历
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
String str = in.next();
int index = str.indexOf('I');
char[] chars = str.toCharArray();
int j = index, k = index;
for (int i = 0; i < m; i++) {
String commend = in.next();
if (commend.equals("backspace")) {
if (j != 0 && k + 1 != n && chars[j - 1] == '(' && chars[k + 1] == ')') {
chars[j - 1] = 'e';
chars[k + 1] = 'e';
j--;
k++;
} else if (j != 0) {
chars[j - 1] = 'e';
j--;
}
}
if (commend.equals("delete")) {
if (k + 1 != n) {
chars[k + 1] = 'e';
k++;
}
}
}
for (int i = 0; i < n; i++) {
if (chars[i] != 'e') {
System.out.print(chars[i]);
}
}
}
}HJ180 游游的最长稳定子数组
描述:
定义一个数组被称为稳定,当且仅当对于数组中任意相邻元素
,都有
。
给定长度为n的整数数组a,请你求出其最长稳定连续子数组的长度。输入描述:
第一行输入一个整数n(1≦n≦10⁵)——数组长度。
第二行输入n个整数a₁,a₂,…,aₙ(1≦aᵢ≦10⁹)——数组元素。输出描述:
输出一个整数,表示最长稳定连续子数组的长度。
解题思路:
遍历获取符合条件的最长子数组的长度
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
if (n <= 1) {
System.out.println(n);
return;
}
int maxLen = 1;
int currentLen = 1;
for (int i = 1; i < n; i++) {
if (Math.abs(arr[i] - arr[i - 1]) <= 1) {
currentLen++;
maxLen = Math.max(maxLen, currentLen);
} else {
currentLen = 1;
}
}
System.out.println(maxLen);
}
}HJ181 相差不超过k的最多数
描述:
给定一个包含n个正整数的数组a₁,a₂,…,aₙ。你需要从中选择若干个数(可以全部也可以一个都不选),使得在所选集合中任意两数的差的绝对值均不超过给定整数k。
请输出能够选出的元素个数的最大值。
【名词解释】
若选出的元素集合为S,则要求max(S)−min(S)≦k。输入描述:
第一行输入两个整数n,k(1≦n≦2×10⁵, 1≦k≦10⁹)。
第二行输入n个整数a₁,a₂,…,aₙ(1≦ai≦10⁹)。输出描述:
输出一个整数,表示满足条件的最多可选元素数量。
解题思路:
对数组排序,然后双重循环,遍历数组
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = in.nextInt();
}
long res = 0;
Arrays.sort(arr);
int left = 0;
for (int i = 0; i < n; i++) {
while (left < i && arr[i] - arr[left] > k) {
left++;
}
res = Math.max(res, i - left + 1);
}
System.out.println(res);
}
}HJ182 画展布置
描述:
展厅共有N幅画作,其艺术价值为整数A₁,A₂,…,AN。策展人需选出其中M幅依次摆放。设选出后排成一列的价值为B₁,…,BM,定义一个画展的不和谐度L满足:
请最小化L并输出其最小可能值。输入描述:
第一行输入两个整数N,M(2≦M≦N≦10⁵)。
第二行输入N个整数A₁…AN(1≦Aᵢ≦10⁵)。输出描述:
输出一个整数,表示最小化后的L值。
解题思路:
其本质,就是对数组内元素的平方排序,然后比较相隔m-1的差的最小值
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
long[] ints = new long[n];
for (int i = 0; i < n; i++) {
ints[i] = in.nextLong();
}
long[] sqrts = new long[n];
for (int i = 0; i < n; i++) {
sqrts[i] = ints[i] * ints[i];
}
Arrays.sort(sqrts);
Long min = Long.MAX_VALUE;
for (int i = 0; i <= n - m; i++) {
min = Math.min(min, Math.abs(sqrts[i] - sqrts[i + m - 1]));
}
System.out.println(min);
}
}




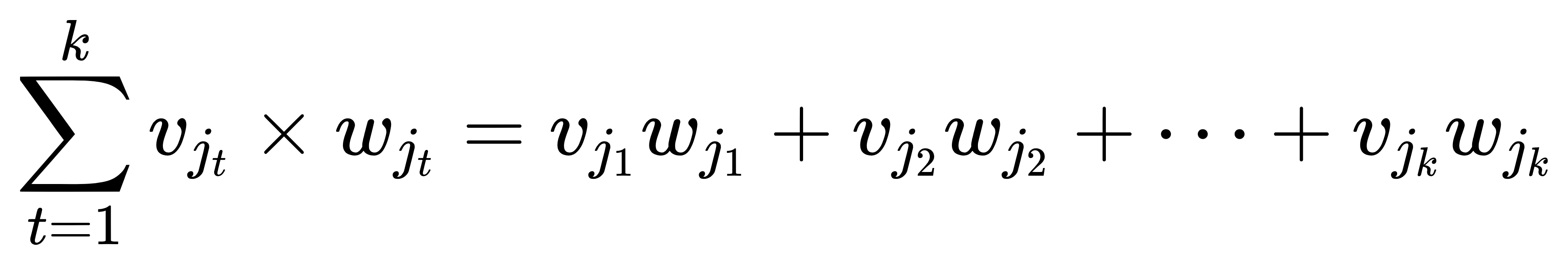




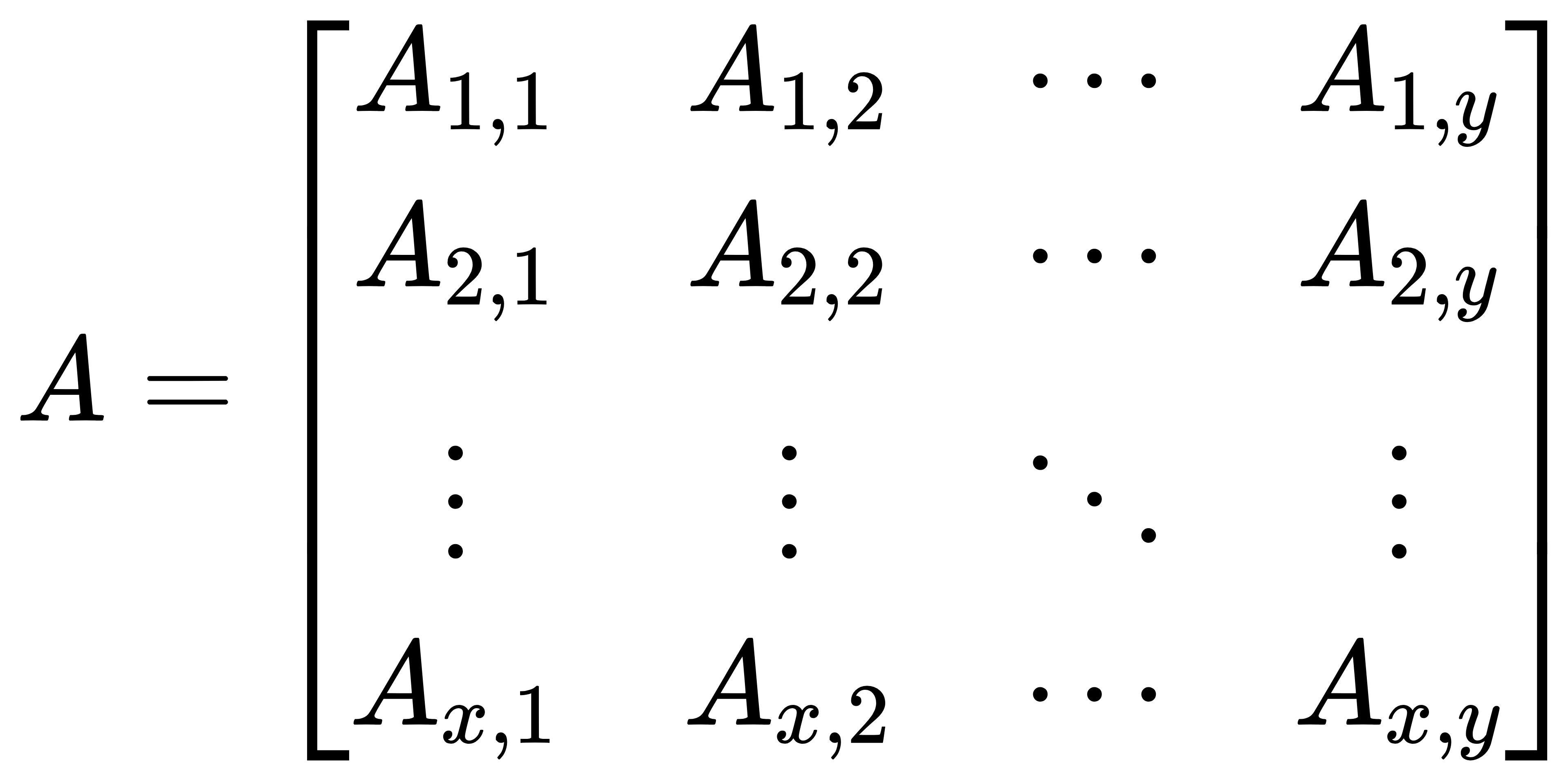
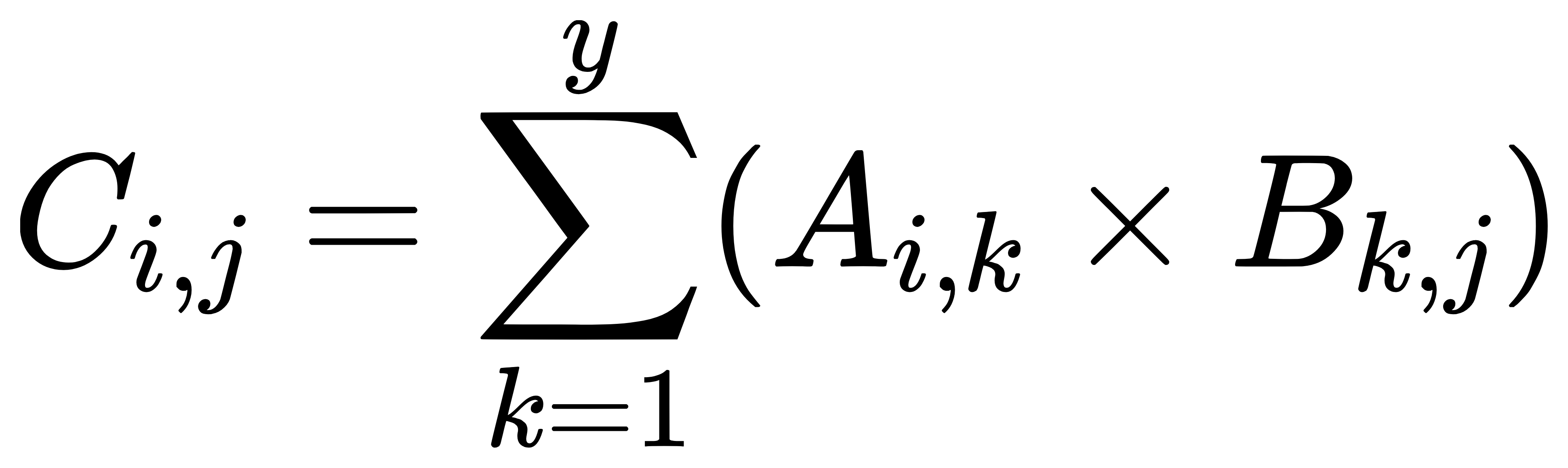
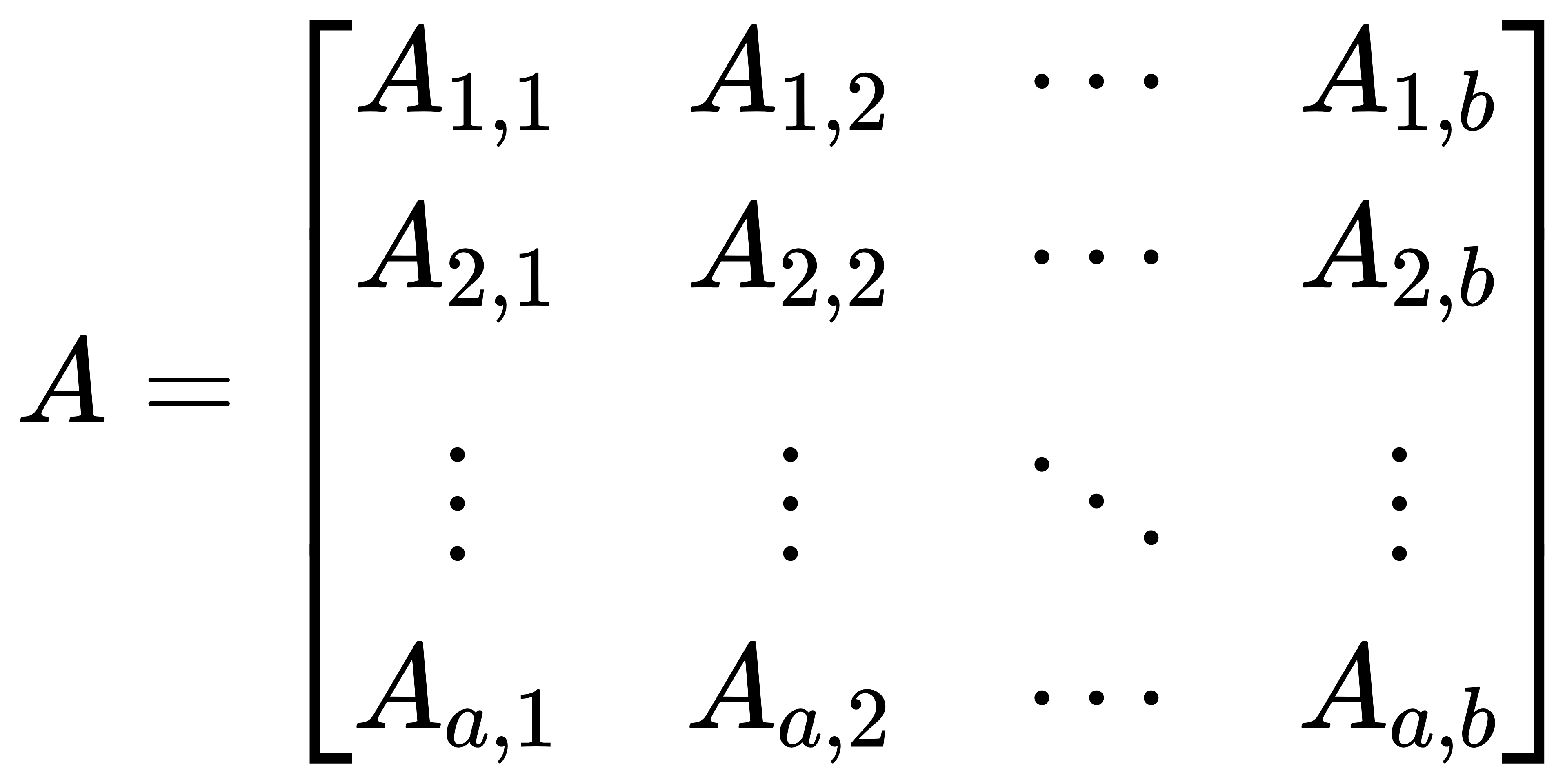
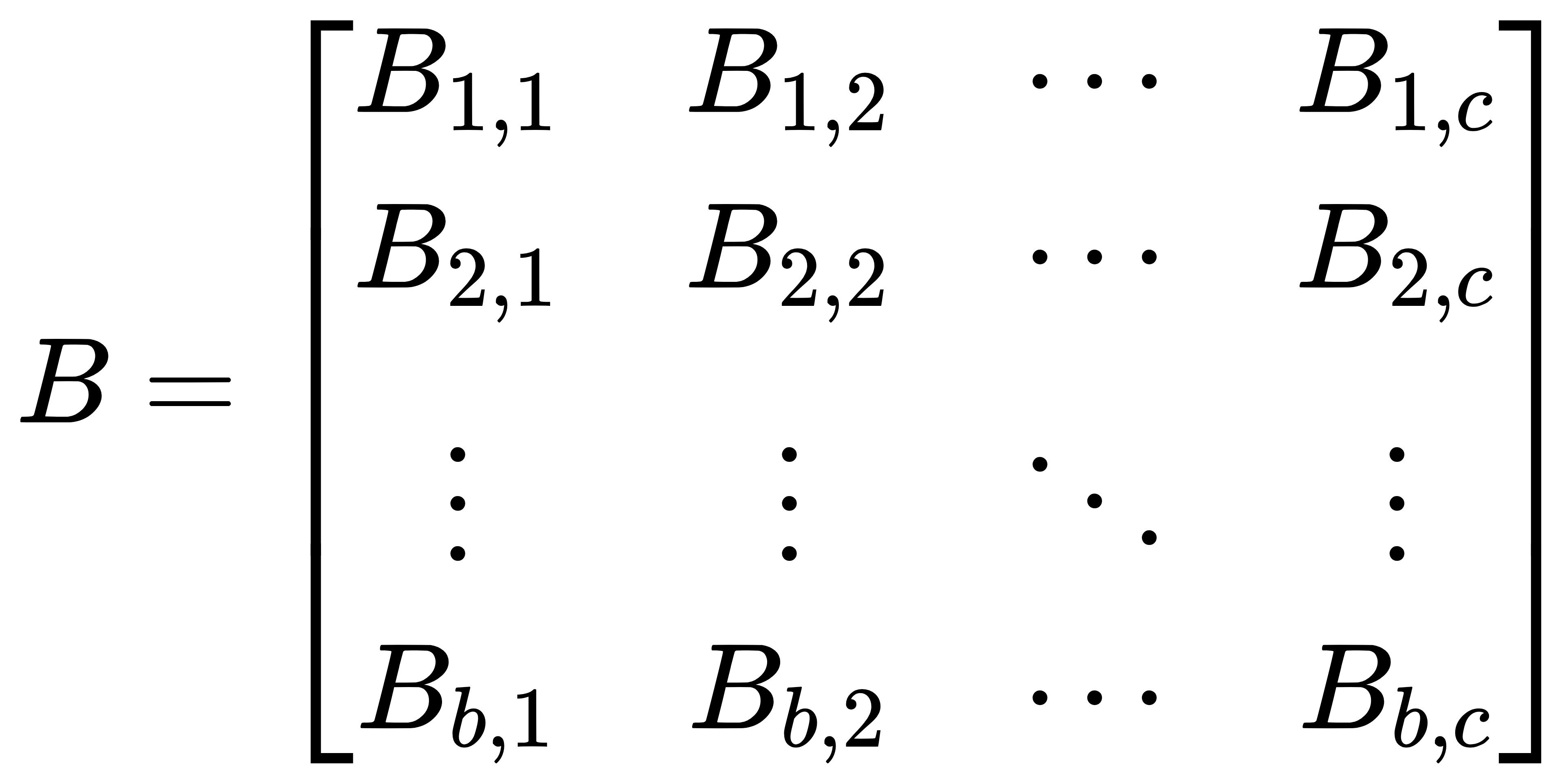
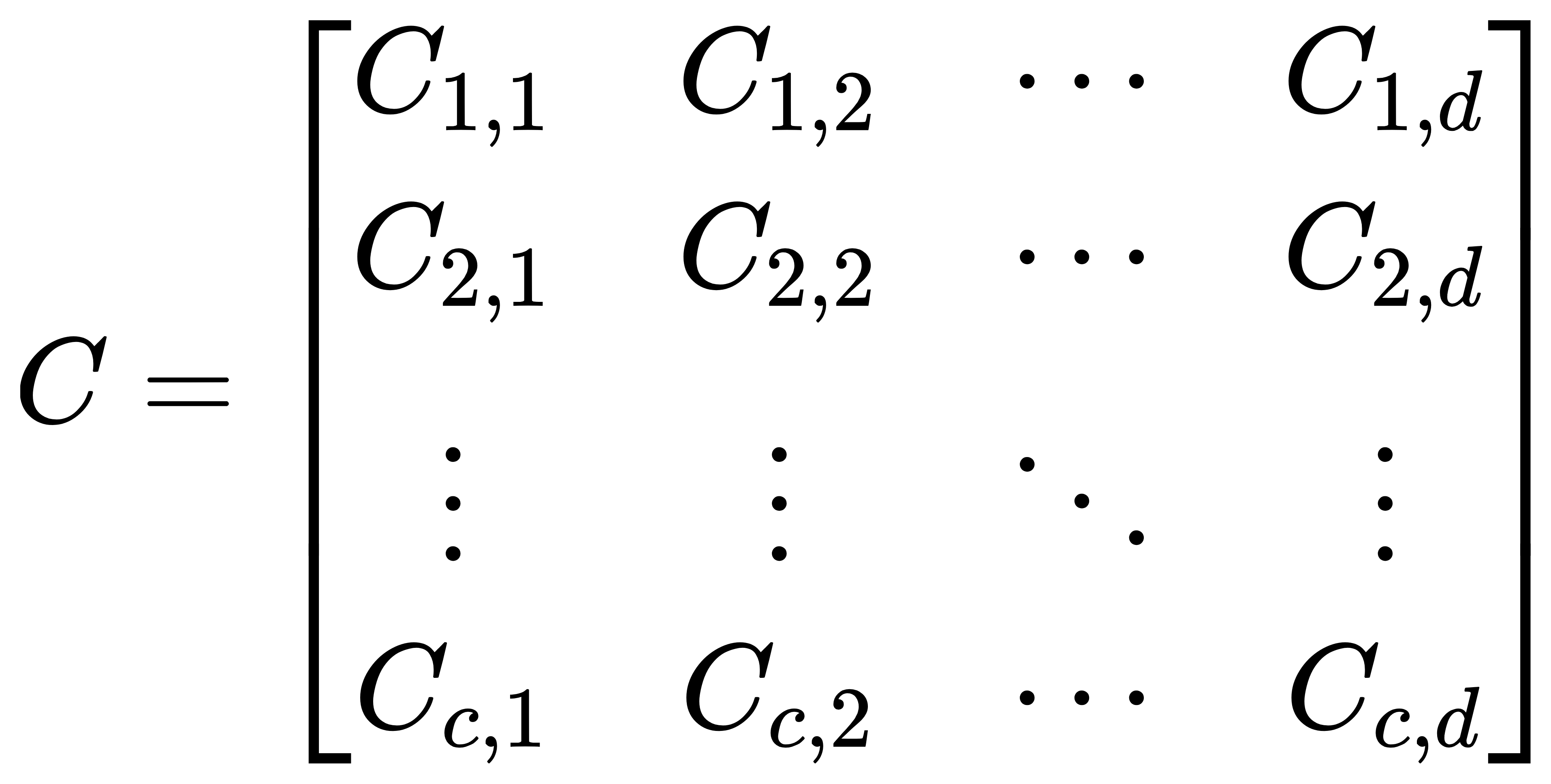
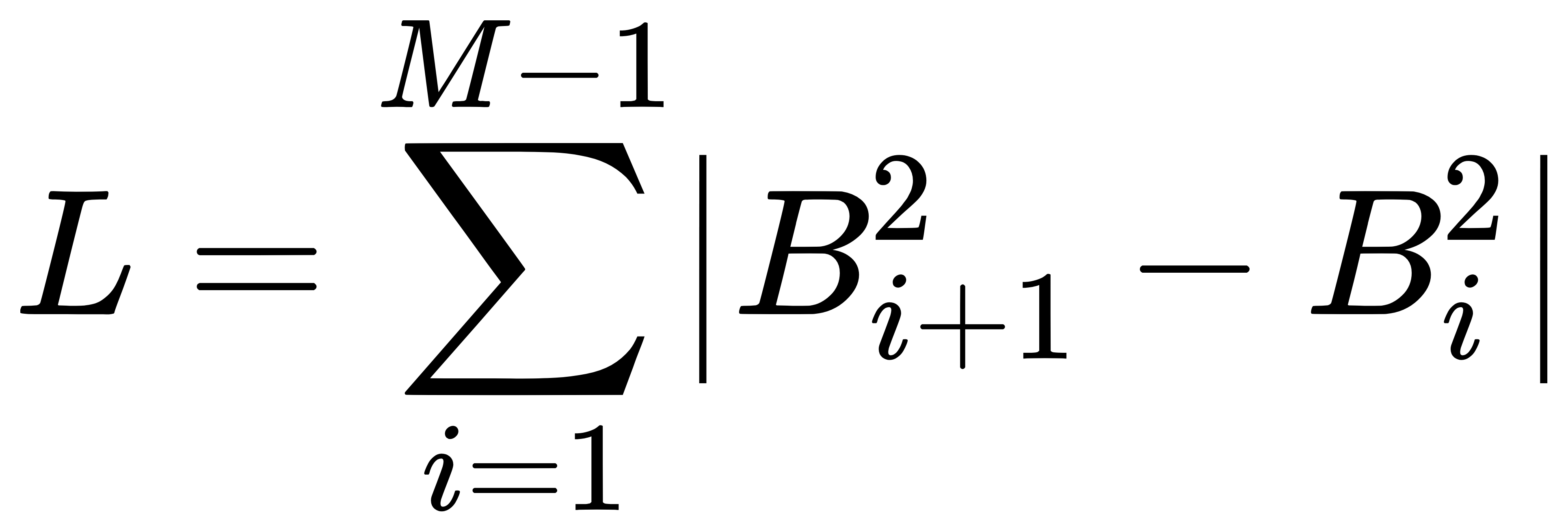
















 634
634

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








