航空三字代码表_大数据时代航空公司该如何转型（二）

数据探索分析

从航空公司系统内的客户基本信息、乘机信息以及积分信息等详细数据中，根据末次飞行日期(LAST_FLIGHT_DATE)，以2014年3月31日为结束时间，选取宽度为两年的时间段作为分析观测窗口，抽取观测窗口2012年4月1日至2014年3月31日内有乘机记录的所有客户的详细数据形成历史数据，总共62988条记录。其中包含了如会员卡号，入会时间，性别，年龄，会员卡级别，工作地城市，工作地所在省份，工作地所在国家，观测窗口结束时间，观测窗口乘机积分，飞行公里数，飞行次数，飞行时间，乘机时间间隔，平均折扣率等44个属性，如表1所示。

表1航空公司数据属性说明

	属性名称	属性说明
客户基本信息	MEMBER_NO	会员卡号
	FFP_DATE	入会时间
	FIRST_FLIGHT_DATE	第一次飞行日期
	GENDER	性别
	FFP_TIER	会员卡级别
	WORK_CITY	工作地城市
	WORK_PROVINCE	工作地所在省份
	WORK_COUNTRY	工作地所在国家
	AGE	年龄
乘机信息	FLIGHT_COUNT	观测窗口内的飞行次数
	LOAD_TIME	观测窗口的结束时间
	LAST_TO_END	最后一次乘机时间至观测窗口结束时长
	AVG_DISCOUNT	平均折扣率
	SUM_YR	观测窗口的票价收入
	SEG_KM_SUM	观测窗口的总飞行公里数
	LAST_FLIGHT_DATE	末次飞行日期
	AVG_INTERVAL	平均乘机时间间隔
	MAX_INTERVAL	最大乘机间隔
积分信息	EXCHANGE_COUNT	积分兑换次数
	EP_SUM	总精英积分
	PROMOPTIVE_SUM	促销积分
	PARTNER_SUM	合作伙伴积分
	POINTS_SUM	总累计积分
	POINT_NOTFLIGHT	非乘机的积分变动次数
	BP_SUM	总基本积分

*数据详见：demo/data/air_data.csv。

1. 描述性统计分析

通过对原始数据观察发现数据中存在票价为空值的记录，同时存在票价最小值为0、折扣率最小值为0但总飞行公里数大于0的记录。票价为空值的数据可能是客户不存在乘机记录造成。其它的数据可能是客户乘坐0折机票或者积分兑换造成。

查找每列属性观测值中空值个数、最大值、最小值，如代码清单1所示。

代码清单1数据探索

# 对数据进行基本的探索 # 返回缺失值个数以及最大最小值 import pandas as pd datafile= '../data/air_data.csv'  # 航空原始数据,第一行为属性标签 resultfile = '../tmp/explore.csv'  # 数据探索结果表 # 读取原始数据，指定UTF-8编码(需要用文本编辑器将数据装换为UTF-8编码) data = pd.read_csv(datafile, encoding = 'utf-8') # 包括对数据的基本描述，percentiles参数是指定计算多少的分位数表(如1/4分位数、中位数等) explore = data.describe(percentiles = [], include = 'all').T # describe()函数自动计算非空值数，需要手动计算空值数 explore['null'] = len(data)-explore['count'] explore = explore[['null', 'max', 'min']] explore.columns = [u'空值数', u'最大值', u'最小值']  # 表头重命名 ''' 这里只选取部分探索结果。 describe()函数自动计算的字段有count(非空值数)、unique(唯一值数)、top(频数最高者)、 freq(最高频数)、mean(平均值)、std(方差)、min(最小值)、50%(中位数)、max(最大值) ''' explore.to_csv(resultfile)  # 导出结果

*代码详见：demo/code/data_explore.py。

根据代码清单 71得到的探索结果见表2。

表2数据探索分析结果表

属性名称	空值记录数	最大值	最小值
SUM_YR_1	551	239560	0
SUM_YR_2	138	234188	0
…	…	…	…
SEG_KM_SUM	0	580717	368
avg_discount	0	1.5	0

2. 分布分析

分别从客户基本信息、乘机信息、积分信息3个角度进行数据探索，寻找客户的分布规律。

(1) 客户基本信息分布分析

选取客户基本信息中入会时间、性别、会员卡级别和年龄字段进行探索分析，探索客户的基本信息分布状况，如代码清单2所示。

代码清单 2 探索客户的基本信息分布状况

# 客户信息类别 # 提取会员入会年份 from datetime import datetime ffp = data['FFP_DATE'].apply(lambda x:datetime.strptime(x,'%Y/%m/%d')) ffp_year = ffp.map(lambda x : x.year) # 绘制各年份会员入会人数直方图 fig = plt.figure(figsize=(8 ,5))  # 设置画布大小 plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示 plt.rcParams['axes.unicode_minus'] = False plt.hist(ffp_year, bins='auto', color='#0504aa') plt.xlabel('年份') plt.ylabel('入会人数') plt.title('各年份会员入会人数') plt.show() plt.close # 提取会员不同性别人数 male = pd.value_counts(data['GENDER'])['男'] female = pd.value_counts(data['GENDER'])['女'] # 绘制会员性别比例饼图 fig = plt.figure(figsize=(7 ,4))  # 设置画布大小 plt.pie([ male, female], labels=['男','女'], colors=['lightskyblue', 'lightcoral'],        autopct='%1.1f%%') plt.title('会员性别比例') plt.show() plt.close # 提取不同级别会员的人数 lv_four = pd.value_counts(data['FFP_TIER'])[4] lv_five = pd.value_counts(data['FFP_TIER'])[5] lv_six = pd.value_counts(data['FFP_TIER'])[6] # 绘制会员各级别人数条形图 fig = plt.figure(figsize=(8 ,5))  # 设置画布大小 plt.bar(left=range(3), height=[lv_four,lv_five,lv_six], width=0.4, alpha=0.8, color='skyblue') plt.xticks([index for index in range(3)], ['4','5','6']) plt.xlabel('会员等级') plt.ylabel('会员人数') plt.title('会员各级别人数') plt.show() plt.close() # 提取会员年龄 age = data['AGE'].dropna() age = age.astype('int64') # 绘制会员年龄分布箱型图 fig = plt.figure(figsize=(5 ,10)) plt.boxplot(age,             patch_artist=True,             labels = ['会员年龄'],  # 设置x轴标题             boxprops = {'facecolor':'lightblue'})  # 设置填充颜色 plt.title('会员年龄分布箱线图') # 显示y坐标轴的底线 plt.grid(axis='y') plt.show() plt.close

*代码详见：demo/code/data_distribution.py。

通过代码清单2得到各年份会员入会人数直方图，如图2所示，入会人数随年份增长而增加在2012年达到最高峰。

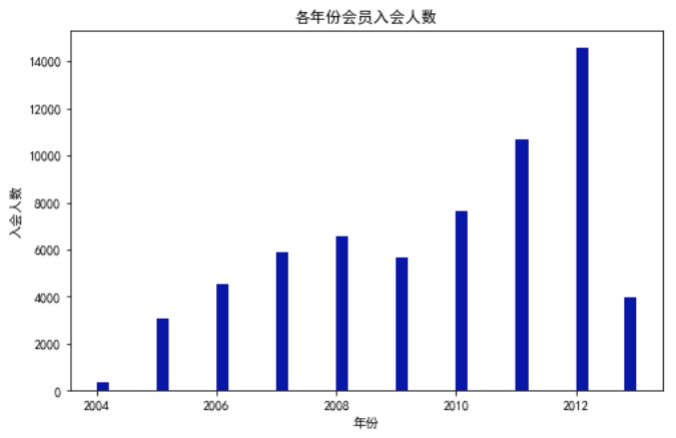
图2 各年份会员入会人数

通过代码清单2得到会员性别比例饼图，如图3所示，可以看出男性会员明显比女性会员多。

图 3 会员性别比例

通过代码清单2得到会员各级别人数条形图，如图4所示，可以看出绝大部分会员为4级会员，仅有少数会员为5级和6级会员。

图4 会员各级别人数

得到会员年龄分布箱型图，如图 5所示，可以看出大部分会员年龄集中在30~50岁之间，极少量的会员年龄小于20岁或高于60岁，且存在一个超过100岁的异常数据。

图 5会员年龄分布

(2) 客户乘机信息分布分析

选取最后一次乘机至结束的时长、客户乘机信息中飞行次数、总飞行公里数进行探索分析，探索客户的乘机信息分布状况，如代码清单3所示。

代码清单3探索客户乘机信息分布状况

lte = data['LAST_TO_END'] fc = data['FLIGHT_COUNT'] sks = data['SEG_KM_SUM'] # 绘制最后乘机至结束时长箱线图 fig = plt.figure(figsize=(5 ,8)) plt.boxplot(lte,             patch_artist=True,             labels = ['时长'],  # 设置x轴标题             boxprops = {'facecolor':'lightblue'})  # 设置填充颜色 plt.title('会员最后乘机至结束时长分布箱线图') # 显示y坐标轴的底线 plt.grid(axis='y') plt.show() plt.close # 绘制客户飞行次数箱线图 fig = plt.figure(figsize=(5 ,8)) plt.boxplot(fc,             patch_artist=True,             labels = ['飞行次数'],  # 设置x轴标题             boxprops = {'facecolor':'lightblue'})  # 设置填充颜色 plt.title('会员飞行次数分布箱线图') # 显示y坐标轴的底线 plt.grid(axis='y') plt.show() plt.close # 绘制客户总飞行公里数箱线图 fig = plt.figure(figsize=(5 ,10)) plt.boxplot(sks,             patch_artist=True,             labels = ['总飞行公里数'],  # 设置x轴标题             boxprops = {'facecolor':'lightblue'})  # 设置填充颜色 plt.title('客户总飞行公里数箱线图') # 显示y坐标轴的底线 plt.grid(axis='y') plt.show() plt.close

*代码详见：demo/code/data_distribution.py。

通过代码清单3得到客户最后一次乘机至结束的时长、客户乘机信息中飞行次数、总飞行公里数的箱线图如图 6、图7所示。

图 6客户最后一次乘机至结束的时长箱线图

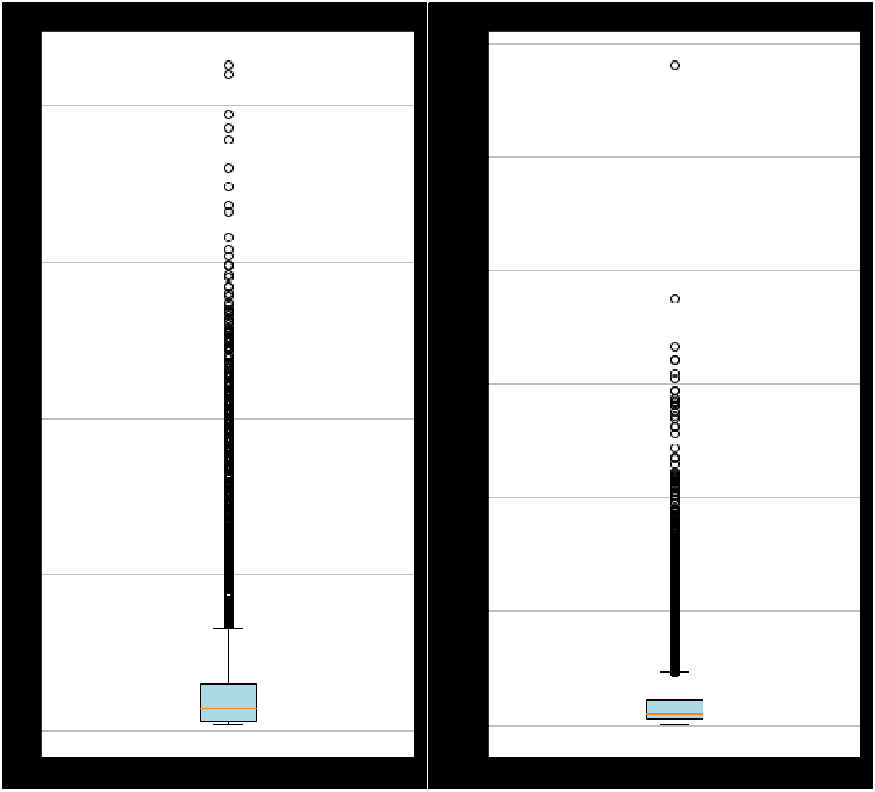
图 7客户飞行次数与总飞行公里数的箱线图

如图 6所示，客户的入会时长主要分布在50~300的区间内，另外有一部分客户群体分布在600以上的区间，可分为两个群体。如图 7所示，客户的飞行次数与总飞行公里数也明显的分为两个群体，大部分客户集中在箱线图的中的下方的箱体中，少数客户分散分布在箱体上界的上方，这部分用户很可能是高价值客户，因为其飞行次数和总飞行公里数明显超过在箱体内的客户。

(3) 客户积分信息分布分析

选取积分兑换次数、总累计积分进行探索分析，探索客户的积分信息分布状况，如代码清单4所示。

代码清单4探索客户积分信息分布状况

# 积分信息类别 # 提取会员积分兑换次数 ec = data['EXCHANGE_COUNT'] # 绘制会员兑换积分次数直方图 fig = plt.figure(figsize=(8 ,5))  # 设置画布大小 plt.hist(ec, bins=5, color='#0504aa') plt.xlabel('兑换次数') plt.ylabel('会员人数') plt.title('会员兑换积分次数分布直方图') plt.show() plt.close # 提取会员总累计积分 ps = data['Points_Sum'] # 绘制会员总累计积分箱线图 fig = plt.figure(figsize=(5 ,8)) plt.boxplot(ps,             patch_artist=True,             labels = ['总累计积分'],  # 设置x轴标题             boxprops = {'facecolor':'lightblue'})  # 设置填充颜色 plt.title('客户总累计积分箱线图') # 显示y坐标轴的底线 plt.grid(axis='y') plt.show() plt.close

*代码详见：demo/code/data_distribution.py。

通过代码清单4得到客户积分兑换次数直方图和总累计积分分布箱线图，分别如图 8、图9所示。

图8客户积分兑换次数直方图

图 9客户总累计积分

通过图 8可以看出，绝大部分客户的兑换次数在0~10的区间内，这表示大部分客户都很少进行积分兑换。通过图 9可以看出，一部分客户集中在箱体中，少部分客户分散分布在箱体上方，这部分客户的积分要明显高于箱体内的客户。

3. 相关性分析

客户信息的属性间存在相关性，选取入会时间、会员卡级别、客户年龄、飞行次数、总飞行公里数、最近一次乘机至结束时长、积分兑换次数、总累计积分属性，通过相关系数矩阵与热力图分析各属性间的相关性，如代码清单5所示。

代码清单 5相关系数矩阵与热力图

# 提取属性并合并为新数据集 data_corr = data[['FFP_TIER','FLIGHT_COUNT','LAST_TO_END',                   'SEG_KM_SUM','EXCHANGE_COUNT','Points_Sum']] age1 = data['AGE'].fillna(0) data_corr['AGE'] = age1.astype('int64') data_corr['ffp_year'] = ffp_year # 计算相关性矩阵 dt_corr = data_corr.corr(method='pearson') print('相关性矩阵为：\n',dt_corr) # 绘制热力图 import seaborn as sns plt.subplots(figsize=(10, 10)) # 设置画面大小 sns.heatmap(dt_corr, annot=True, vmax=1, square=True, cmap='Blues') plt.show() plt.close

*代码详见：demo/code/data_distribution.py。

通过代码清单5得到相关系数矩阵如表3所示，得到热力图如图10所示，可以看出部分属性间具有较强的相关性，如FLIGHT_COUNT(飞行次数)属性与SEG_KM_SUM(总公里数)属性；也有部分属性与其他属性的相关性都较弱，如AGE(年龄)属性与EXCHANGE_COUNT(积分兑换次数)属性。

表 3 相关系数矩阵

相关系数	FFP_TIER	FLIGHT_COUNT	LAST_TO_END	SEG_KM_SUM	EXCHANGE_COUNT	Points_Sum	AGE	ffp_year
FFP_TIER	1.000000	0.582447	-0.206313	0.522350	0.342355	0.559249	0.076245	-0.116510
FLIGHT_COUNT	0.582447	1.000000	-0.404999	0.850411	0.502501	0.747092	0.075309	-0.188181
LAST_TO_END	-0.206313	-0.404999	1.000000	-0.369509	-0.169717	-0.292027	-0.027654	0.117913
SEG_KM_SUM	0.522350	0.850411	-0.369509	1.000000	0.507819	0.853014	0.087285	-0.171508
EXCHANGE_COUNT	0.342355	0.502501	-0.169717	0.507819	1.000000	0.578581	0.032760	-0.216610
Points_Sum	0.559249	0.747092	-0.292027	0.853014	0.578581	1.000000	0.074887	-0.163431
AGE	0.076245	0.075309	-0.027654	0.087285	0.032760	0.074887	1.000000	-0.242579
ffp_year	-0.116510	-0.188181	0.117913	-0.171508	-0.216610	-0.163431	-0.242579	1.000000

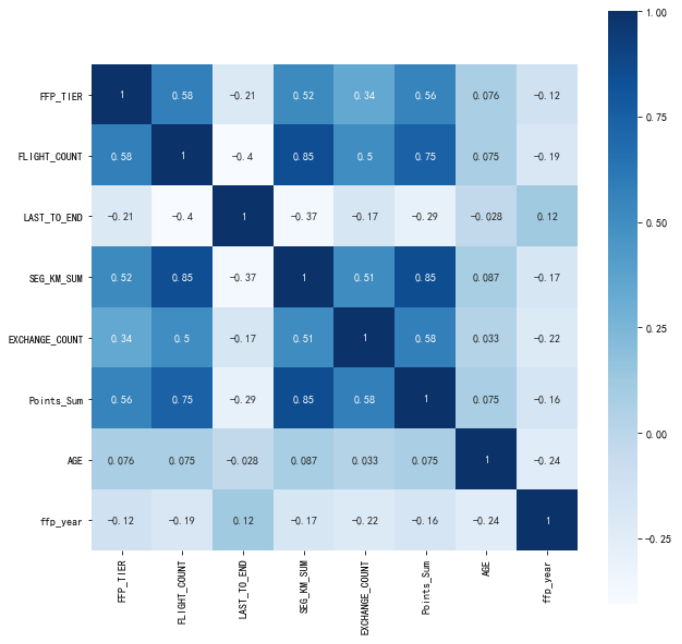
图 10热力图

Python数据挖掘分析特训营

课程简介：

了解数据挖掘的概念和范畴，掌握探索性数据分析(EDA)的常用方法，熟练使用若干种聚类算法/预测算法/异常检测算法，熟练使用数据挖掘竞赛中最常用的两种模型(随机森林/GBDT)，学会实战中提升模型性能最常用的方法(超参数优化/集成学习)

最终产出：

针对FIFA数据集，撰写完整的全流程数据分析报告

上课时间：

vol.3 开课时间：10月15日-10月30日

适合人群：

• 对数据处理、数据挖掘、Python感兴趣的人群
• 将来从事咨询、会计、快消、金融、互联网、房地产等等需要数据分析技能的行业，提升职场竞争力

• 适用于数据科学/数据分析/统计/计算机/商业分析/金融工程/工业工程和运筹学/信息系统等方向的留学申请者

• 入学标准：需要Python(掌握numpy/pandas/函数创建/数据类型与运算符/条件和循环语句)、数学或统计基础

这样良心的特训营

不囤我都替你感到亏

↓ 到手仅需 499 元 ↓

添加班主任点点即可咨询

微信：DigQuantVIP

DigQuant

   点宽学院   

从高校到企业、从理论到实践的最后一公里

⬇️⬇️⬇️