将三角形绕点b顺时针旋转90度_九年级数学旋转复习

一、复习目标

1.理解并掌握旋转的性质．

2. 能够按要求作出简单平面图形旋转后的图形，欣赏旋转在现实生活中的应用．

3. 理解中心对称的有关概念及其基本性质，了解中心对称与旋转的关系． 理解中心对称图形的概念及其基本性质，了解平行四边形、圆是中心对称图形．

4. 会判断一个图形是否是中心对称图形，能找出中心对称图形的对称中心．

5. 理解两个点关于原点对称时，它们的坐标符号相反，即点P(x，y)关于原点的对称点为P′(－x，－y)．能画出已知图形关于原点对称的图形.

重点：旋转的性质、中心对称性质的应用

难点：旋转性质的应用.

二、新课导入

专题一、旋转的性质

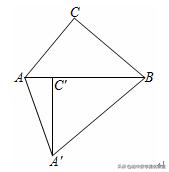
例1(2020•大连)如图，△ABC中，∠ACB＝90°，∠ABC＝40°．将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是(　　)

A．50° 　　　　　　　B．70°　　 C．110° 　　　　　　　　　　D．120°

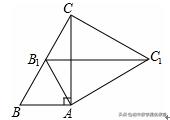
例2　(2020•眉山)如图，在Rt△ABC中，∠BAC＝90°，AB＝2．将△ABC绕点A按顺时针方向旋转至△AB1C1的位置，点B1恰好落在边BC的中点处，则CC1的长为　　　　．

专题二、中心对称图形

例3．下面四个标志是中心对称图形的是( )

　例4　如图，下列图形既是中心对称图形又是轴对称图形的是(　　)

专题三　关于原点对称

例5　已知点A(x，y－4)与点B(1－y，2x)关于原点对称，求xy的值；

专题四、旋转与点的坐标

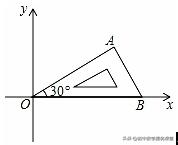
例6　将含有30°角的直角三角板如图放置在平面直角坐标系中，OB在x轴上，将三角板绕原点O顺时针旋转75°，若OA＝4，则点A的对应点A′的坐标为____________．

专题五、添辅助线解决与旋转有关的问题

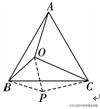
例7．等边三角形内有一点O，已知OA＝4，OB＝3，OC＝5，求∠AOB的度数．

二、回顾与反思

通过以上内容，你还觉得自己在哪些方面存在疑惑，你掌握了哪些内容？

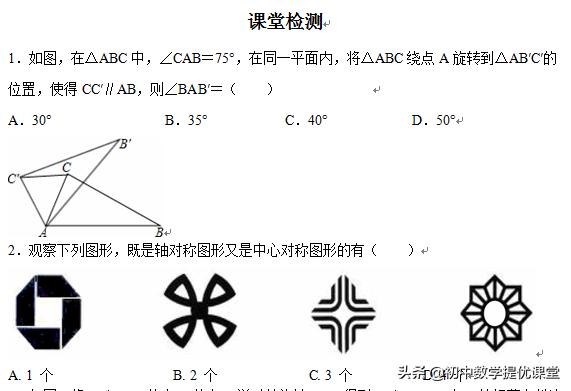
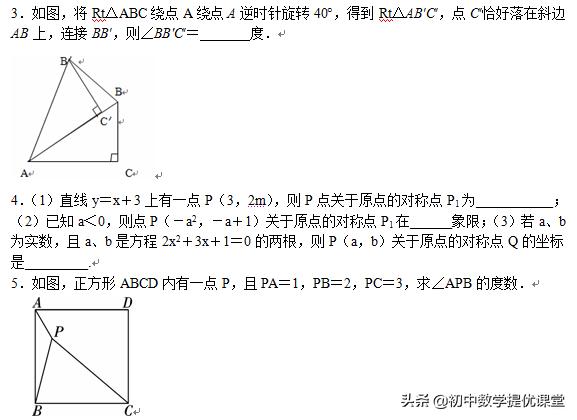
三、课堂检测(每小题20分共100分，时间5－8分钟)

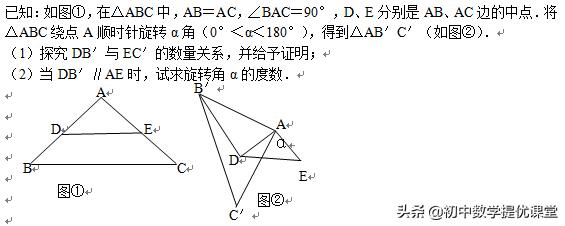
四、每日一题(提高题)