机器学习基础(泛化：机器学习的目标)

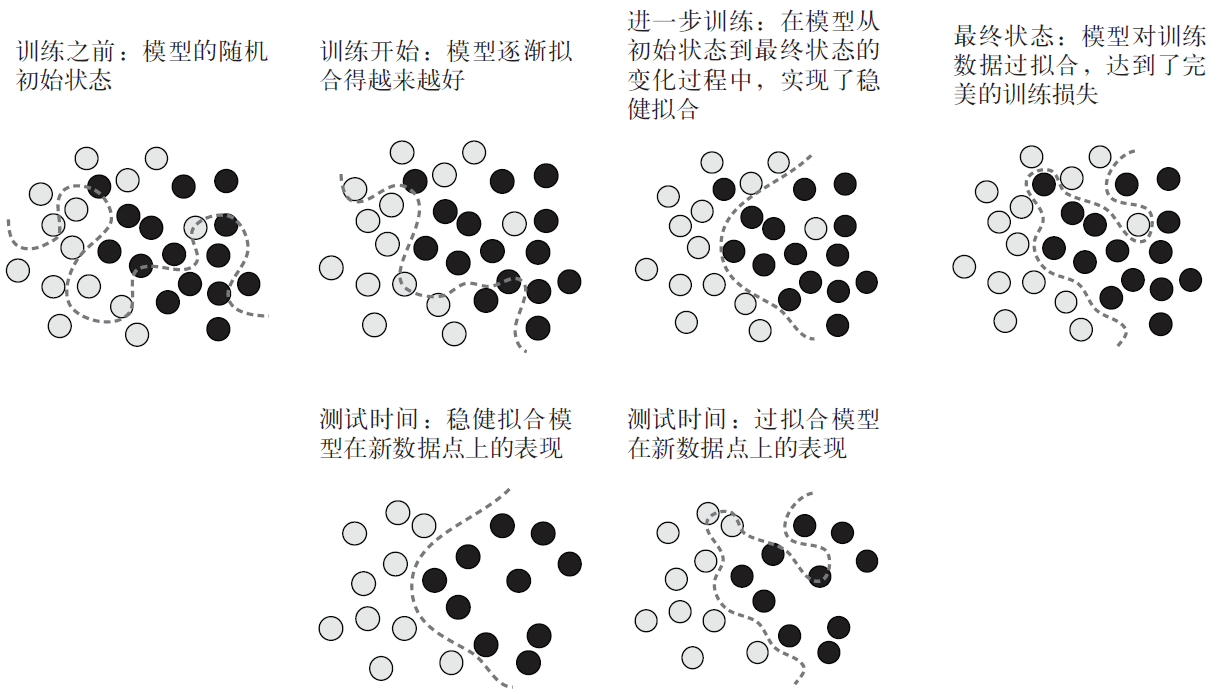
泛化：机器学习的目标

在第4 章介绍的3 个例子中（影评分类、新闻分类和房价预测），我们将数据划分为训练集、
验证集和测试集。不在同样的训练数据上评估模型的原因显而易见：仅仅几轮过后，模型在前
所未见的数据上的性能就开始与训练数据上的性能发生偏离，后者总是随着训练而提高。模型
开始过拟合。所有机器学习问题都存在过拟合。

机器学习的根本问题在于优化与泛化之间的矛盾。优化（optimization）是指调节模型使其
在训练数据上得到最佳性能的过程（对应机器学习中的学习），泛化（generalization）则是指训
练好的模型在前所未见的数据上的性能。机器学习的目标当然是得到良好的泛化，但你无法控
制泛化，只能让模型对训练数据进行拟合。如果拟合得太好，就会出现过拟合，从而影响泛化。
但究竟是什么导致了过拟合？我们如何才能实现良好的泛化？

欠拟合与过拟合

对于第4 章的模型，随着训练的进行，模型在留出的验证数据上的性能开始提高，然后不
可避免地在一段时间后达到峰值。图5-1 所示的模式非常普遍，你会在所有模型和所有数据集
中遇到。

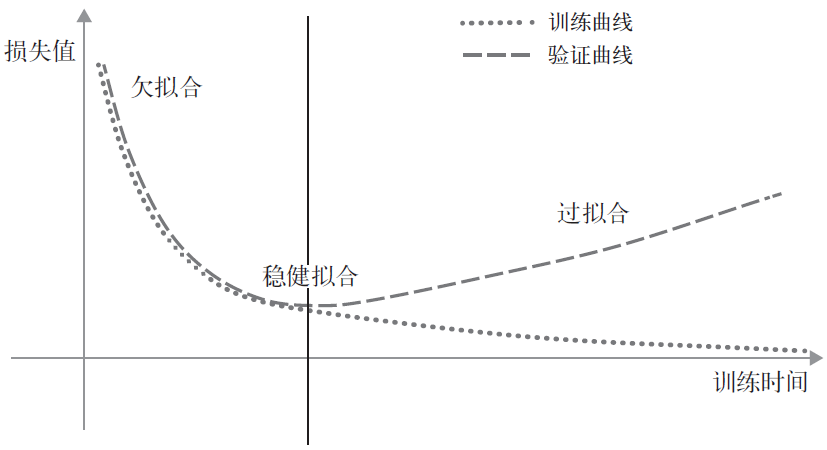
训练开始时，优化和泛化是相关的：训练数据上的损失越小，测试数据上的损失也越小。
这时，模型是欠拟合（underfit）的，即仍有改进的空间，模型还没有对训练数据中的所有相关
模式建模。但在训练数据上迭代一定次数之后，泛化能力就不再提高，验证指标先是不变，然
后开始变差。这时模型开始过拟合，它开始学习仅和训练数据有关的模式，但对新数据而言，
这些模式是错误的或是不相关的。

如果数据的不确定性很大或者包含罕见的特征，那么就特别容易出现过拟合。我们来看几
个具体的例子。

1. 嘈杂的训练数据

在现实世界的数据集中，有些输入是无法识别的，这很常见。例如，MNIST 数字图像可能
是一张全黑的图像，或者像图5-2 那样。

这些是什么数字？我也不知道。但它们都是MNIST 训练集的一部分。更糟糕的一种情况是，
输入是有效的，但标签是错误的，如图5-3 所示。

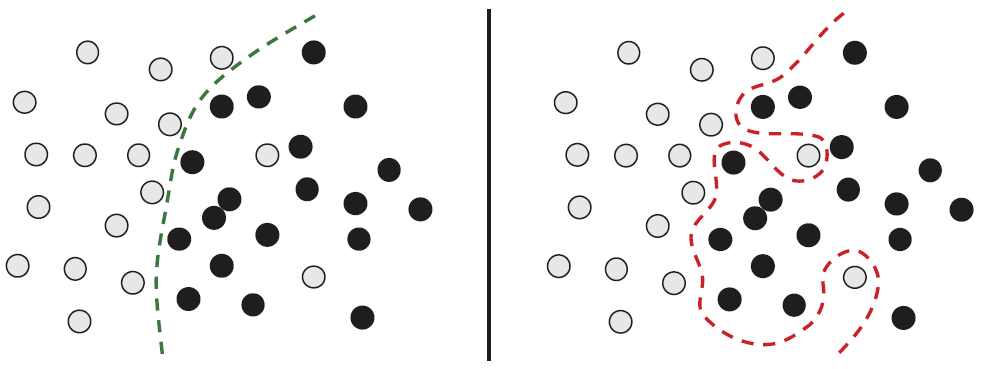
如果模型将这些异常值全部考虑进去，那么它的泛化性能将会下降，如图5-4 所示。如果
一个手写的4 与图5-3 中标签错误的4 看起来非常相似，那么它很可能会被归类为数字9。

2. 模糊特征

并不是所有数据噪声都来自于误差——如果问题包含不确定性和模糊性，那么即使是完全
干净且标记整齐的数据也会存在噪声。对于分类任务，经常出现输入特征空间的某些区域与多
个类别同时相关的情况。假设你正在开发一个模型，它接收香蕉图像作为输入，并预测香蕉是
未成熟的、成熟的还是腐烂的。这些类别之间没有明确的界限，同一张图片可能会被不同的人
标记为未成熟或成熟。同样，许多问题包含随机性。你可以利用气压数据来预测明天是否下雨，
但即使测量数据完全相同，第二天也可能有时下雨，有时晴天，二者皆有一定的概率。

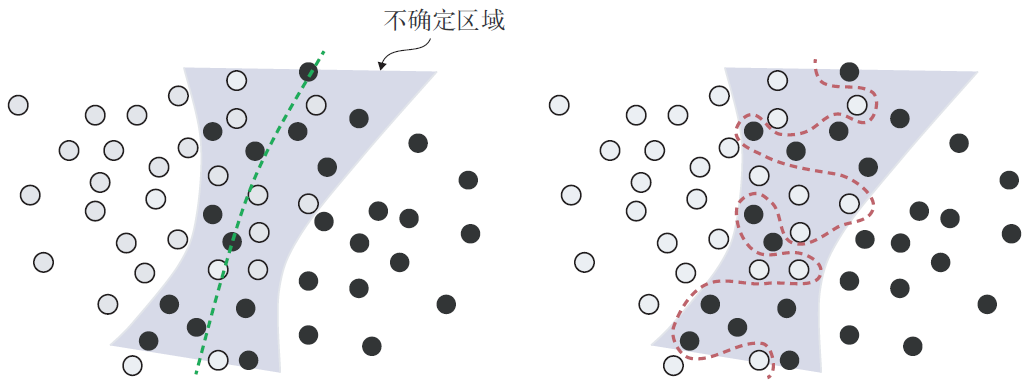
模型可能会对特征空间的不确定区域过于自信，从而对这种概率数据过拟合，如图5-5 所示。
更稳健的拟合将忽略个别数据点，而着眼于大局。

3. 罕见特征与虚假的相关性

如果你一生中只见过两只橙色的虎斑猫，而且它们碰巧都非常不合群，那么你可能会得出
这样的结论：橙色的虎斑猫通常不合群。这就是过拟合。如果你接触过更多品种的猫，包括更
多橙色的猫，你就会知道，猫的颜色与性格并没有太大的相关性。

同样，如果机器学习模型在包含罕见特征的数据集上进行训练，也很容易出现过拟合。对
于一项情感分类任务，如果“番荔枝”（cherimoya，一种原产于安第斯山脉的水果）这个词只
出现在训练数据的一个文本中，而这个文本的情感恰好是负面的，那么一个没有做好正则化
的模型可能会对这个词赋予很高的权重，并且总把提到番荔枝的新文本归类为负面的。然而客
观地说，番荔枝这个词并没有包含负面情绪。

重要的是，一个特征值出现次数较多，也会导致虚假的相关性。假设一个单词出现在训练
数据的100 个样本中，其中54% 与正面情绪相关，46% 与负面情绪相关。这种差异很可能完全
是统计上的偶然情况，但你的模型很可能学会利用这个特征来完成分类任务。这是过拟合最常
见的来源之一。

下面来看一个惊人的例子。对于MNIST 数据集，将784 个白噪声维度连接到现有的784
个数据维度中，从而创建一个新的训练集：现在一半的数据都是噪声。为了对比，还可以连接
784 个全零维度来创建一个等效的数据集，如代码清单5-1 所示。连接无意义的特征根本不影响
数据所包含的信息，我们只是添加了一些内容。人类的分类精度根本不会受到这些变换的影响。

代码清单5-1 向MNIST 数据集添加白噪声通道或全零通道

from tensorflow.keras.datasets import mnist
import numpy as np
(train_images, train_labels), _ = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
train_images_with_noise_channels = np.concatenate(
[train_images, np.random.random((len(train_images), 784))], axis=1)
train_images_with_zeros_channels = np.concatenate(
[train_images, np.zeros((len(train_images), 784))], axis=1)

下面我们在这两个训练集上训练第2 章的模型，如代码清单5-2 所示。

代码清单5-2 对于带有噪声通道或全零通道的MNIST 数据，训练相同的模型

from tensorflow import keras
from tensorflow.keras import layers
def get_model():
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
return model
model = get_model()
history_noise = model.fit(
train_images_with_noise_channels, train_labels,
epochs=10,
batch_size=128,
validation_split=0.2)
model = get_model()
history_zeros = model.fit(
train_images_with_zeros_channels, train_labels,
epochs=10,
batch_size=128,
validation_split=0.2)

我们来比较两个模型的验证精度如何随时间变化，如代码清单5-3 所示。

代码清单5-3 绘图比较验证精度

import matplotlib.pyplot as plt
val_acc_noise = history_noise.history["val_accuracy"]
val_acc_zeros = history_zeros.history["val_accuracy"]
epochs = range(1, 11)
plt.plot(epochs, val_acc_noise, "b-",
label="Validation accuracy with noise channels")
plt.plot(epochs, val_acc_zeros, "b--",
label="Validation accuracy with zeros channels")
plt.title("Effect of noise channels on validation accuracy")
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend()

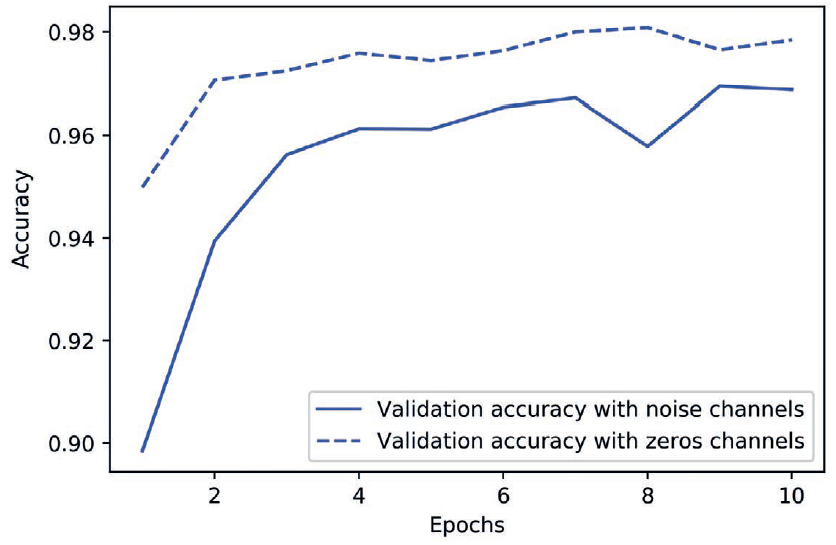
尽管二者的数据都包含相同的信息，但在带有噪声通道的数据集上训练的模型，最终验证
精度要低约1%（见图5-6），这完全是由于虚假相关性的影响。添加的噪声通道越多，精度就会
下降得越多。

噪声特征不可避免会导致过拟合。因此，如果你不确定特征究竟是有用的还是无关紧要的，
那么常见的做法是在训练前进行特征选择（feature selection）。例如，将IMDB 数据限制为前
10 000 个最常出现的单词，就是一种粗略的特征选择。特征选择的常用方法是对每个特征计算
有用性分数，并且只保留那些分数高于某个阈值的特征。有用性分数（usefulness score）是用于
衡量特征对于任务来说所包含信息量大小的指标，比如特征与标签之间的互信息。这么做可以
过滤前面例子中的白噪声通道。

深度学习泛化的本质

关于深度学习模型的一个值得注意的事实是，只要模型具有足够的表示能力，就可以训练
模型拟合任何数据。

不信吗？你可以试着把MNIST 数据集的标签打乱，然后在打乱后的数据集上训练一个模
型，如代码清单5-4 所示。尽管输入与打乱后的标签之间毫无关系，但训练损失下降得不错，
而这只是一个相对较小的模型。当然，验证损失不会随着时间的推移有任何改善，因为在这种
情况下不可能泛化。

代码清单5-4 将标签随机打乱，拟合一个MNIST 模型

(train_images, train_labels), _ = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255

random_train_labels = train_labels[:]
np.random.shuffle(random_train_labels)
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
model.fit(train_images, random_train_labels,
epochs=100,
batch_size=128,
validation_split=0.2)

事实上，你甚至不需要用MNIST 数据来做这件事，而可以直接生成白噪声输入和随机标签。
只要模型具有足够多的参数，也可以对这些数据进行拟合。模型最终只会记住特定的输入，就
像Python 字典一样。

如果是这样，那么深度学习模型为什么能够泛化？它不应该只是学会了训练输入与目标之
间的一种特别的映射，就像花哨的字典一样吗？我们怎么能指望这种映射会对新输入起作用呢？

事实证明，深度学习泛化的本质与深度学习模型本身关系不大，而与现实世界中的信息结
构密切相关。我们来具体解释一下。

1. 流形假说

MNIST 分类器的输入（在预处理之前）是一个由0 ～ 255 的整数组成的28×28 数组。因此，
输入值的总数为256 的784 次幂，这远远大于宇宙中的原子数目。但是，这些输入中只有少数
看起来像是有效的MNIST 样本，也就是说，在所有可能的28×28 uint8 数组组成的父空间中，
真实的手写数字只占据一个很小的子空间。更重要的是，这个子空间不仅仅是父空间中随机散
布的一组点，而是高度结构化的。

首先，有效手写数字的子空间是连续的：如果取一个样本并稍加修改，那么它仍然可以被
识别为同一个手写数字。其次，有效子空间中的所有样本都由穿过子空间的光滑路径连接。也
就是说，如果你取两个随机的MNIST 数字A 和B，就会存在将A 变形成B 的一系列“中间”
图像，其中每两幅相邻图像都非常相似（见图5-7）。在两个类别的边界附近可能会有一些模棱
两可的形状，但这些形状看起来仍然很像数字。

用术语来说，手写数字在28×28 uint8 数组的可能性空间中构成了一个流形（manifold）。
这个词看起来很高深，但其概念非常直观。“流形”是指某个父空间的低维子空间，它局部近似
于一个线性空间（欧几里得空间）。例如，平面上的光滑曲线就是二维空间中的一维流形，因为
对于曲线上的每一点，你都可以画出一条切线（曲线上的每一点都可以用直线来近似）。三维空
间中的光滑表面是一个二维流形，以此类推。

更一般地说，流形假说（manifold hypothesis）假定，所有自然数据都位于高维空间中的一
个低维流形中，这个高维空间是数据编码空间。这是关于宇宙信息结构的一个非常有力的表述。
据我们目前所知，这个表述是准确的，这也是深度学习有效的原因。它不仅适用于MNIST 手写
数字，也适用于树木形态、人脸、人声甚至自然语言。

流形假说意味着：

• 机器学习模型只需在其输入空间中拟合相对简单、低维、高度结构化的子空间（潜在流
  形）；
• 在其中一个流形中，总是可以在两个输入之间进行插值（interpolate），也就是说，通过
  一条连续路径将一个输入变形为另一个输入，这条路径上的所有点都位于流形中。

能够在样本之间进行插值是理解深度学习泛化的关键。

如果你处理的是可插值的数据点，那么你可以开始理解前所未见的点，方法是将其与流形
中相近的其他点联系起来。换句话说，你可以仅用空间的一个样本来理解空间的整体。你可以
用插值来填补空白。

请注意，潜在流形中的插值与父空间中的线性插值不同，如图5-8 所示。例如，两个
MNIST 手写数字的像素平均值通常不是一个有效数字。

至关重要的是，虽然深度学习实现泛化的方法是对数据流形的学习近似进行插值，但如果
认为插值就是泛化的全部，那你就错了。它只是冰山一角。插值只能帮你理解那些与之前所见
非常接近的事物，即插值可以实现局部泛化（local generalization）。但值得注意的是，人类一直
在处理极端新奇的事物，而且做得很好。你无须事先对所遇到的每一种情况训练无数次。你的
每一天与之前经历的任何一天都不同，也与人类诞生以来任何人所经历的任何一天都不同。你
可以在纽约、上海、班加罗尔分别住上一周，而无须为每个城市进行上千次的学习和排练。

人类能够进行极端泛化（extreme generalization），这是由不同于插值的认知机制实现的，包
括抽象、世界的符号模型、推理、逻辑、常识，以及关于世界的固有先验知识——我们通常称
其为理性（reason），与直觉和模式识别相对。后者的本质在很大程度上是可插值的，但前者不
是。二者对于智能都是必不可少的。我们将在第14 章中进一步讨论这个问题。

3. 深度学习为何有效

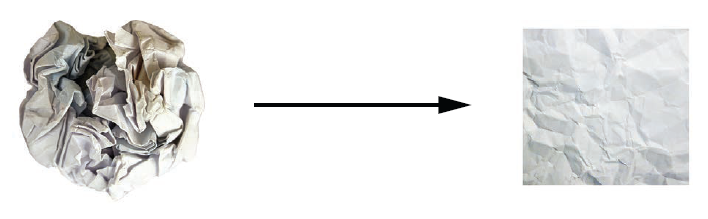
还记得第2 章中的皱纸团比喻吗？一张纸表示三维空间中的二维流形，如图5-9 所示。深
度学习模型是一个工具，用于让“纸团”恢复平整，也就是解开潜在流形。

深度学习模型本质上是一条高维曲线——一条光滑连续的曲线（模型架构预设对其结构有
额外的约束），因为它需要是可微的。通过梯度下降，这条曲线平滑、渐进地对数据点进行拟合。
就其本质而言，深度学习就是取一条大而复杂的曲线（流形）并逐步调节其参数，直到曲线拟
合了一些训练数据点。

这条曲线包含足够多的参数，可以拟合任何数据。事实上，如果对模型训练足够长的时间，
那么它最终会仅仅记住训练数据，根本没有泛化能力。然而，你要拟合的数据并不是由稀疏分
布于底层空间的孤立点组成的。你的数据在输入空间中形成一个高度结构化的低维流形，这就
是流形假说。随着梯度逐渐下降，模型曲线会平滑地拟合这些数据。因此，在训练过程中会有
一个中间点，此时模型大致接近数据的自然流形，如图5-10 所示。

在这个中间点，沿着模型学到的曲线移动近似于沿着数据的实际潜在流形移动。因此，模
型能够通过对训练输入进行插值来理解前所未见的输入。

深度学习模型不仅具有足够的表示能力，还具有以下特性，使其特别适合学习潜在流形。

• 深度学习模型实现了从输入到输出的光滑连续映射。它必须是光滑连续的，因为它必须
  是可微的（否则无法进行梯度下降）。这种光滑性有助于逼近具有相同属性的潜在流形。
• 深度学习模型的结构往往反映了训练数据中的信息“形状”（通过架构预设）。这对于图
  像处理模型（见第8 章和第9 章）和序列处理模型（见第10 章）来说尤其如此。更一
  般地说，深度神经网络以分层和模块化的方式组织学到的表示，这与自然数据的组织方
  式相呼应。

4. 训练数据至关重要

虽然深度学习确实很适合流形学习，但泛化能力更多是自然数据结构的结果，而不是模型
任何属性的结果。只有数据形成一个可以插值的流形，模型才能够泛化。特征包含的信息量
越大、特征噪声越小，泛化能力就越强，因为输入空间更简单，结构也更合理。数据管理和特
征工程对于泛化至关重要。

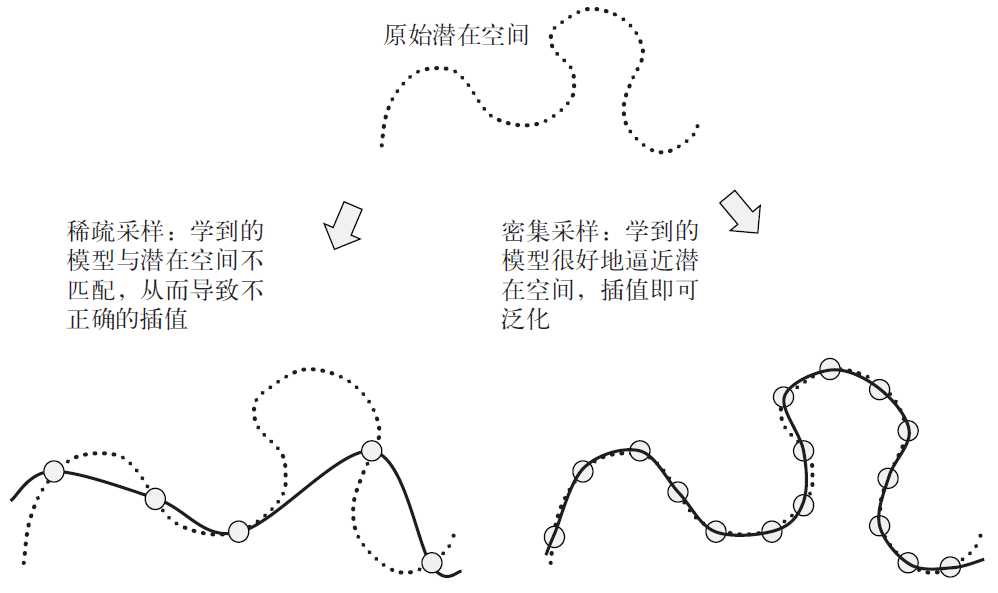
此外，由于深度学习是曲线拟合，因此为了使模型表现良好，需要在输入空间的密集采样
上训练模型。这里的“密集采样”是指训练数据应该密集地覆盖整个输入数据流形，如图5-11
所示。在决策边界附近尤其应该如此。有了足够密集的采样，就可以理解新输入，方法是在以
前的训练输入之间进行插值，无须使用常识、抽象推理或关于世界的外部知识——这些都是机
器学习模型无法获取的。

应该始终记住，改进深度学习模型的最佳方法就是在更多的数据或更好的数据上训练模型
（当然，添加过于嘈杂的数据或不准确的数据会降低泛化能力）。对输入数据流形进行更密集的
采样，可以得到泛化能力更强的模型。除了在训练样本之间进行粗略的插值，你不应指望深度
学习模型有更强的表现。因此，应该努力使插值尽可能简单。深度学习模型的性能仅由以下两
项输入决定：模型架构预设与模型训练数据。

如果无法获取更多数据，次优解决方法是调节模型允许存储的信息量，或者对模型曲线的
平滑度添加约束。如果一个神经网络只能记住几种模式或非常有规律的模式，那么优化过程将
迫使模型专注于最显著的模式，从而更可能得到良好的泛化。这种降低过拟合的方法叫作正则
化（regularization）。5.4.4 节将深入介绍正则化方法。
在开始调节模型以提高泛化能力之前，你需要一种能够评估模型当前性能的方法。在5.2
节中，我们将学习如何在模型开发过程中监控泛化能力，即模型评估。