深入理解计算机系统(CSAPP):第二章.信息的表示和处理

JJge97

已于 2023-09-01 09:46:45 修改

阅读量111

点赞数

分类专栏：深入理解计算机系统 csapp 文章标签：计算机网络

于 2023-08-23 15:54:44 首次发布

本文链接：https://blog.csdn.net/weixin_42314827/article/details/132444803

版权

深入理解计算机系统同时被 2 个专栏收录

5 篇文章 0 订阅

订阅专栏

csapp

5 篇文章 0 订阅

订阅专栏

2.3 整数运算

许多刚入门的程序员非常惊奇的发现，两个正数相加会得出一个负数，而比较表达式 x<y 和 x-y<0会产生不同的结果。这些属性是由计算机运算的有限性造成的。

2.3.1 无符号加法

考虑两个非负整数x和y 满足 $0 \leq x , y< 2^{w}$ 。每个数都能表示为ω位无符号数字。然而，如果计算他们的和，我们就有一个可能的范围 $0 \leq x+y \leq 2^{w+1} -2$ 。表示这个和可能需要 ω+1 位。

例如，当x和y有4位表示时，函数x 与y 的取值范围为 0~15，但是和的取值范围是0~30。在表示定长的数据类型中，明显0~30 超过了规定的4位。如果想要保持和为一个 ω+1位的数字，并且把它加上另外一个数值，我们可能就需要ω+2个位，以此类推。这种持续的“字节膨胀”意味着，要想完整的表示算术运算的结果，我们不能对字长做任何限制。在常见的编程语言中，是支持固定的精度运算，因此像“加法”和“乘法”这样运算不同于他们在整数上的相应运算。当然也有支持无限精度运算的，例如Lisp。

让我们为参数x和y定义运算 $+_{w}^{u}$ ，其中 $0 \leq x , y< 2^{w}$ ，该操作是把整数x+y截断为ω位得到的结果，再把这个结果看做是一个无符号数。这可以被视为一种形式的模运算，对x+y的位级表示，简单丢弃任何权重大于 $2^{w+1}$ 的位就可以计算出和模 $2^{w}$ 。

比如，考虑一个4位的数字表示，x=9，y=12的位表示分别为[1001] 和[1100] 。他们的和是21，5位的表示为[10101]。如果丢弃最高位[0101]，也就是说，十进制值的5 。这就和值 $21 mod 16 = 5$ 一致。

这样，我们可以将操作 $+_{w}^{u}$ 描述为：

原理：无符号数加法。

$x+_{w}^{u}\textrm{y} = x + y ,x+y<2^{w}$ 正常

$x+_{w}^{u}\textrm{y} = x + y -2^{w},2^{w}\leq x+y\leq 2^{w-1}$ 溢出

推导：无符号数加法。

一般而言，我们可以看到如果 $x+y<2^{w}$ ，和的 ω+1位表示的最高位会等于0，因此丢弃它不会改变这个数值。另一方面，如果 $2^{w}\leq x+y\leq 2^{w-1}$ ，和的ω+1位表示的最高位会等于1，因此丢弃它就相当于从和中减去了 $2^{w}$

说一个算术运算溢出，是指完整的整数结果不能放到数据类型的字长限制中去。当两个运算数的和为 $2^{w}$ 或者更大时，就发生了溢出。

当执行c程序时，不会将溢出作为错误而发出信号。不过有的时候，我们可能希望判断是否发生了溢出。

原理：检测无符号数加法中的溢出。

对在范围 $0\leq x,y\leq UMax_{w}$ 中的x和y ，令 $s\doteq x+_{w}^{u}\textrm{y}$ ，则对计算s，当且仅当 $s< x$ (或者等价地 $s< y$ 时)，发生了溢出。

推导：检测无符号数加法中的溢出。

通过观察发现 $x+y\geq x$ ，因此如果s没有溢出，我们能够肯定 $s \geq x$ 。另一方面，如果s确实溢出了，我们就有 $s = x+y-2^{w}$ 。假设 $y<2^{w}$ ，我们就有了 $y-2^{w}<0$ ，因此 $s=x+\left ( y-2^{w} \right ) < x$

写出如果参数x和y相加不会产生溢出，就返回-1。

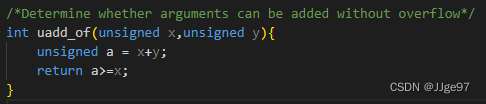
原理：无符号数求反。

对满足 $0\leq x< 2^{w}$ 的任意x，其ω位的无符号逆元 $-_{w}^{u}\textrm{x}$ 由下式给出：

$-_{w}^{u}\textrm{x} = x ,x=0$

$-_{w}^{u}\textrm{x} = 2^{w}-x ,x>0$

推导：无符号数求反。

当x=0时，加法逆元显然是0。对于x>0，考虑值 $2^{w}-x$ 。我们观察到这个数字在 $0< 2^{w}-x<2^{w}$ 范围之内，并且 $\left ( x+2^{w}-x \right ) mod 2^{w} = 2^{w}mod2^{w}=0$ ，因此，他就是x在 $+_{w}^{u}\textrm{x}$ 下的逆元。

x		$-_{4}^{u}\textrm{x}$
十六进制	十进制	十进制	十六进制
0	0	0	0
5	5	11	B
8	8	8	8
D	13	3	3
F	15	1	1

2.3.2 补码加法

对于补码加法，我们必须确定结果太大，或者结果太小时，应该做些什么。

给定在范围 $-2^{w-1} \leq x ,y\leq 2^{w-1}-1$ 之内的整数值x和y，他们和的范围在 $-2^{w} \leq x ,y\leq 2^{w}-2$ 之内，要想准确的表示，可能需要ω+1位。就像以前一样，我们将表示截断到ω位，来避免数据大小的不断扩张。然而，结果却不像模数加法那样在数学上感觉很熟悉。定义 $x+_{w}^{t}\textrm{y}$ 为整数和x+y被截断为ω位的结果，并将这个结果看做是补码数。

原理：补码加法。

对满足 $-2^{w} \leq x ,y\leq 2^{w}-2$ 的整数x和y，有

$x+_{w}^{t}\textrm{y} = x+y-2^{w},2^{w} \leq x +y$ 正溢出

$x+_{w}^{t}\textrm{y} = x+y,-2^{w} \leq x +y<2^{w-1}$ 正常

$x+_{w}^{t}\textrm{y} = x+y+2^{w}, x +y < -2^{w}$ 负溢出

原理：检测补码加法中的溢出。

对满足 $TMin_{w} \leq x,y\leq TMax_{w}$ 的x和y，令 $x\doteq x+_{w}^{t}\textrm{y}$ ，当且仅当 x>0，y>0，但s<=0时，计算s发生了正溢出。当且仅当x<0，y<0，但s>=0时，计算s发生了负溢出。

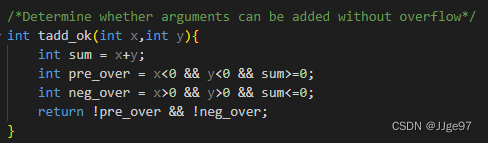
根据上述代码，请写出计算x-y不产生溢出，函数返回1。

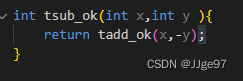
上述代码中当y=TMin时，由于计算机补码，转换成二进制操作：

 -y = ~N+1 =~1000 0000 0000 0000 0000 0000 0000 0000 +1  
           = 0111 1111 1111 1111 1111 1111 1111 1111 +1 
           = 1000 0000 0000 0000 0000 0000 0000 0000 
  = y

正常情况下，当y为 $TMin_{w}$ 时，x<0是返回1，x>0=返回0，而-y = $TMin_{w}$ ，程序认为当x为负数时溢出、x为非负数时，不溢出。

2.3.3 补码的非

可以看到范围在 $TMin_{w} \leq x \leq TMax_{w}$ 中的每个数字x 都有 $+_{w}^{t}\textrm{}$ 下的加法逆元，我们将 $-_{w}^{t}\textrm{x}$ 表示如下。

原理：补码的非。

对满足 $TMin_{w} \leq x \leq TMax_{w}$ 的x，其补码的非 $-_{w}^{t}\textrm{x}$ 由下式给出

$-_{w}^{t}\textrm{x} = TMin_{w} , x=TMin_{w}$

$-_{w}^{t}\textrm{x} = -x , x>TMin_{w}$

也就是说，对于ω位的补码加法来说， $TMin_{w}$ 是自己的加法逆，而对其他任何数字x 都有-x作为其加法的逆。

计算一个位级表示的值的补码非有几种非常聪明的方法。这些技术很有用，同时也能让你更加了解补码表示的本质。

第一种：对每一位求补，在对结果加1。在C语言中，可以说对于任意数值x，计算式表达-x 和~x+1得到的结果完全一样。

第二种是建立在将位向量分为两部分的基础之上的。假设k是最右边的1的位置，因而x的表达式为 $[x_{w-1},x_{w-2},..,x_{k-1},1,0,...,0]$ ，这个值的非就写成了 $\left [ \sim x_{w-1},\sim x_{w-2},..,\sim x_{k-1},1,0,...,0\right ]$ ，也就是说我们对位k左边的所有位取反。

2.3.4 无符号乘法

范围在 $0 \leq x , y\leq 2^{w}-1$ 内的整数x和y可以被表示为ω位的无符号数，但他们的乘积 x*y的取值范围为 $0 \sim \left ( 2^{w-1}-1 \right )^{2} = 2^{2w}-2^{w+1}+1$ 之间。这可能需要 2ω位来表示。不过，c语言中的无符号乘法被定义为产生ω位的值，就是2ω位的整数乘积的低ω为来表示的值。我们将这个值表示为 $x * _{w}^{u}\textrm{y}$

将一个无符号数截断为ω位等价于计算该值模 $2^{w}$ ，得到：

原理：无符号乘法。

对满足 $0 \leq x , y\leq UMax_{w}$ 的x和y 有：

$x*_{w}^{u}\textrm{y} = \left (x*y \right )mod 2^{w}$

2.3.5 补码乘法

范围在 $-2^{w-1} \leq x ,y\leq 2^{w-1}-1$ 内的整数x和y可以被表示为ω位的补码数字，但是他们的乘积x*y 的取值范围为 $-2^{w-1} * \left ( 2^{w-1}-1 \right ) = -2^{2w-2}+ 2^{w-1}$ 到 $-2^{w-1} * -2^{w-1} = 2^{2w-2}$ 之间，想要表达这个数字，需要2ω位来表示。然而，C语言中的有符号乘法是通过将2ω位的乘积截断为ω位来实现的。我们将这个数值表示为 $x* _{w}^{t}\textrm{y}$ 。将一个补码数截断为ω位相当于先计算该值模 $2^{w}$ ，在把无符号数转换为补码，得到

原理：补码乘法。

对满足 $TMin_{w} \leq x,y \leq TMax_{w}$ 的x和y有：

$x* _{w}^{t}\textrm{y} = U2T_{w} \left ( \left ( x*y \right ) mod2^{w} \right )$

我们认为对于无符号和补码乘法来说，乘法运算的位级表示都是一样的，并用如下原理说明

原理：无符号和补码乘法的位级等价性。

给定长度为ω的位向量 $\vec{x}$ 和 $\vec{y}$ ，用补码形式的位向量表示来定义整数x和y：

$x = B2T_{w}\left ( \vec{x} \right ),y=B2T_{w}\left ( \vec{y} \right )$

用无符号形式的维向量表示来定义非负整数 $x^{'},y^{'}$ ：

$x^{'} = B2U_{w}\left ( \vec{x} \right ),y^{'}=B2U_{w}\left ( \vec{y} \right )$

则：

$T2B_{w}\left ( x*_{w}^{t}\textrm{y} \right ) = U2B_{w} \left ( x*_{w}^{t}\textrm{y } \right )$

模式	x		y		x*y		截断的x*y
无符号	[100]	4	[101]	5	[010100]	20	[100]	4
补码	[100]	-4	[101]	-3	[001100]	12	[100]	-4
无符号	[010]	2	[111]	7	[001110]	14	[110]	6
补码	[010]	2	[111]	-1	[111110]	-2	[110]	-2
无符号	[110]	6	[110]	6	[100100]	36	[100]	4
补码	[110]	-2	[110]	-2	[000100]	4	[100]	-4

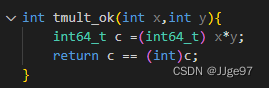
给你一个任务，开发函数tmult_ok的代码，该函数会判断两个参数相乘是否会产生溢出。下面是你的解决方案

/*Determine whether arguments can be multiplied without overflow*/
int tmult_ok(int x,int y){
    int p = x*y;
    /*Either x is zero,or dividing p by x gives y*/
    return !x || p/x == y;
}

你用了很多x和y来测试这段代码，似乎都正常工作。你的同事挑战你。

“如果我不能用减法来检验加法是否溢出，那么你怎么能用除法检验乘法是否溢出呢？”

按照下面的思路，用数学推导来证明你的方法是对的。

首先，证明x=0的情况是正确的。

另外，考虑ω位数字x、y、p和q，这里p是x和y补码乘法的结果，而q是p除以x的结果。

说明x和y的整数乘积x*y，可以写成这样的形式： $x*y = p+ t2^{w}$ ，其中 $t\neq 0$ 当且仅当p的计算溢出。
说明p可以写成这样的形式： $p=x*q+r$ ，其中 $\left | r \right | < \left | x \right |$ 。
说明q=y当且仅当 $r=t=0$ 。

练习题 2.36

练习题 2.37

/*Illustration of code vulnerability similar to that fount in 
 *Sun's XDR library  
 */
void* copy_elements(void *ele_src[],int ele_cnt,size_t ele_size){
    /**
    * Allocate buffer for ele_cnt objects,each of ele_size bytes
    * and copy from locations designated by ele_src
    */
    void *result = malloc(ele_cnt * ele_size);
    if(result == NULL)
        return NULL;
    void *next = result;
    int i;
    for(i=0;i<ele_cnt;i++){
        /*Copy object i to destination*/
        memcopy(next,ele_src[i],ele_size);
        /*move pointer*/
        next += ele_size;
    }
    return result;
}

在malloc函数中，存在乘积溢出情况，请问如何消除？

uint64_t request_size = ele_cnt * (uint64_t)ele_size;
if(request_size != (size_t) request_size)
    /*overflow must have occurred ,Abort operation */
    return NULL;
void *result = malloc(request_size);
if(result == NULL)
    /*malloc failed*/
    return NULL;

2.3.6 乘以常数

以往，在大多数机器上，整数乘法指令相当慢，需要10个或者更多的时钟周期，而其他整数运算（例如加法、减法、位级运算和移位）只需要1个时钟周期。即使在我们的参考机器Intel Core i7 Haswell 上，其整数乘法也需要3个时钟周期。因此，编译器使用了一项重要的优化，试着用移位和加法运算的组合来代替乘以常数因子的乘法。首先我们会考虑乘以2的幂的情况，然后在概括乘以任意常数。

原理：乘以2的幂。

设x为位模式 $\left [ x_{w-1},x_{w-2},...,x_{0} \right ]$ 表示的无符号整数。那么，对于任何 $k\geq 0$ ，我们都认为 $\left [ x_{w-1},x_{w-2},...,x_{0},0,...,0 \right ]$ 给出了 $x2^{k}$ 的 ω+k 位的无符号表示，这里右边增加了k个0.

因此，比如当ω=4时，11 可以被表示为[1011] 。k=2时，将其左移得到6位向量 [101100]，即可编码为无符号数11*4 = 44。

推导：乘以2的幂。

$B2U_{w+k} \left ( \left [ x_{w-1},x_{w-2},...,x_{0},0,...0 \right ] \right ) =$ $\sum_{i=0}^{w-1}x_{i}2^{i+k}$

$= \left ( \sum_{i=0}^{w-1}x_{i}2^{i} \right ) * 2^{k}$

$=x2^{k}$

对其固定字长左移k位时，其高k位被丢弃，得到

$\left [ x_{w-k-1},x_{w-k-2},...,x_{0},0,...,0 \right ]$

而执行固定字长的乘法也是这种情况。因此，我们可以看出左移一个数值等价于执行一个与2的幂相乘的无符号乘法。

原理：与2的幂相乘的无符号乘法。

C变量x和k有无符号数值x和k，且 $0\leq k< w$ ，则C表达式 $x\ll k$ 产生数值 $x * _{w}^{u}\textrm{}2^{k}$ 。

由于固定大小的补码算术运算和位级操作与其无符号运算等价，我们就可以对补码运算的2的幂的乘法与左移之间的关系进行类似的描述。

原理：与2的幂相乘的补码乘法。

C变量x和k有补码值x和无符号数值k，且 $0\leq k< w$ ，则C表达式 $x\ll k$ 产生数值 $x * _{w}^{u}\textrm{}2^{k}$ 。

注意，无论是无符号运算还是补码运算，乘以2的幂都可能会导致溢出。结果表明，即使溢出的时候，我们通过移位得到的结果也是一样的。回到前面的例子，我们将4为模式[1011]（数值为11）左移2位得到[101100]（数值为44）。将这个值截断为4位得到[1100]（数值为 12 = 44 mod 16）。

由于整数乘法比移位和加法的代价要多得多，许多C语言编译器试图以移位、加法和减法的组合来消除很多整数乘以常数的情况。例如，假设一个程序包含表达式x * 14 。利用 $14 = 2^{3} + 2^{2} +2^{1}$ ，编译器会将乘法重写为 $\left ( x \ll 3 \right ) + \left ( x \ll 2 \right ) + \left ( x \ll 1 \right )$ ，将一个乘法替换为3个移位和2个加法。无论x是无符号还是补码，甚至当乘法会导致溢出时，两个计算都会得到一样的结果。更好的是，编译器还可以利用属性 $14 = 2^{4}-2^{1}$ ，将乘法重写为 $\left ( x \ll 4 \right )-\left ( x \ll 1 \right )$ ，这时只需要2个移位和1个减法。

例题2.38 LEA指令能够执行如 $\left ( a\ll k \right ) + b$ 的计算，这里k等于0、1、2或3，而b等于0或者某个程序值。编译器常常用这条指令来执行常数因子乘法。例如，我们可以用 $\left ( a\ll 1 \right ) +a$ 来计算 $3*a$ 。

考虑b等于0或者等于a、k为任意可能的值的情况，用一条LEA指令可以计算a的哪些倍数？

根据公式得出最后结果为 $2^{k}$ 或 $2^{k} + 1$ ，1、2、3、4、5、8、9 倍。

2.3.7 除以2的幂

在大多数机器上，整数除法要比整数乘法更慢——需要30个或者更多的时钟周期。除以2的幂也可以用移位运算来实现，只不过我们用的是右移，而不是左移。无符号和补码数分别使用逻辑一位和算术移位来达到目的。

整数除法总是舍入到零。为了精确定义，我们需要引入一些符号。

对于任何实数a，定义 $\left \lfloor a \right \rfloor$ 为唯一的整数 $a^{'}$ ，使得 $a^{'} \leq a < a^{'} +1$ 。例如， $\left \lfloor 3.14 \right \rfloor = 3$ ， $\left \lfloor- 3.14 \right \rfloor = -4$ ，而 $\left \lfloor 3\right \rfloor = 3$ 。

同样，定义 $\left \lceil a \right \rceil$ 为唯一整数 $a^{'}$ ，使得 $a^{'} -1 < a \leq a^{'}$ 。例如， $\left \lfloor 3.14 \right \rfloor = 4$ ， $\left \lfloor- 3.14 \right \rfloor = -3$ ，而 $\left \lfloor 3\right \rfloor = 3$ 。

对于 $x \geq 0 , y > 0$ ，结果会是 $\left \lfloor x/y \right \rfloor$ ，而对于 $x < 0,y>0$ 结果会是 $\left \lceil x/y \right \rceil$ ，也就是说，它将向下舍入一个正值，而向上舍入一个负值。

对于无符号运算使用移位是非常简单的，部分原因是由于无符号数的右移一定是逻辑右移。

原理：除以2的幂的无符号除法。

C变量x和k有无符号数值x和k，且 $0\leq k< w$ ，则C表达式 $x \gg k$ 产生数值 $\left \lfloor x/2^{k} \right \rfloor$ 。

k	$\gg k$ （二进制）	十进制	$12340/2^{k}$
0	0011000000110100	12340	12340.0
1	0001100000011010	6170	6170.0
4	*0000*001100000011	771	771.25
8	*00000000*00110000	48	48.203125

推导：除以2的幂的无符号除法。

设x为位模式 $\left [ x_{w-1},x_{w-2},...,x_{0} \right ]$ 表示的无符号整数，而k的取值范围为 $0\leq k< w$ 。设 $w^{'}$ 为 $w-k$ 位位表示 $\left [ x_{w-1},x_{w-2},...,x_{k} \right ]$ 的无符号数，而 $x^{''}$ 为k位位表示 $\left [ x_{k-1},x_{k-2},...,x_{0} \right ]$ 的无符号数。由此，我们可以看到 $x=2^{k}x^{'}+x^{''}$ ，而 $0\leq x^{''}< 2^{k}$ ，因此可得到 $\left \lfloor x/2^{k} \right \rfloor = x^{'}$ 。

对位向量 $\left [ x_{w-1},x_{w-2},...,x_{0} \right ]$ 逻辑右移k位会得到位向量

$\left [0,...0, x_{w-1},x_{w-2},...,x_{k} \right ]$

这个位向量有数值 $x^{'}$ ，我们看到，该值可以通过计算 $x\gg k$ 得到。

对除以2的幂的补码运算来说，情况要稍微复杂一点。首先，为了确保负数仍然是负数，移位要执行的是算术右移。现在让我们来看看这种右移会产生什么情况。

原理：除以2的幂的补码除法，向下舍入。

C变量x和k分别由补码值x和无符号数值k，且 $0\leq k< w$ ，则当执行算术移位时，C表达式 $x\gg k$ 产生数值 $\left \lfloor x/2^{k} \right \rfloor$

对于 $x\geq 0$ ，变量x的最高有效位为0，所以移位的效果与逻辑右移是一样的。因此，对于非负数来说，算术右移k位于除以 $2^{k}$ 是一样的。作为一个负数的例子，图2-29 给出了对 -12340的16位表示进行算术右移不同位数的结果。对于不需要舍入的情况（k=1），结果是 $x/2^{k}$ 。但是当需要进行舍入时，移位导致的结果向下舍入。例如，右移4位会吧-771.25向下舍入为-772。我们需要调整策略来处理负数x的除法。

2-29 补码算术右移
k	$\gg k$ （二进制）	十进制	$-12340/2^{k}$
0	1100111111001100	-12340	-12340.0
1	1110011111100110	-6170	-6170.0
4	1111110011111100	-772	-771.25
8	1111111111001111	-49	-48.203125

推导：除以2的幂的补码除法，向下舍入。

设x为位模式 $\left [ x_{w-1},x_{w-2},...,x_{0} \right ]$ 表示的补码整数，而k的取值范围为 $0\leq k< w$ 。设 $x^{'}$ 为 $w-k$ 位 $\left [ x_{w-1},x_{w-2},...,x_{k} \right ]$ 表示的补码数，而 $x^{''}$ 为低k位 $\left [ x_{k-1},x_{k-2},...,x_{0} \right ]$ 表示的无符号数。通过与对无符号情况类似的分析，我们有 $x=2^{k}x^{'}+x^{''}$ ，而 $0\leq x^{''}< 2^{k}$ ，得到 $x^{'} = \left \lfloor x/2^{k} \right \rfloor$ 。进一步，我们可以观察到，算术右移位向量 $\left [ x_{w-1},x_{w-2},...,x_{0} \right ]$ k位，得到位向量

$\left [x_{w-1},...,x_{w-1}, x_{w-1},x_{w-2},...,x_{0} \right ]$

他刚好是将 $\left [ x_{w-1},x_{w-2},...,x_{k} \right ]$ 从 $w-k$ 位符号扩展到ω位。因此，找个移位后的位向量就是 $\left \lfloor x/2^{k} \right \rfloor$ 的补码表示。

原理：除以2的幂的补码除法，向上舍入。

C变量x和k分别由补码值x和无符号值k，且 $0\leq k< w$ ，则当执行算术移位时，C表达式 $\left ( x+\left ( 1\ll k \right ) -1 \right ) \gg k$ 产生数值 $\left \lceil x/2^{k} \right \rceil$

图2-30说明在执行算术右移之前加上一个适当的偏置量是如何导致结果正确舍入的。在第三列，我们给出了-12340加上偏量值之后的结果，低k位（那些会向右移出的位）以斜体表示。我们可以看到，低k位左边的位可能会加1，也可能不会加1。对于不需要舍入的情况（k=1），加上偏置量只影响那些被移掉的位，对于需要舍入的情况，加上偏量导致较高的位加1，所以结果会向零舍入。

2-30 补码除以2的幂（右移之前加上偏量，结果向零舍入）
k	偏量	-12345+偏量	$\gg k$ （二进制）	十进制	$-12340/2^{k}$
0	0	1100111111001100	1100111111001100	-12340	-12340.0
1	1	1100111111001101	1110011111100110	-6170	-6170.0
4	15	1100111111011011	1111110011111100	-771	-771.25
8	255	1101000011001011	1111111111001111	-48	-48.203125

偏置技术利用如下属性：对于整数x和y（y>0）， $\left \lceil x/y \right \rceil = \left \lfloor \left ( x+y-1 \right )/y \right \rfloor$ 。例如，当x=-30和y=4，我们有 x+y-1 = -27，而 $\left \lceil -30/4 \right \rceil = -7 = \left \lfloor -27/4 \right \rfloor$ 。当x=-32和y=4时，我们有x+y-1 = -29 ，而 $\left \lceil -32/4 \right \rceil = -8 = \left \lfloor -29/4 \right \rfloor$ 。

推导：除以2的幂的补码除法，向上舍入。

查看 $\left \lceil x/y \right \rceil = \left \lfloor \left ( x+y-1 \right )/y \right \rfloor$ ，假设 x=qy+r，其中 $0\leq r< y$ ,得到 $\left ( x+y-1 \right )/y = q+\left ( r+y-1 \right )/y$ ，因此 $\left \lfloor \left ( x+y-1 \right )/y \right \rfloor = q + \left \lfloor \left ( r+y-1 \right )/y \right \rfloor$ 。当r=0时，后面一项等于0，而当r>0时，等于1，也就是说，通过给x增加一个偏量y-1，然后再将除法向下舍入，当y整除x时，我们得到q，否则，就得到q+1。

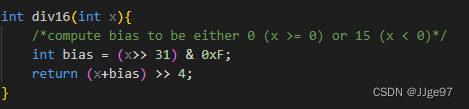
例题2.42 写一个函数div16，对于整数参数x返回x/16的值。你的函数不能使用除法、模运算、乘法、任何条件语句、任何比较运算符或任何循环。假设数据类型int 为32位长，使用补码表示，而右移是算术右移。

例题2.43 在下面的代码中，我们省略了常数M和N的定义：

#define M /*Mystery number 1*/
#define N /*Mystery number 2*/
int arith(int x,int y){
    int result = 0;
    result = x*M+y/N; /* M and N are mystery numbers*/
    return result;
}

我们以某个M和N的值编译了这段代码。编译器用我们讨论过的方法优化乘法和除法。下面将产出的机器代码翻译回C语言的结果。

/* translation of assembly code for arith*/
int optarith(int x,int y){
    int t = x;
    x <<= 5;
    x -= t;
    if(y<0) y+=7;
    y >>=3; /*Arithmetic shift*/
    return x+y;
}

请问M和N的值为多少。

解：按照乘法公式 $\left ( x\ll \left ( n+1 \right ) \right ) - \left ( x\ll m \right )$ 解析 $x =$ $\left ( x \ll 5 \right ) -x$

$M = 2^{5} - 2^{0} = 31$

N为8 因为，当y为非负数时右移3位。当y<0时，偏置量为7；

2.3.8 关于整数运算的最后思考

我们看到的，计算机执行的“整数”运算实际上就是一种模运算形式。表示数字的有限字长限制了可能的值的取值范围，结果运算可能溢出。我们还看到，补码表示提供了一种既能表示负数也能表示正数的灵活方法，同时使用了与执行无符号算术相同的位级实现，这些运算包括加法、减法、乘法，甚至除法，无论运算数是以无符号形式还是以补码形式表示的，都有完全一样或者非常类似的位级行为。

例题2.44 假设我们在对有符号值使用补码运算的32位机器上运行代码。对于有符号值使用的是算数右移，而对无符号值使用的是逻辑右移。变量的声明和初始化如下：

int x = foo();/* Arbitrary value*/
int y = bar();/* Arbitrary value*/

unsigned ux = x;
unsigned uy = y;

对于下面每个C表达式：

证明对于所有的x和y值，它都为真（等于1）；
给出使得它为假（等于0）的x和y值；

( x>0 ) || ( x-1<0 );
( x & 7 ) != 7 || ( x<< 29 <0);
( x*x) >=0;
x<0 || -x <= 0;
x>0 || -x >= 0;
x+y == uy+ux;
x*~y + uy *ux == -x;

JJge97

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
深入理解计算机系统(CSAPP):第二章.信息的表示和处理

深入理解计算机（csapp）第二章第三小节，主要讲述整数的运算在计算机底层操作。
复制链接

扫一扫

专栏目录

深入理解计算机系统(CSAPP):第二章.信息的表示和处理

2.3 整数运算

2.3.1 无符号加法

2.3.2 补码加法

2.3.3 补码的非

2.3.4 无符号乘法

2.3.5 补码乘法

2.3.6 乘以常数

2.3.7 除以2的幂

2.3.8 关于整数运算的最后思考

“相关推荐”对你有帮助么？