2023年CSP-J复赛真题解析

2023年CSP-J-T1-小苹果（apple）

题目描述

小Y的桌子上放着n个苹果从左到右排成一列，编号为从1到n。

小苞是小Y的好朋友，每天她都会从中拿走一些苹果。

每天在拿的时候，小苞都是从左侧第1个苹果开始、每隔2个苹果拿走1个苹果。

随后小苞会将剩下的苹果按原先的顺序重新排成一列。

小苞想知道，多少天能拿完所有的苹果，而编号为n的苹果是在第几天被拿走的？

输入格式

从文件apple.in中读入数据。

输入的第一行包含一个正整数，表示苹果的总数。

输出格式

输出到文件apple.out中。

输出一行包含两个正整数，两个整数之间由一个空格隔开，分别表示小苞拿走所有苹果所需的天数以及拿走编号为n的苹果是在第几天。

输入输出样例

输入样例1：

8

输出样例1：

5 5

说明

样例1解释：

小苞的桌上一共放了8个苹果。

小苞第一天拿走了编号为1、4、7的苹果。

小苞第二天拿走了编号为2、6的苹果。

小苞第三天拿走了编号为3的苹果。

小苞第四天拿走了编号为5的苹果。

小苞第五天拿走了编号为8的苹果。

数据范围：

对于所有测试数据有：1 ≤ n ≤ 10^9。

特殊性质：小苞第一天就取走编号为n的苹果。

耗时限制1000ms   内存限制512MB

解析

考点：数学

90 分解法：

类似约瑟夫问题的模拟去标记处理，对于 90% 的测试数据，n≤10^6，开一个 10^6\数组即可做标记。然后循环处理标记数组，因为每一轮都会去掉 1/3 的苹果。因此最多循环 log3/2​10^6 次。

思路分析：

找规律的题。题目有两问：

1. 苹果什么时候拿完？
2. 编号为 n 的苹果是在第几轮被拿走的？

对于第一问，容易发现，按拿走的规则看，每三个苹果就会拿走一个苹果。因此，每一轮拿走的苹果数量是⌈n/3⌉。也就是每次都至少拿走三分之一的苹果。如此，我们可以直接循环修改 n 并计数，就可以在 O(log2/3​​n) 时间复杂度下求出第一问。

对于第二问，容易发现，编号为 n 的苹果只要在当前一轮中没有被拿走，那么在下一轮中，它仍旧是最后一个苹果。对于 n 号苹果，如果它所在的位置 mod3 为 1，那么就会被拿走。因此，我们在第一问的循环修改中直接判断 n 即可确定 n 号苹果是在第几轮被拿走的。

时间复杂度：O(log2/3​​n)

参考代码：

#include<bits/stdc++.h>
using namespace std;

int n, day, ans;

int main(){
    cin >> n;
    int m = n;  // 当前苹果数量
    while(m) {  // n 号苹果在每一轮都是最后一个苹果，也就是第 m 个苹果
        day++;
        if(m%3==1 && !ans) ans = day; // n 号个苹果在这一天被拿走
        m -= (m+3-1)/3;  // 向上取整
    }
    cout << day << ' ' << ans;
    return 0;
}

2023年CSP-J-T2-J 公路（road）

题目描述

小苞准备开着车沿着公路自驾。

公路上一共有 n 个站点，编号为从 1 到 n。 其中站点i与站点 i + 1 的距离为vi公里。

公路上每个站点都可以加油，编号为 i 的站点一升油的价格为ai元，且每个站点只出售整数升的油。

小苞想从站点 1 开车到站点 n，一开始小苞在站点 1 且车的油箱是空的。已知车的油箱足够大，可以装下任意多的油，且每升油可以让车前进d公里。

问小苞从站点 1 开到站点 n，至少要花多少钱加油？

输入格式

从文件road.in中读入数据。

输入的第一行包含两个正整数 n 和 d, 分别表示公路上站点的数量和车每升油可以前进的距离。

输入的第二行包含 n - 1 个正整数v1, v2 . . . vn-1,分别表示站点间的距离。

输入的第三行包含n个正整数 a1, a2. ... an, 分别表示在不同站点加油的价格。

输出格式

输出到文件road.out中。

输出一行，仅包含一个正整数，表示从站点1开到站点，小苞至少要花多少钱加油。

输入输出样例

输入样例1：

5 4 
10 10 10 10 
9 8 9 6 5

输出样例1：

79

说明

【样例1解释】

最优方案下：小苞在站点1买了3升油，在站点2购买了5升油，在站点4购买

了2升油。

【数据范围】

对于所有测试数据保证：1 ≤ n ≤ 10^5，1 ≤ d ≤ 10^5，1 ≤ vi ≤ 10^5，1 ≤ ai ≤10^5。

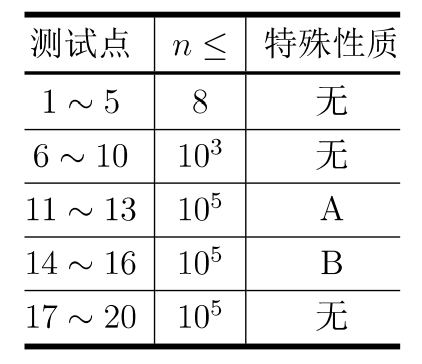
特殊性质A: 站点1的油价最低。

特殊性质B: 对于所有 1 ≤ i < n, vi 为 d 的倍数。

耗时限制1000ms   内存限制512MB

解析

考点：贪心

由于油箱容量无限大，因此容易发现，从 i 号站点走到 i+1 号站点这一段路，我们需要的油可以从前 i 个站点去购买。其实就相当于在i 号站点买油需要花费的代价是前 i 个站点买油所需要的最小值。

接下来，我们就按照刚才这个性质进行模拟每次从当前站点买够刚好能走到下一个站点的油就可以了。

实现时，要注意，由于必须购买整数升的汽油，因此跑到一个新站点后汽油是可能有剩余的，因此要注意保存剩余能跑的里程数。

参考代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+5;
in