算法和数据结构解析-10 : 二叉树及递归问题

1.数和二叉树数据结构

1.1 树（Tree）

树是一种非线性的数据结构，是由n（n >=0）个结点组成的有限集合。

如果n==0，树为空树。如果n>0，树有一个特定的结点，叫做根结点（root）。根结点只有直接后继，没有直接前驱。

除根结点以外的其他结点划分为m（m>=0）个互不相交的有限集合，T0，T1，T2，...，Tm-1，每个集合都是一棵树，称为根结点的子树（sub tree）。

下面是一些其它基本概念：

1. 节点的度：节点拥有的子树个数
2. 叶子节点（leaf）：度为0的节点，也就是没有子树的节点
3. 树的高度：树中节点的最大层数，也叫做树的深度

1.2 二叉树（Binary Tree）

对于树这种数据结构，使用最频繁的是二叉树。

每个节点最多只有2个子节点的树，叫做二叉树。二叉树中，每个节点的子节点作为根的两个子树，一般叫做节点的左子树和右子树。

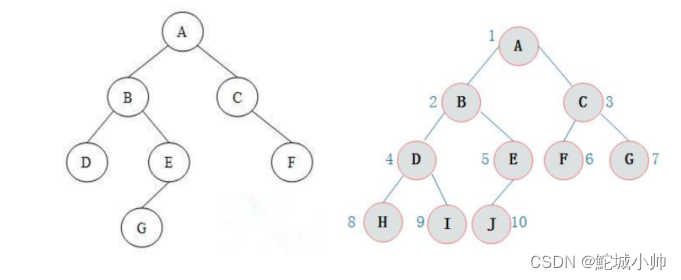
（1）二叉树的性质

二叉树有以下性质：

1. 若二叉树的层次从0开始，则在二叉树的第i层至多有2^i个结点(i>=0)
2. 高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)(空树的高度为-1)
3. 对任何一棵二叉树，如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1

（2）满二叉树和完全二叉树

1. 满二叉树：除了叶子节点外，每个节点都有两个子节点，每一层都被完全填充。
2. 完全二叉树：除了最后一层外，每一层都被完全填充，并且最后一层所有节点保持向左对齐。

1.3 递归（Recursion）

对于树结构的遍历和处理，最为常用的代码结构就是递归（Recursion）。

递归是一种重要的编程技术，该方法用来让一个函数（方法）从其内部调用其自身。一个含直接或间接调用本函数语句的函数，被称之为递归函数。

递归的实现有两个必要条件：

1. 必须定义一个“基准条件”，也就是递归终止的条件。在这种情况下，可以直接返回结果，无需继续递归
2. 在方法中通过调用自身，向着基准情况前进

一个简单示例就是计算阶乘：0 的阶乘被特别地定义为 1；n的阶乘可以通过计算 n-1的阶乘再乘以n来求得的。

public class Recursion {
    // 递归示例：计算阶乘
    public static int factorial(int n){
        if (n == 0)return 1;
        return factorial(n-1) * n;
    }

    // 尾递归计算阶乘，需要多一个参数保存“计算状态”
    public static int factorial2(int acc, int n){

        if (n == 0)return acc;
        return factorial2(acc * n,n-1) ;
    }
}

上面的第二种实现，把递归调用置于函数的末尾，即正好在return语句之前，这种形式的递归被称为尾递归 (tail recursion)，其形式相当于循环。一些语言的编译器对于尾递归可以进行优化，节约递归调用的栈资源。

1.4 二叉树的遍历

• 中序遍历：即左-根-右遍历，对于给定的二叉树根，寻找其左子树；对于其左子树的根，再去寻找其左子树；递归遍历，直到寻找最左边的节点i，其必然为叶子，然后遍历i的父节点，再遍历i的兄弟节点。随着递归的逐渐出栈，最终完成遍历
• 先序遍历：即根-左-右遍历
• 后序遍历：即左-右-根遍历
• 层序遍历：按照从上到下、从左到右的顺序，逐层遍历所有节点。

定义TreeNode(树节点):

package com.webcode.binary_tree;
// 二叉树的节点类
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x){
        val = x;
    }
}

用递归可以很容易地实现二叉树的先序、中序、后序遍历：

    // 1. 先序遍历
    public static void printTreePreOrder(TreeNode root){
        // 处理基准情形
        if (root == null) return;

        System.out.print(root.val + "\t");    // 先打印根
        printTreePreOrder(root.left);     // 打印左子树
        printTreePreOrder(root.right);    // 打印右子树
    }

    // 2. 中序遍历
    public static void printTreeInOrder(TreeNode root){
        // 处理基准情形
        if (root == null) return;

        printTreeInOrder(root.left);     // 打印左子树
        System.out.print(root.val + "\t");    // 打印根
        printTreeInOrder(root.right);    // 打印右子树
    }

    // 3. 后序遍历
    public static void printTreePostOrder(TreeNode root){
        // 处理基准情形
        if (root == null) return;

        printTreePostOrder(root.left);     // 打印左子树
        printTreePostOrder(root.right);    // 打印右子树
        System.out.print(root.val + "\t");    // 打印根
    }

层序遍历，则需要借助一个队列：要访问的节点全部放到队列里。当访问一个节点时，就让它的子节点入队，依次访问。

    // 4. 分层遍历
    public static void printTreeLevelOrder(TreeNode root){
        // 定义一个队列
        LinkedList<TreeNode> queue = new LinkedList<>();

        // 先把根节点放入队列
        queue.offer(root);

        // 只要队列不为空，就一直出队
        while (!queue.isEmpty()){
            TreeNode curNode = queue.poll();
            System.out.print(curNode.val + "\t");

            // 将子节点加入队列
            if ( curNode.left != null )
                queue.offer(curNode.left);
            if ( curNode.right != null )
                queue.offer(curNode.right);
        }
    }

1.5 二叉搜索树（Binary Search Tree）

二叉搜索树也称为有序二叉查找树，满足二叉查找树的一般性质，是指一棵空树具有如下性质：

• 任意节点左子树如果不为空，则左子树中节点的值均小于根节点的值
• 任意节点右子树如果不为空，则右子树中节点的值均大于根节点的值
• 任意节点的左右子树，也分别是二叉搜索树
• 没有键值相等的节点

 基于二叉搜索树的这种特点，在查找某个节点的时候，可以采取类似于二分查找的思想，快速找到某个节点。n 个节点的二叉查找树，正常的情况下，查找的时间复杂度为 O(logN)。

二叉搜索树的局限性

一个二叉搜索树是由n个节点随机构成，所以，对于某些情况，二叉查找树会退化成一个有n个节点的线性链表。如下图:

1.6 平衡二叉搜索树（AVL树）

通过二叉搜索树的分析我们发现，二叉搜索树的节点查询、构造和删除性能，与树的高度相关，如果二叉搜索树能够更“平衡”一些，避免了树结构向线性结构的倾斜，则能够显著降低时间复杂度。

平衡二叉搜索树：简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树，根据科学家的英文名也称为AVL树。

它具有如下几个性质：

• 可以是空树
• 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过1

平衡的意思，就是向天平一样保持左右水平，即两边的分量大约相同。如定义，假如一棵树的左右子树的高度之差超过1，如左子树的树高为2，右子树的树高为0，子树树高差的绝对值为2就打破了这个平衡。

比如，依次插入1，2，3三个结点后，根结点的右子树树高减去左子树树高为2，树就失去了平衡。我们希望它能够变成更加平衡的样子。

AVL树是带有平衡条件的二叉搜索树，它是严格的平衡二叉树，平衡条件必须满足(所有节点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的。旋转的目的是为了降低树的高度，使其平衡。

使用场景

AVL树适合用于插入删除次数比较少，但查找多的情况。也在Windows进程地址空间管理中得到了使用。

1.7 红黑树（Red-Black Tree）

红黑树是一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

性质：

• 节点是红色或黑色
• 根节点是黑色
• 每个叶子节点都是黑色的空节点（NIL节点）。
• 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

在插入一个新节点时，默认将它涂为红色（这样可以不违背最后一条规则），然后进行旋转着色等操作，让新的树符合所有规则。

红黑树也是一种自平衡二叉查找树，可以认为是对AVL树的折中优化。

使用场景

红黑树多用于搜索,插入,删除操作多的情况下。红黑树应用比较广泛：

• 广泛用在各种语言的内置数据结构中。比如C++的STL中，map和set都是用红黑树实现的。Java中的TreeSet，TreeMap也都是用红黑树实现的。
• 著名的linux进程调度Completely Fair Scheduler，用红黑树管理进程控制块。
• epoll在内核中的实现，用红黑树管理事件块
• nginx中，用红黑树管理timer等

 1.8 B树（B-Tree）

 

B树(B-Tree)是一种自平衡的树，它是一种多路搜索树（并不是二叉的），能够保证数据有序。同时，B树还保证了在查找、插入、删除等操作时性能都能保持在O(logn)，为大块数据的读写操作做了优化，同时它也可以用来描述外部存储。

特点：

• 定义任意非叶子结点最多只有M个儿子；且M>2
• 根结点的儿子数为[2, M]
• 除根结点以外的非叶子结点的儿子数为[M/2, M]
• 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个key）
• 非叶子结点的关键字个数 = 指向儿子的指针个数 – 1
• 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]
• 非叶子结点的指针：P[1], P[2], …, P[M]，其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树
• 所有叶子结点位于同一层

                                                                     M = 3的B树

1.9 B+树

B+树是B-树的变体，也是一种多路搜索树。

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找。

B+的特性：

• 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的
• 不可能在非叶子结点命中
• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层
• 更适合文件索引系统

B+ 树的优点：

• 层级更低，IO 次数更少
• 每次都需要查询到叶子节点，查询性能稳定
• 叶子节点形成有序链表，范围查询方便。这使得B+树方便进行“扫库”，也是很多文件系统和数据库底层选用B+树的主要原因。

 2. 翻转二叉树

2.1 题目说明

翻转一棵二叉树。

示例：

输入： 

    4

   /   \

  2     7

 / \   / \

1   3  6   9

输出：

     4

   /   \

  7     2

 / \   / \

9   6  3   1

2.2 分析

这是一道很经典的二叉树问题。

显然，我们可以遍历这棵树，分别翻转左右子树，一层层递归调用，就可以翻转整个二叉树了。

2.3 方法一：先序遍历

容易想到，我们可以先考察根节点，把左右子树调换，然后再分别遍历左右子树、依次翻转每一部分就可以了。

这对应的遍历方式，就是先序遍历。

代码如下：

    // 1. 先序遍历
    public TreeNode invertTree1(TreeNode root){
        // 处理基准场景
        if (root == null) return null;

        // 1. 先处理根节点，交换左右子节点
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;

        // 2. 递归处理左右子树
        invertTree(root.left);
        invertTree(root.right);

        return root;
    }

复杂度分析

时间复杂度：O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。

空间复杂度：O(logN)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即O(logN)。而在最坏情况下，树形成链状，空间复杂度为O(N)。

2.4 方法二：后序遍历

类似地，我们也可以用后序遍历的思路：先递归地处理左右子树，然后再将左右子树调换就可以了。

代码如下：

    // 2. 后序遍历
    public TreeNode invertTree(TreeNode root){
        // 处理基准场景
        if (root == null) return null;

        // 1. 递归处理左右子树
        TreeNode left = invertTree(root.left);
        TreeNode right =  invertTree(root.right);

        // 2. 处理根节点，交换左右子节点
        root.left = right;
        root.right = left;

        return root;
    }

复杂度分析略，与方法一完全相同。

3.平衡二叉树

3.1 题目说明

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

• 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

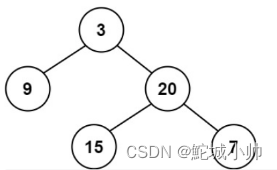
输入：root = [3,9,20,null,null,15,7]

输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]

输出：false

示例 3：

输入：root = []

输出：true

 3.2 分析

根据定义，当且仅当一棵二叉树的左右子树也都是平衡二叉树时，这棵二叉树是平衡二叉树。

因此可以使用递归的方式，判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下（类似先序遍历）或者自底向上（类似后序遍历）。

3.3 方法一：自顶向下

容易想到的一个方法是，从根节点开始，自顶向下递归地判断左右子树是否平衡。

具体过程是，先分别计算当前节点左右子树的高度，如果高度差不超过1，那么再递归地分别判断左右子树。这其实就是一个先序遍历的思路。

代码如下：

    // 方法一：先序遍历
    public boolean isBalanced1( TreeNode root ){
        if (root == null) return true;

        return Math.abs(height(root.left) - height(root.right)) <= 1
                && isBalanced1(root.left)
                && isBalanced1(root.right);
    }

    // 定义一个计算数高度的方法
    public int height(TreeNode root){
        if (root == null) return 0;
        return Math.max( height(root.left), height(root.right) ) + 1;
    }

复杂度分析

时间复杂度：O(n logn)，其中 n 是二叉树中的节点个数。

最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 O(n)。

对于节点 p，如果它的高度是 d，则计算高度的方法height(p) 最多会被调用 d 次（即遍历到它的每一个祖先节点时）。

对于平均的情况，一棵树的高度 h 满足 O(h)=O(logn)，因为d≤h，所以总时间复杂度为 O(nlogn)。对于最坏的情况，二叉树形成链式结构，高度为 O(n)，此时总时间复杂度为 O(n^2)。

空间复杂度：O(logn)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数平均为O(logn)，最坏情况为O( n)。

3.4 方法二：自底向上

上面的算法通过分析可以看到，每个节点高度的计算，会在它的祖先节点计算时重复调用，这显然是不必要的。

一种优化思路是，可以反过来，自底向上地遍历节点进行判断。计算每个节点的高度时，需要递归地处理左右子树；所以可以先判断左右子树是否平衡，计算出左右子树的高度，再判断当前节点是否平衡。这类似于后序遍历的思路。

这样，计算高度的方法height，对于每个节点就只调用一次了。

代码如下：

    // 方法二：后序遍历
    public boolean isBalanced( TreeNode root ){
        return balancedHeight(root) > -1;
    }

    // 定义一个直接判断当前数是否平衡的方法，也返回高度
    public int balancedHeight(TreeNode root){
        if (root == null) return 0;

        // 递归计算左右子树高度
        int leftHeight = balancedHeight(root.left);
        int rightHeight = balancedHeight(root.right);

        // 如果子树不平衡，直接返回-1
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1)
            return -1;

        // 如果平衡，返回当前高度
        return Math.max( leftHeight, rightHeight ) + 1;
    }

复杂度分析

时间复杂度： O(n)，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡，都只需要处理一次。最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O(n)。

空间复杂度： O(logn)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数平均为O(logn)，最坏情况为O( n)。

4. 验证二叉搜索树

4.1 题目说明

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:

    2

   / \

  1   3

输出: true

 示例 2:

输入:

    5

   / \

  1   4

     / \

    3   6

输出: false

解释: 输入为: [5,1,4,null,null,3,6]。

     根节点的值为 5 ，但是其右子节点值为 4 。

4.2 分析

按照二叉搜索树的性质，我们可以想到需要递归地进行判断。

这里需要注意的是，如果二叉搜索树的左右子树不为空，那么左子树中的所有节点，值都应该小于根节点；同样右子树中所有节点，值都大于根节点。

4.3 方法一：先序遍历

容易想到的方法是，用先序遍历的思路，自顶向下进行遍历。对于每一个节点，先判断它的左右子节点，和当前节点值是否符合大小关系；然后再递归地判断左子树和右子树。

这里需要注意，仅有当前的节点作为参数，做递归调用是不够的。

当前节点如果是父节点的左子节点，那么以它为根的子树所有节点值必须小于父节点；如果是右子节点，则以它为根的子树所有节点值必须大于父节点。所以我们在递归时，还应该把取值范围的“上下界”信息传入。

    // 方法一：先序遍历
    public boolean isValidBST1(TreeNode root){
        if (root == null) return true;

        return validator(root, null, null);
    }

    // 定义一个辅助校验器，用来传入上下界递归调用
    public boolean validator(TreeNode root, Integer lowerBound, Integer upperBound){
        if (root == null) return true;

        // 1. 判断当前节点的值是否在上下界范围内，如果超出直接返回false
        if (lowerBound != null && root.val <= lowerBound)
            return false;
        if (upperBound != null && root.val >= upperBound)
            return false;

        // 2. 递归判断左右子树
        return validator(root.left, lowerBound, root.val) && validator(root.right, root.val, upperBound);
    }

复杂度分析

时间复杂度 : O(n)，其中 n 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。

空间复杂度 : O(logn)，其中 nn 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度，平均情况为O(logn)。最坏情况下二叉树为一条链，树的高度为 n ，递归最深达到 n 层，故最坏情况下空间复杂度为 O(n)。

4.4 方法二：中序遍历

我们知道，对于二叉搜索树，左子树的节点的值均小于根节点的值，根节点的值均小于右子树的值。因此如果进行中序遍历，得到的序列一定是升序序列。

所以我们的判断其实很简单：进行中序遍历，然后判断是否每个值都大于前一个值就可以了。

    // 定义一个列表
    ArrayList<Integer> inOrderArray = new ArrayList<>();

    // 方法二：中序遍历
    public boolean isValidBST(TreeNode root){
        // 1.中序遍历，得到升序数组
        inOrder(root);

        // 2. 遍历数组，判断是否升序
        for (int i = 0; i < inOrderArray.size(); i++){
            if (i > 0 && inOrderArray.get(i) <= inOrderArray.get(i-1))
                return false;
        }

        return true;
    }

    // 实现一个中序遍历的方法
    public void inOrder(TreeNode root){
        if (root == null) return;

        inOrder(root.left);
        inOrderArray.add(root.val);
        inOrder(root.right);
    }

复杂度分析

时间复杂度 : O(n)，其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。

空间复杂度 : O(n)，其中 n 为二叉树的节点个数。用到了额外的数组来保存中序遍历的结果，因此需要额外的 O(n) 的空间。

4.5 方法三：用栈实现中序遍历

我们也可以不用递归，而使用栈来实现二叉树的中序遍历。

基本思路是：首先沿着左子树一直搜索，把路径上的所有左子节点压栈；然后依次弹栈，访问的顺序就变成自底向上了。弹栈之后，先处理当前节点，再迭代处理右子节点，就实现了中序遍历的过程。

public boolean isValidBST(TreeNode root) {

    Deque<TreeNode> stack = new LinkedList<>();

    double preValue = -Double.MAX_VALUE;

    // 遍历访问所有节点
    while ( root != null || !stack.isEmpty() ){

        // 迭代访问节点的左孩子，并入栈
        while ( root != null ){

            stack.push(root);
            root = root.left;

        }

        // 只要栈不为空，就弹出栈顶元素，依次处理
        if (!stack.isEmpty()){

            root = stack.pop();

            if ( root.val <= preValue )
                return false;

            preValue = root.val; 
            root = root.right;
        }
    }
    return true;
}

复杂度分析

时间复杂度 : O(n)，其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。

空间复杂度 : O(n)，其中 n 为二叉树的节点个数。栈最多存储 n 个节点，因此需要额外的 O(n) 的空间。