张量奇异值分解框架（tensor Singular Value Decomposition (t-SVD) framework）

最新推荐文章于 2025-03-17 23:46:20 发布

求求你不要出错啦

最新推荐文章于 2025-03-17 23:46:20 发布

阅读量5.5k

点赞数 7

文章标签：张量机器学习

本文链接：https://blog.csdn.net/weixin_42408308/article/details/116422925

版权

本文探讨了张量的一种替代表示形式，引入了张量的乘法运算，类似于矩阵的SVD分解，提出了张量的SVD框架（t-SVD）。t-SVD涉及新定义的张量乘法，张量转置，逆和正交张量概念，通过使用傅立叶变换优化计算。此外，文章介绍了t-SVD的数学基础，包括张量的Frobenius范数，以及如何将三阶张量分解为正交张量和f-diagonal张量的乘积。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

概述

传统上，使用CANDECOMP / PARAFAC（CP）或Tucker模型或其某些变体，将张量表示为1级外部乘积或将其分解。这样的分解是由特定的应用推动的，在这些特定的应用中，目标是找到给定多路阵列的近似这样的表示。近似表示的细节（例如，在和中使用多少项，正交性约束等）取决于应用程序。

在本文中，我们探索张量的替代表示形式。让人想起矩阵分解，我们提出了一个新的张量分解，将其作为张量的乘积。为了导出新的因式分解，我们定义了张量之间的闭合乘法运算。考虑这种新类型的张量乘法的主要动机是为张量设计新的因式分解，然后将其用于应用程序中。

具体地说，这种新的乘法使我们能够引入诸如张量转置，逆和恒等的概念，从而产生了正交张量的概念。乘法还产生线性运算符，并确定结果运算符的零空间。我们将向量的外部积的概念扩展到矩阵的外部积。所有推导均针对三阶张量给出。但是，它们可以很容易地扩展到p阶（p> 3）的情况。

张量背景以及记号

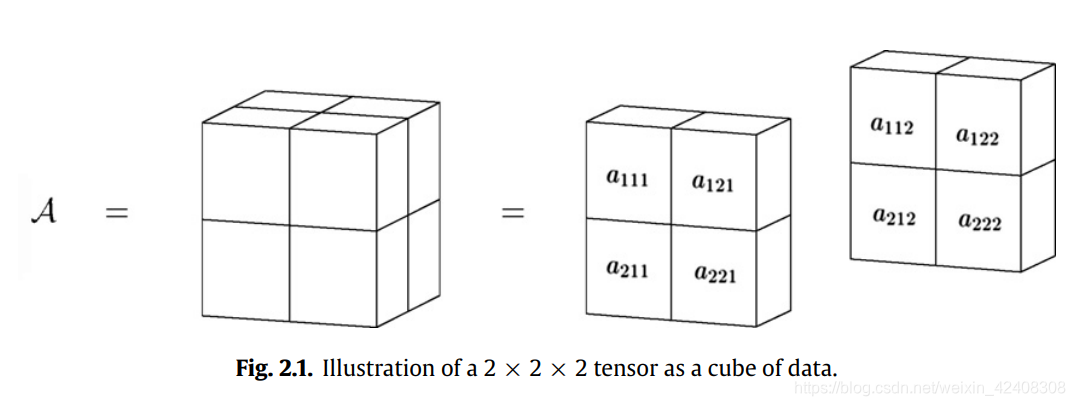
p阶张量： ${\color{Green} }\begin{equation} \mathcal{A}=\left(a_{i_{1} i_{2} \cdots i_{p}}\right) \in \mathbb{R}^{n_{1} \times n_{2} \times \cdots \times n_{p}} \end{equation}{\color{Green} }$

因此，矩阵被认为是二阶张量，向量是一阶张量。三阶张量可以表示为数据的“多维数据集”（见图2.1）

虽然三阶张量的方向不是唯一的，但引用其切片即通过将两个索引保持恒定而定义的二维截面很方便。横向和正面切片来指定哪些两个索引保持不变。使用Matlab表示法， $\begin{equation} \mathcal{A}(k,:,:) \end{equation}$ 对应于第k个水平切片， $\begin{equation} \mathcal{A}(:,k,:) \end{equation}$ 对应于第k个横向切片，而 $\begin{equation} \mathcal{A}(:,:,k) \end{equation}$ 对应于第k个正面切片。通过保持前两个索引不变并改变第三个索引来定义三阶张量的管。例如，使用Matlab表示法， $\begin{equation} \mathcal{A}(i,j,:) \end{equation}$ 是A的第ij个管。

在整个本文中，了解张量的方向至关重要。考虑到这一点，我们将限制在三阶张量上，并尽可能避免出现混乱的下标。因此，基于给定的方向，我们将主要指的是张量的前切片。

如果u是一个长度为m的向量，v是一个长度为n的向量，则 $\begin{equation} u \circ v \end{equation}$ 是u和v的外积。该外积给出一个秩为1的矩阵，其（i，j）项为由标量乘积 $\begin{equation} u_{i} v_{j} \end{equation}$ 决定。类似地，外部乘积 $\begin{equation} u \circ v \circ w \end{equation}$ 产生具有 $\begin{equation} u_{i} v_{j} w_{k} \end{equation}$ 给定的（i，j，k）项的秩为1的三阶张量。同样，四个向量的外积给出1阶，四阶张量等

p级张量A的张量秩r是表示张量所需的最小1秩张量。对于三阶张量 ${\color{Green} }\begin{equation} \mathcal{A} \in \mathbb{R}^{n_{1} \times n_{2} \times \cdots \times n_{p}} \end{equation}{\color{Green} }$ ，这意味着我们具有 $\begin{equation} \mathcal{A}=\sum_{i=1}^{r} \sigma_{i}\left(u^{(i)} \circ v^{(i)} \circ w^{(i)}\right) \end{equation}$ ------------------------(2.1)

其中σi是缩放常数。缩放常数只是r×r×r对角张量 $\begin{equation} \Sigma=\left(\sigma_{i j k}\right) \end{equation}$ 的非零元素（如果仅非零出现在元素 $\begin{equation} \sigma_{i j k} \end{equation}$ 中，其中i = j = k，则张量是对角线）。向量u（i），v（i）和w（i）分别是矩阵 $\begin{equation} U \in \mathbb{R}^{n_{1} \times r} \end{equation}$ ， $\begin{equation} V \in \mathbb{R}^{n_{2} \times r} \end{equation}$ ， $\begin{equation} W \in \mathbb{R}^{n_{3} \times r} \end{equation}$ 的第i列。

形式（2.1）的分解称为CANDECOMP–PARAFAC（CP）分解（CANonical DECOMPosition或PARAllel FACtors模型），无论r是否已知最小。注意，（2.1）中的矩阵U，V，W不限于正交。此外，形式（2.1）的正交分解位置可能不存在。没有已知的封闭形式解可以确定先验张量的秩r。张量的秩确定是一个广泛研究的问题。

HOSVD首先计算通过将各个维度上的张量“展平”而获得的矩阵的SVD，然后使用结果组装所谓的核心张量