已知两点坐标求水平距离_知道两个点的坐标X,Y，如何计算出两点间的距离以及角度，公式是什么...

展开全部

如果两个点的坐标参照系相同的话，对于同一平面内(即x、y相同Z相同)计算原理就按：两点坐e68a84e8a2ad62616964757a686964616f31333366303234标点X值之差的平方加Y值之差的平方后再开平方。如果不在同一平面内(即x、y相同Z不相同)，那么就是：两点坐标点X值之差的平方加Y值之差的平方再加Z值之差的平方后再开平方

假设A点坐标(x1,y1),B点坐标(x2,y2)

两点的距离为d

公式 d^2=(x2-x1)^2+(y2-y1)^2，求出d^2，然后开平方求出d了吧

角度

设直线AB的角度为C

tanC=(y2-y1)/(x2-1)，求出tanC，然后算tan的反函数就得到C了。

假设平面内任意两点X,Y，其坐标分别为X(a,b)、Y(c,d)，其中a≥c,d≥b . 则有以下关系式：

(XY两点距离)^2=(a-c)^2 +(d-b)^2 XY与水平方向的夹角θ(锐角)：tanθ=(d-b)/(a-c)。如X(6，4),Y(3，8) ，则(XY)^2=(6-3)^2+(8-4)^2 得XY=5 tanθ=(8-4)/(6-3)=4/3 得 θ=arctan4/3 ≈76.43°

扩展资料

公式

设两个点A、B以及坐标分别为

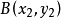 、  ，则A和B两点之间的距离为：

推论

直线上两点间的距离公式：

设直线  的方程为  ，点  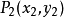，  为该线上任意两点，则

这一公式即所谓圆锥曲线的弦长公式。若记

 为直线AB的倾斜角，则

同时，若已知直线公式和其中一个点，并且给定了距离，可以反求另一个点的坐标。