皮尔逊相关系数 Pearson correlation coefficient

在统计学中，皮尔逊相关系数( Pearson correlation coefficient），又称皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，简称 PPMCC或PCCs），是用于度量两个变量X和Y之间的相关程度（线性相关），其值介于-1与1之间。

1 定义

两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商：

上式定义了总体相关系数，常用希腊小写字母作为代表符号。估算样本的协方差和标准差，可得到皮尔逊相关系数，常用英文小写字母 代表：

$r$ 亦可由 $(X_i,Y_i)$ 样本点的标准分数均值估计，得到与上式等价的表达式：

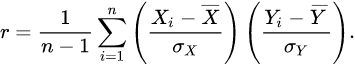
2 性质

总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上（计算样本皮尔逊系数的情况），或者双变量分布完全在直线上（计算总体皮尔逊系数的情况），则相关系数等于1或-1。皮尔逊系数是对称的：

皮尔逊相关系数有一个重要的数学特性是，因两个变量的位置和尺度的变化并不会引起该系数的改变，即它该变化的不变量(由符号确定)。也就是说，我们如果把 $X$ 移动到 $a+bX$，把 $Y$ 移动到 $c+dY$，其中a、b、c和d是常数，并不会改变两个变量的相关系数（该结论在总体和样本皮尔逊相关系数中都成立）。我们发现更一般的线性变换则会改变相关系数：

由于:

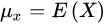
Y也类似，并且

故相关系数也可以表示成

对于样本皮尔逊相关系数：

3 物理意义

皮尔逊相关系数的变化范围为-1到1。 系数的值为1意味着X和Y可以很好的由直线方程来描述，所有的数据点都很好的落在一条直线上，且 $Y$ 随着 $X$ 的增加而增加。系数的值为−1意味着所有的数据点也都落在直线上，且 $Y$ 随着 $X$ 的增加而减少。系数的值为0意味着两个变量之间没有线性关系。

更一般的, 我们发现，当且仅当 $X_i$ 和 $Y_i$ 均落在他们各自的均值的同一侧， 则 $(X_i-\bar{X})(Y_i-\bar{Y})$ 的值为正。 也就是说，如果 和 同时趋向于大于，或同时趋向于小于他们各自的均值，则相关系数为正。 如果 和 趋向于落在他们均值的相反一侧，则相关系数为负。

3.1 皮尔森距离

通过皮尔森系数定义：

4 应用

主要讲一下在机器学习中的应用。

调包

from scipy.stats import pearsonr

4.1 衡量两个样本的相似度

在数据标准化 $(\mu =0,\sigma =1)$ 后，Pearson相关系数、Cosine相似度、欧式距离的平方可认为是等价的。换句话说，如果你的数据符合正态分布或者经过了标准化处理,那么这三种度量方法输出等价，不必纠结使用哪一种。

我们一般用欧式距离(向量间的距离)来衡量向量的相似度，但欧式距离无法考虑不同变量间取值的差异。举个例子,量a取值范围是0至1，而变量b的取值范围是0至10000，计算欧式距离时变量b上微小的差异就会决定运算结果。而Pearson相关系数可以看出是升级版的欧氏距离平方，因为它提供了对于变量取值范围不同的处理步骤。因此对不同变量间的取值范围没有要求(unit free)，最后得到的相关性所衡量的是趋势，可以克服不同变量量纲上的差别。

参考：
如何理解皮尔逊相关系数